电磁波在组合介质中传播的二维数值计算

严碧波 (长江大学电子信息学院,湖北荆州434023)

研究电磁波在介质中的衰减特性在许多领域中都有实际应用价值。目前被广泛应用的介质是吸波材料 (RAM),而近年来有关大气压下等离子体介质的吸波效应研究也显示其潜在应用前景。但这2种介质在电磁波衰减的机理上有着较大的差别。前者是由于电介质参数以及磁导率参数虚部的存在从而使得电磁波能量在其中传播时发生衰减;后者是由于被电磁波加速的电子通过与中性粒子发生碰撞而热化消耗电磁波能量。在对入射电磁波的吸收作理论描述时,这2种介质对电磁波的响应也是不一样的。对吸波材料可以通过在麦克斯韦方程组中对介电常数和磁导率添加适当的虚部 (耗散项)来进行描述,这在传统的时域有限差分 (FDTD)算法中已有成熟的算例[1～4]。而对电磁波在大气等离子中传播,由于等离子体中的电子处于非束缚状态,它们对外加电磁场的响应与中性粒子有很大的不同,必须将麦克斯韦方程组与电子流体的运动方程耦合求解才能正确地描述。对一维 (电磁波正入射到等离子体层)问题,通过求解波动方程或者直接由麦克斯韦方程组以及耦合电子的运动方程进行差分求解[5,6];也可采用解析的方法即几何光学近似方法求解[7,8]。对于二维 (电磁波斜入射到等离子体层)问题,也可采用几何光学近似方法求解,但这种方法在电子密度梯度较大时,由于几何光学近似的前提条件得不到保证,只能通过数值方法对麦克斯韦方程组与电子流体运动方程的耦合方程进行数值求解[9,10]。

上述2种介质在不同的应用环境中有不同的优缺点,适当地把这2种介质进行组合,探讨不同的组合参数对电磁波衰减的影响,这对有效地提高吸波特性有着重要的参考价值。笔者以由大气等离子体层、吸波材料层和金属层组成的组合介质为研究对象 (以下统称为组合介质),通过数值计算模拟,研究在给定入射波频率时,反射波的衰减与等离子体的电子密度剖面、等离子体厚度、入射电磁波的偏振模式与入射角之间的关系。为了计算的一致性与方便,无论对于电磁波在等离子体层中的传播,还是在吸波材料中传播,都采用时域有限差分 (FDTD)算法来进行数值求解。

1 数值方法

对电磁波在等离子体中传播的FDTD计算,因为电磁波在大气压下的等离子体中传播,电磁波电场强度 (或者是磁场强度)的振幅有可能在1个波长范围内或者在1个周期范围内变化很大,这样电磁波的场量函数不再是1个周期性函数,所以需要采用给出全时域的全波解才能正确描述电磁波在等离子体中的传播行为。为此,需要对电子流体方程直接进行离散差分。另外,根据FDTD算法的基本思想[1,2],对TM波方程,将电场与磁场强度在空间节点上交错抽样 (相差半个空间步长),在时间节点上相差半个时间步长,2个方向上的磁场强度空间节点也交错抽样,这样TM波耦合方程组的差分格式可以表示如下:

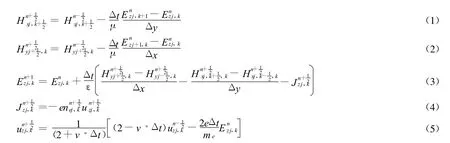
式中,Hx、Hy分别为X、Y轴方向上的磁场强度;Jz、uz、Ez分别为Z轴方向上的电流密度分量、电子流体速度分量、电场分量;V表示电子与中性粒子的碰撞频率;n为时间取样;j、k为空间网格点取样;ne、e、me分别为电子密度、电子电量、电子质量。

TM波与TE波有着对偶关系[1],因此TM波和TE波方程可统一编程计算。电磁波在吸波材料中传播的方程求解可直接采用FDTD的差分公式进行计算[1]。

2 数值模拟

组合材料的数值模拟可以统一的采用FDTD算法,在不同材料的衔接地方,其各个参数的选取在FDTD算法中都有相应的处理方法[2],不同介质区域采用不同的介质参数,其结构如图1所示。

组合介质对电磁波的衰减与等离子体层参数、吸波材料层参数以及入射电磁波参数均紧密相关,所涉及的参数包括等离子体的电子密度剖面、电子与中性粒子碰撞频率ve0(GHz)、等离子体厚度d1(mm)、电磁波的入射角 θ(°)、电磁波入射波频率 f(GHz)、电磁波传播模式 (TM波和T E波)、吸波材料介电参数及其空间分布、吸波材料的厚度d2(mm)。其中金属层厚度d3取2.5mm。

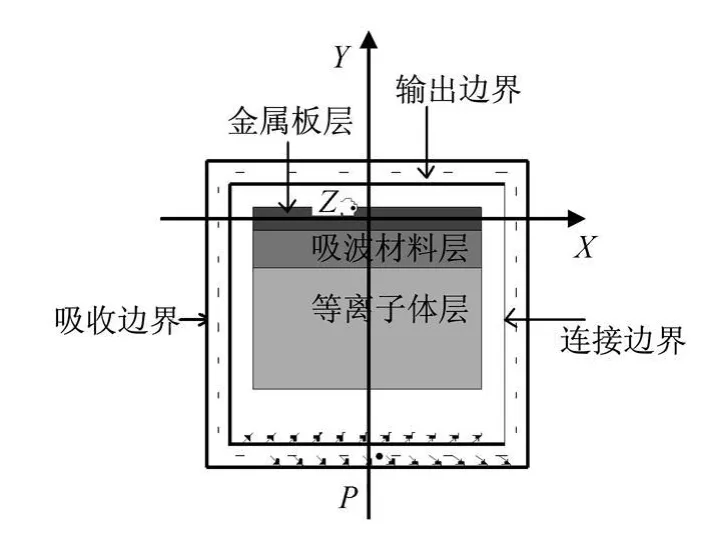
图1 FDTD计算域示意图

2.1 入射角与极化模式对衰减特性的影响

入射角对衰减特性的影响主要通过以下3个方面:①角度变化影响电磁波在有耗介质中穿行距离的变化。很显然角度越大,电磁波在介质中穿行距离也越大;②极化模式的影响与入射角的大小关系密切,在0°入射角时TM波与TE波是等价的[9],随着角度的增加,极化模式影响也相应增加。③入射角的变化对介质直接反射波的影响。如图2所示,随着角度的增加,电磁波在等离子体层中的反射率(RdB)减小。图3表示TM波和TE波在入射角发生变化时组合介质的衰减特性。从计算结果来看,在每种极化模式中,随着入射角的变化,等离子体对反射波的衰减影响较大,因为等离子体层厚度较大(20mm)而吸波层较小 (6.25mm)。因此角度变化使得电磁波在等离子体层中穿行距离的变化比电磁波在吸波层中穿行距离变化要显著的多。另外从计算结果来看,随着角度的增加 (小于45°),电磁波的极化模式对衰减特性的影响在增加,同时TE波的衰减性能 (dB)要好于TM波,并且角度越大,这2种模式衰减性能的差异就越大。

2.2 电子密度剖面对衰减特性的影响

组合介质的反射波由3种反射波组成,即等离子体反射、吸波材料的反射和金属层的反射。要使得组合介质有较好的衰减特性,首先要求等离子体层反射波尽量小。在图3中,低频率端衰减特性较差,这很大程度上是由于在低频率端双曲正切电子密度剖面对入射波直接反射较大的缘故。因此,在最大电子密度一定的条件下,等离子体的电子密度剖面对等离子体的反射率影响很大。笔者选用了几种电子密度剖面,如图4所示。从图5可以看到指数、线性和半钟形在低频率段的衰减特性得到较好的改善,指数剖面在开始段梯度最小,而后上升较快,因此总衰减特性受吸波材料的影响较大,但整体衰减特性最差,这是因为该电子密度剖面平均电子密度最小。

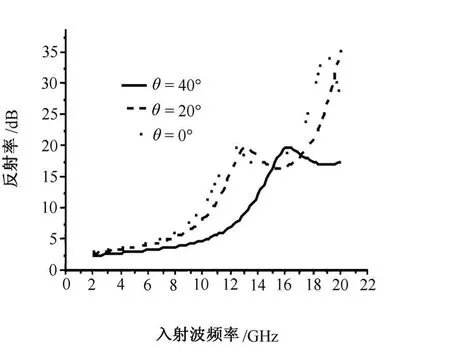
图2 入射角对等离子体层反射波的影响

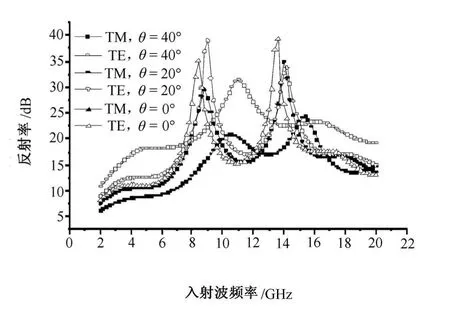
图3 入射角对电滋波衰减的影响

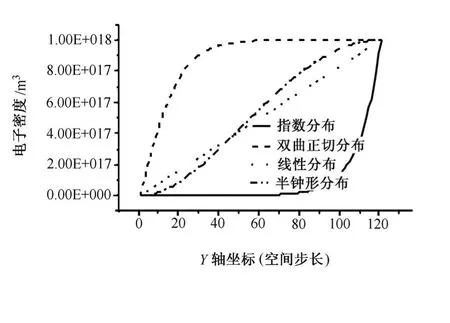
图4 几种电子密度剖面

2.3 等离子体和吸波材料的厚度对衰减特性的影响

如图6和图7计算结果所示,当电子密度剖面一定时 (如双曲正切),厚度的改变引起了3种反射波振幅的大小与相位的改变,相对于等离子体,吸波材料的反射波衰减曲线中峰值的位置与大小发生了较为明显的变化。在组合介质中,由于每种介质材料在参数适当情况下均有较好的吸波特性,因此在图示的范围内单一地改变一种介质的厚度对总衰减特性影响不大。

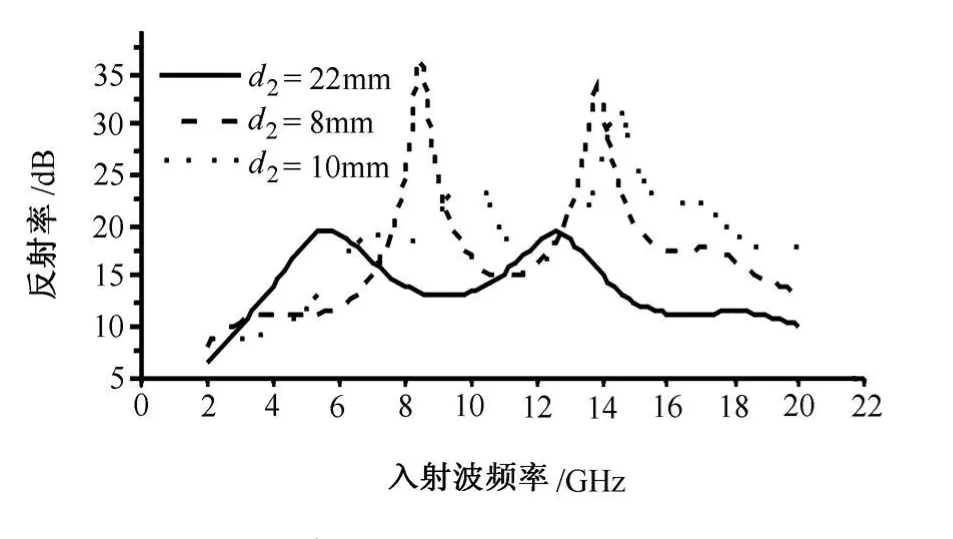
图6 吸波材料厚度(d2)对电磁波衰减的影响

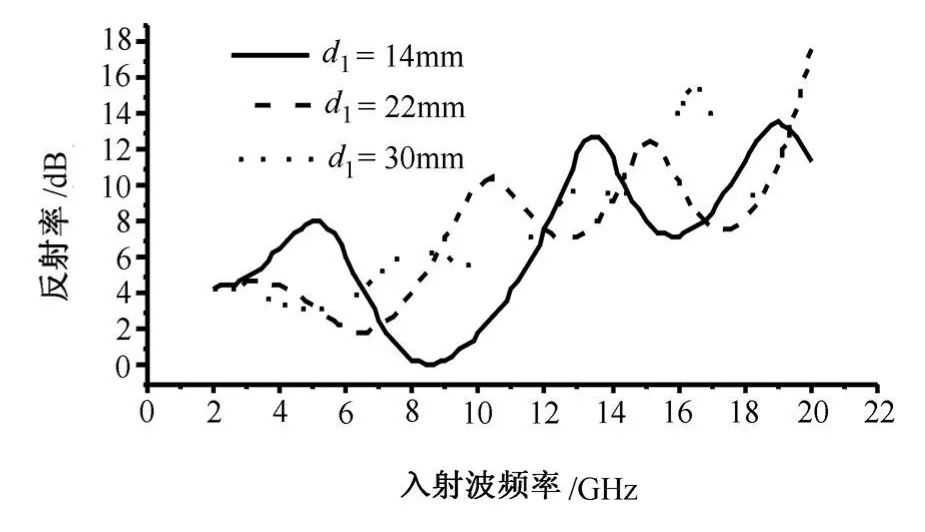
图7 等离子体厚度对电滋波衰减的影响

3 结 语

应用FDTD算法对由等离子体、吸波材料和金属层组成的组合介质的电磁波衰减特性进行了数值模拟。计算结果表明,在吸波材料参数给定的情况下,组合介质的反射波衰减特性与电磁波的极化模式、等离子体的密度剖面、电磁波的入射角、等离子体厚度和吸波材料的厚度等紧密相关。在入射角足够大的情形下,电磁波极化模式对衰减特性的影响较大。

[1]葛德彪,闫玉波.电磁波时域有限差分方法 [M].西安:电子科技大学出版社,2002.

[2]Taflove A.Computational Electrodynamics:the Finite-Difference-Time-Domain Method[M].Boston:Artech House,1995.

[3]刘少斌,莫锦军,袁乃昌.各向异性磁化等离子体JEC-FDTD算法 [J].物理学报,2004,(53):783～787.

[4]葛德彪,吴跃丽,朱湘琴.等离子体散射FDTD分析的移位算子方法 [J].电波科学学报,2003,18(8):359～363.

[5]Hu X W,Liu M H.Propagation of an Electromagnetic Wave in a Mixing of Plasma-dense Neutral Gas[J].Plasma Science&Technology,2004,6(6):2564～2566.

[6]Liu M H,Hu X W,Jiang Z H,et al.Finite-Difference Time-Domain Analysis of Wave Propagation in a Thin Plasma Layer[J].Chin Phy s Lett,2006,(23):410～413.

[7]莫锦军,刘少斌,袁乃昌.非均匀等离子体覆盖目标隐身研究[J].电波科学学报,2002,17(1):69～73.

[8]袁敬闳,莫怀德.等离子体中的波 [M].成都:电子科技大学出版社,1990.

[9]Jiang Z H,Hu X W,Liu M H,et al.Propagation of Electromag netic T M(S-Polarization)Mode in T wo Dimensional Atmospheric Plasma[J].Science&T echnology,2006,(8):297～299.

[10]Jiang Z H,Hu X W,Liu M H,et al.Propagation of a Scatttered Electromagnetic Wave With P-Polarization(TE)Mode in Atmospheric Plasma[J].Chin Phys Lett,2006,(23):1238～1240.