GM(1，1)等维新息模型在某市需水量预测中的应用

2010-04-15赵东亮

山西建筑 2010年22期

王波赵东亮

0 引言

常用的需水量预测方法主要有模糊神经网络法、时间序列法、数理统计方法等，应用这些方法建立模型，通常需要长序列的原始数据资料，而实际上往往达不到这一要求。而邓聚龙先生创立的灰色预测方法对时间序列短、信息不完全、统计数据少的建模与分析具有独特的功能，能够有效的解决这一问题。它可以不去考虑相关影响因素，直接从原始数据系列寻找数据内在的相关规律，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测未来发展趋势的状况[2]。

1 GM(1，1)等维新息模型的理论与建模步骤

所谓等维新息，是指用GM(1，1)模型预测一个值，而后将这个预测值补充在已知数列之后，同时去掉最老的一个数据，保持数列等维，再建立GM(1，1)模型预测下一个值，将其结果再补充到数列之后，再去掉最老的一个数据这样新陈代谢，逐个预测，依次递补，直到完成预测目标或达到一定精度为止。这样，在整个预测过程中模型参数是在不断变化的。采用等维新息建立的GM(1，1)模型，充分利用了预测所得到的新信息，缩小了灰平面的范围，有效的提高了预测的精度[3，4]。

1.1 GM(1，1)等维新息模型的建模步骤

GM(1，1)模型是 GM(1，N)中，当 N=1时的特例，建立GM(1，1)模型只需一个数列 X(0):

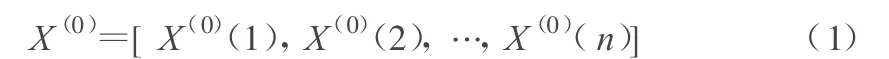
对 X(1)做一次累加生成(1-AGO)，生成数据序列 X(1):

利用序列X(1)可建立如下白化方程:

求出 a，u后，解式(4)得微分方程:

对式(6)进行如下还原生成，可得X(0)(k)的模拟值为:

经检验模型合格后，可以将预测出的新数据 X(0)(k)加入到原始序列中，同时去掉最老的信息X(0)(1)，用新的数据序列再次建立GM(1，1)模型，保证数列等维，并检验，依次反复，直至完成预测目标，这样就可以把精度相对较高的数据和新出现的扰动因素及时考虑到模型中，突出最新的变化趋势，同时，去掉了对输出影响越来越小的陈旧信息，从而提高预测的精度[5，6]。

1.2 精度校验

通常采用后验差方法对模型的精度进行检验[7，8]。模型精度由均方差比值和小误差概率共同评定。精度检验要求均方差比值越小越好，小误差概率越大越好。设 e为残差，S21，S22为原始序列X(0)及残差序列e的均方差，则后验差比计算公式为:

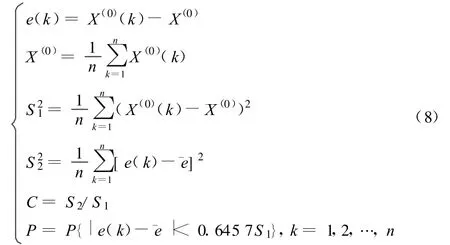
其中，C为后验差比值;P为小误差概率。

模型精度级别=max{C所处级别，P所处级别}。

2 应用实例

2.1 孟州市基本情况

孟州市地处东经 112°33′～ 112°55′，北纬 34°50′～ 35°02′，系太行山前丘陵向黄河冲积平原过渡地区，地势西北高，东南低，海拔高度108.5 m～307.9 m，相对高差199.4 m。全市辖 8镇3乡2个办事处，269个行政村，98 911个农户，总人口 356 889人，总面积541 km2。现有耕地35.93万亩，粮食作物以小麦、玉米为主，经济作物有棉花。森林覆盖率为4.6%。

孟州市属暖温带大陆性季风型气候，四季分明。全年平均日照时数 2 405.9 h，年平均太阳辐射总量 122.3 kcal/cm2，年平均气温14.2℃。年平均降雨量598.5 mm，最多年份1 014.3 mm，最少年份340.4 mm，无霜期209 d。

2.2 需水量预测

2.2.1 数据预处理

由于原始数据序列为等时距序列，因此不必进行处理(如果原始数据序列为不等时距序列，可采用Lagrange插值多项式分别进行分段插值计算，得到等时距序列)。

2.2.2 最佳模型维数的确定

利用孟州市1995年～2004年的城市需水量数据资料，分别以1995年～2004年(10维)，1996年～2004年(9维)，1997年～2004年(8维)，…，2002年～2004年(3维)的用水量数据构建GM(1，1)等维新息模型 3维到模型 10维，不同维数的预测效果见表1。

从表1可以看出，当模型的维数为7维时，预测精度最高，2005年的相对误差为-7.28%，2006年的相对误差仅为-5.56%，2005年和2006年的平均预报误差为-6.42%。根据后验差检验结果可知，模型的等级均为一级，满足精度要求，因此选择7维的GM(1，1)等维新息模型作为孟州市需水量预测模型。

2.2.3 模型预测精度校验