基于罚函数的滑行艇阻力性能优化方法研究*

许蕴蕾

(海军驻上海地区舰艇设计研究军事代表室 上海 200011)

基于罚函数的滑行艇阻力性能优化方法研究*

许蕴蕾

(海军驻上海地区舰艇设计研究军事代表室 上海 200011)

滑行艇;阻力;罚函数;优化方法

滑行艇的阻力性能优化是设计滑行艇艇体的重要内容之一,如何减小艇体阻力是设计师优先考虑的目标。文章从传统的SIT阻力估算方法着手,分析滑行艇受到的力和力矩,并引入Savitsky对艇体阻力的修正,即考虑因喷溅而产生的摩擦阻力。由于滑行艇的重心纵向位置对阻力性能有很大影响,故通过构造罚函数法,把有约束问题化为无约束问题,利用MATLAB优化工具箱中的fm incon函数计算出最佳的重心纵向位置。最后,通过某滑行艇模型的水池拖曳试验验证了该优化方法的可行性,具有一定的工程参考价值。

0 引 言

滑行艇水动力性能的研究历来是研究的难点,其中重要的一项内容是对阻力性能的研究。阻力是船舶最重要的性能之一,如果能从理论上设计出最小阻力船型,这将为整个船舶设计周期节省大量的劳力,时间和费用。随着“时间”价值的不断提高,人们对各种运输工具速度的要求也日益提高。对民用船舶来说,航速的提高意味着货物周转周期的缩短以及经济效益的提高;对军用舰艇来说则意味着战斗力的增强[1]。

滑行艇阻力性能优化主要包括艇体型线优化、艇体参数优化和添加附体等。艇体型线优化通常可以应用数学方法对型线进行光顺,但是必须以艇体的布置、水动力与结构性能的要求为目标函数。在以艇体阻力性能为型线优化对象时,只能在某些约束条件下完成[2]。海军工程大学船舶与海洋工程系与水动力学国家重点实验室,通过对三种艇型及不同喷气方式的模型试验,研究了断阶滑行艇模型气层减阻的实施途径及减阻效果,取得了总阻力减少25%以上的结果,提出了一种适合于采用气层减阻技术且阻力性能优良的艇型[3]。崔焰、卢晓平对方尾水面舰船,采用Hohrop阻力计算公式,以总阻力为目标函数,据遗传算法,对主要的船型参数进行了优化计算[4]。滑行艇的重心纵向位置对阻力性能有很大影响。从减小阻力考虑,重心后移是有利的,它对应较大的有利宽度,使滑行效率提高;但对避免海豚运动发生和波浪中的运动响应和冲击力都会带来不利影响。因此,如何确定艇体的重心纵向位置是设计滑行艇阻力性能的重要内容之一。

1 SIT阻力估算方法

SIT法又称Savitsky法[5],它是根据美国史蒂文斯实验室水池试验结果提出的。自1964年Savitsky提出该方法以来,已有几种不同的版本,即使Savitsky版也是Krovkin-Kroukovsky和Murray等人研究工作的延续和修改。以多种形式出现的SIT法可能是在美国应用得最多的滑行艇阻力预报方法。不同的版本常给出不同的结果,不过,它们的核心却是相同的。该方法认为动浮力与攻角不应该是线性关系,而是经滑行参数表示的升力、扭矩方程(以压力中心函数的形式)。

1.1 Savitsky的力和力矩方程

滑行艇的阻力包括压差阻力Rp(或称剩余阻力)和摩擦阻力Rf两大部分。压差阻力又包括飞溅阻力和兴波阻力,它们分别等于动水力压力合力P和静水压力P0在运动方向的分量;而P和P0在铅锤方向的分量之和等于艇重。因此可知压差阻力与艇重的关系为:

滑行艇的阻力:

一般地,倾角较小(cosτ≈1),艇底来流速度近似地取等于航速,这样R为倾角τ和湿长度l的函数,欲确定τ和l,可以通过滑行艇运动时的受力及力矩平衡方程来求解。

不计推力与摩擦力的铅垂分量及这些力对尾缘点的力矩,并考虑到小攻角的条件,得出铅垂方向力的平衡方程和对尾缘点力矩的平衡方程:

式中:lG——重心至尾缘距离(沿龙骨方向);

Mp——动压力合力对尾缘的力矩;

Mp0——静压力合力对尾缘的力矩。

SIT法的无因次力平衡方程

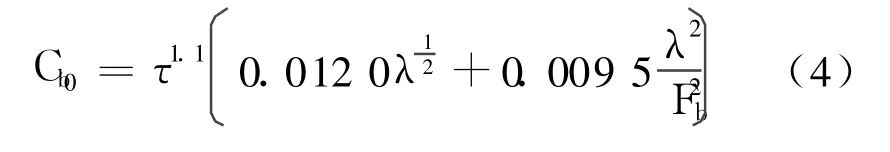
式中:第一项为无因次动浮力项,第二项为无因次静浮力项;倾角的单位为“°”。当有横倾角时,需要进行以下修正:

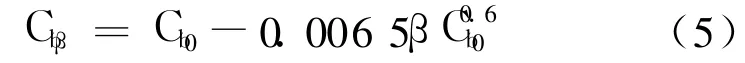
SIT法的无因次力矩平衡方程,以压力中心的方式表达:

式中:

为求解λ和τ,可采用如下计算步骤:

1)已知滑行艇排水量Δ、航速V、艇宽b和斜升角β,计算宽度傅汝德数Fb及艇的实际负载系数

由(5)式可以求得相当平板的动负荷系数Cb0。

2)令lp=lG,则(6)式可转化为:

3)联立式(4)、(8),采用拟牛顿法编程求解这一非线性方程组。

1.2 喷溅阻力

1964年的Savitsky版本中未考虑喷溅引起的湿面积对摩擦阻力的影响。2006年,Savitsky重新修改了1964年版本,使其能够计及喷溅引起的湿面积所产生的摩擦阻力。湿面积由两部分组成:湿底压力区和喷溅区。滑行艇动升力完全由湿底压力区提供,喷溅区只产生摩擦阻力[7]。

当滑行艇高速滑行时,由于受到流体动力作用,出现有明显的飞溅现象,艇底流动模型如图1所示。在两舷侧形成一种连续喷射的圆锥面水膜,称为膜状飞溅或主飞溅;此外,在驻点线前还有向两舷外侧喷射的,由很细小的水滴组成的水流束,称为须状飞溅。这两种飞溅损耗的能量就产生飞溅阻力,而须状飞溅还将增加艇底浸湿面积,以致对摩擦阻力有所影响。由于喷溅速度难以测量,喷溅层还不同于常规边界层,常规边界层不能用于准确求解喷溅对摩擦阻力的影响,这造成喷溅对总阻力的影响难以准确确定。

图1 艇底流动模型

在滑行状态下,喷溅基线同驻点线的纵向距离非常小,如图1所示,在喷溅基线处的水流速度沿驻点线的方向。目前,估算船体总粘性阻力时,以喷溅基线后的面积作为总的湿面积。

图1中,被驻点线OC、浸湿龙骨(长度为Lk)、两条浸湿舭缘线(长度为LC),以及尾端围成的两块区域为底部压力区域Ap、As为喷溅区域面积,喷溅区域的大小同斜升角β和纵倾角τ有关。对于棱柱型船,Savitsky给出了浸湿长度同斜升角以及纵倾角之间的关系:

Bowles和Denny给出了预测滑行艇艏部附近的水表面扰动模型公式:

因水动压力产生的喷溅,同船体构型(如舭部升高、纵倾以及舭部湿/干的区域)和工作条件(如滑行艇的速度和所受的自由表面波浪)和成比例关系。因此,采用经验公式来确定喷溅阻力:

其中K1由滑行艇的速度决定,它有以下关系:

喷溅处的压力由下面的公式进行计算:

其中P为喷溅基线处的压力,系数K2可近似确定为:

其中b(y)是喷溅处距纵中剖面的距离,如图2所示:

图2 喷溅基线处压力系数的确定

因而喷溅所产生的喷溅阻力和升力可用以下公式进行计算:

1.3 总阻力

考虑到喷溅引起的湿面积对摩擦阻力的影响,滑行艇实际受到的阻力应再加上喷溅引起的摩擦阻力Rsp,则滑行艇总阻力表示为:

(15)式中的排水量通常已知,而攻角τ未知。在摩擦阻力Rf中,压力区浸湿面积未知,它取决于浸湿长度;喷溅引起的摩擦阻力Rsp也与浸湿长度有关,而浸湿长度是随艇体排水量、航速、艇宽、重心纵向位置和斜升角的变化而变化的。

一般来说,根据任务书来设计滑行艇的阻力性能,其艇体排水量、艇宽、最高航速、巡航速度通常都已经确定,可以改变的是重心纵向位置和斜升角。而如何确定最佳的重心纵向位置和斜升角,以达到滑行艇在最高航速和巡航速度具有较小的功率,则是本文的研究目标。

2 罚函数的艇体阻力优化方法

2.1 基本原理

罚函数法即序列无约束极小化方法,它的基本原理是将有约束问题化为无约束问题,亦即将原来的目标函数和约束函数,按一定方式构成一个新的函数,当这个新的函数向函数逼近,它的最优解也就是原问题的最优解。罚函数法又分为:内点罚函数法,外点罚函数法和混合罚函数法[6]。

2.2 优化目标

在艇型优化之前,需要明确滑行艇阻力性能设计的目标,即在巡航速度和最高航速时,阻力较小。从发动机有效功率来看,优化目标可以定义为:滑行艇在最高速度航行时的有效功率与巡航速度时的有效功率之比最小,并且以最高速度航行时的有效功率尽可能小。

2.3 设计变量

如前所述,影响滑行艇阻力的几个主要要素为:排水量Δ、艇宽B、航速V、重心纵向位置lG和斜升角β。由于艇宽和排水量受到设计指标的限定,这里均设为定值。

2.4 目标函数

由修正后的SIT预报模型(15)式可知:

假设滑行艇巡航速度和最高航速分别为V1、V2,则优化的目标函数为:

引入中间变量τ1,τ2,λ1,λ2,上式可写作:

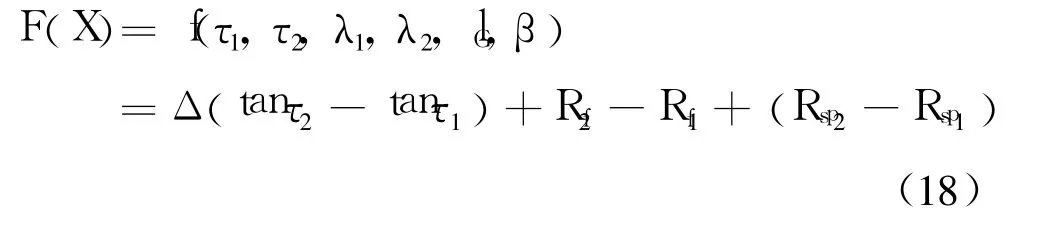
2.5 约束函数

(1)由SIT法的无因次力平衡方程得

(2)对于相当平板的动负荷系数Cb0有

(3)由SIT法的无因次力矩平衡方程得

(4)当攻角＞12°时,已非滑行状态了,故有

(5)斜升角≤30°

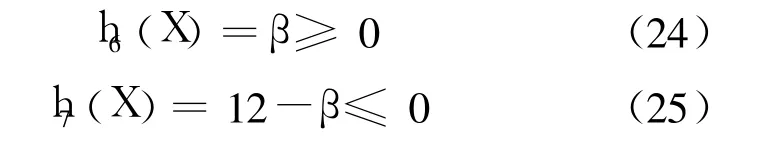
(6)重心位置应处在艇中之后,以艇中靠后3%～4%艇长L(折角线长)为最佳[6]。

在(1)、(2)、(3)、(5)之条件下,和约束条件完全相同,故一共有15组。

2.6 优化计算

本文滑行艇的阻力性能优化模型属于非线性约束的最优化问题,采用SQP算法。因此,这里可以使用MATLAB优化工具箱中的fmincon函数[8]。MATLAB中SQP法的实现分3步,即:

(1)拉格朗日函数Hess矩阵的更新;

(2)二次规划问题求解;

(3)一维搜索和目标函数的计算。

3 基于模型艇的计算实例

根据上述罚函数的滑行艇阻力优化方法,对某滑行艇模型进行优化计算,其模型参数如表1所示,通过母型船换算得到的巡航速度和最高航速分别为6.0 m/s、10.0m/s。首先,在MATLAB程序中是建立目标函数的m文件,即编写目标函数程序并保存在objfun.m文件中;然后建立非线性约束条件的m文件并保存在confun.m文件中;最后编写优化程序。程序执行过程是通过优化程序中的fmincon函数调用目标函数和约束条件函数,并用表1中的各种参数作为优化初始值实现优化运算。通过MATLAB程序优化模型的计算,可得到最佳的重心纵向位置lG=0.71m,即重心距船舯后0.39m。

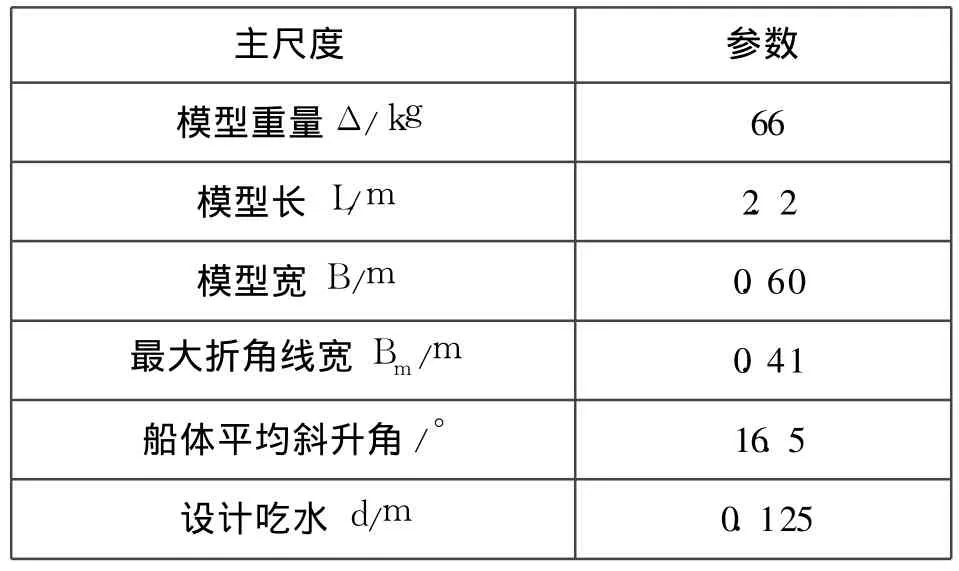
表1 某滑行艇船模参数

3.1 模型的水池拖曳试验验证

为了确定艇体各种参数对滑行艇阻力性能的影响,在某所高速水动力试验室进行了船模的水池拖曳试验,通过测试该模型不同的重量、重心位置、附体等情况下的阻力、升沉、纵倾角等参数,从而为滑行艇的艇型改进和实艇的设计提供技术依据。该模型为木质,表面打磨光滑、喷漆,经检验符合“滑行艇船模阻力试验方法(CB/Z 244-88)”中的允差标准。模型主要参数如表1所示。

为了确定艇体重心位置对滑行艇阻力性能的影响,分别进行重心距船舯后350 mm、370 mm、390 mm的水池拖曳试验,对测量的阻力制成图表如图3所示:

由图3可知,当Vm＜5.0m/s时,艇体重心距船舯后Xgm=350 mm的模型阻力较小;当Vm＞5.0 m/s以后,Xgm=390 mm的模型阻力较小,阻力减小最大处达2.78%左右。这说明在相同排水量下,滑行艇开始滑行后,艇体重心后移将使纵倾角增大、湿表面积减小,阻力减小。

图3 不同重心纵向位置的阻力变化曲线

4 结 语

本文根据Savitsky的阻力估算方法分析了滑行艇受到的力和力矩,并在总阻力中计入喷溅引起的摩擦阻力;通过利用罚函数的优化方法,确定了阻力优化的目标,设计了优化变量、目标函数和约束函数,然后利用MATLAB优化工具箱中的fmincon函数对艇体阻力进行优化计算,得出最佳的艇体重心纵向位置,并通过某滑行艇的模型水池拖拽试验验证了该方法的可行性。

[1] 董祖舜.快艇动力学[M].武汉:华中理工大学出版社,1994.

[2] 黄金森.基于最小阻力的船型优化研究[D].天津大学工学硕士学位论文,2005.12.

[3] 董文才,郭日修,陈小玲,吕岩松.滑行艇气层减阻试验[J].中国造船,2002,43(4).

[4] 崔焰,卢晓平.基于Holtrop公式与遗传算法的船型参数优化[J].海军工程大学学报,2009,21(6):26-29.[5] 董文才,郭日修.滑行艇阻力研究进展[J].船舶力学,2000,4(4):68-81.

[6] 朱凯.滑行艇的型线优化设计及性能分析[D].哈尔滨工程大学工学硕士学位论文,2007.

[7] 孙华伟.三体滑行艇船型与快速性研究[D].哈尔滨:哈尔滨工程大学硕士论文,2010.1

[8] 褚洪生,杜增吉,阎金华等编著.MATLAB7.2优化设计实例指导教程[M].机械工业出版社,2007:91-119.

Optimization on Resistance Capability of Planing Craft Based on Penalty Function

Xu Yunlei

planing craft;resistance;penalty function;optimization

Resistance capability optimization is one of the important issues to design a planing craft hull,and the top-priority aim for designer is how to reduce the hull resistance.Firstly,the SIT resistance estimation method is introduced,and the force and moment on planning craft are analyzed,then the Savitsky modification of hull resistance is proposed,namely the frictional resistance caused by spray.Due to the great effect of the barycenter position to resistance capability,the penalty function is implemented to change the constrained problem to unconstrained problem.The best barycenter position is calculated by the fmincon function in the MATLAB optimized kit.Finally,the feasibility of the optimization method is validated by the tank daggle trial of a planing craft model.

U 661.33

A

1001-9855(2010)05-0009-05

2010-06-25

许蕴蕾(1981.06-),女,汉族,吉林人,助理工程师,主要从事船舶设计审查工作。