受非完整性约束的移动机器人路径跟踪算法

郁 伉， 肖本贤， 李艳红

(1.合肥工业大学电气与自动化工程学院，安徽合肥 230009;2.咸阳师范学院物理系，陕西咸阳 712000)

0 引 言

由于存在非完整约束，移动机器人路径跟踪控制十分具有挑战性。文献[1]对系统在期望路径附近Taylor线性化，对得到的线性时变系统设计控制律，从而实现原系统的局部跟踪;文献[2]采用输入输出反馈线性化的方法，将非线性系统分解为2个子系统，再根据性能指标逐一设计控制律，以达到跟踪目的;文献[3]采用后退(back steping)方法的思想，将系统分解为低阶系统，利用中间虚拟变量和部分Lyapunov函数，设计了具有全局渐进稳定的跟踪控制器。

目前常见机器人模型有运动学模型、动力学模型以及位姿误差模型。自文献[4]提出位姿误差模型以来，还很少见到新的模型。本文针对两轮差动驱动移动机器人，在仔细分析其工作过程的基础上，推导出新的模型，并给出2种算法。该模型在表达式上具有运动学模型简洁的优点，经过简单变换，得到1个运动周期内机器人位姿误差。2种算法针对机器人初始位置在期望路径附近，相对于传统的基于Lyapunov函数的控制律设计，不必计算大量偏导数，在保证跟踪精度、跟踪速度的前提下，具有计算量小的优点;和反馈线性化算法相比，不存在奇异性问题[5]。

1 定 义

机器人在t1时刻给定一个输入，紧接着在t2时刻给定另一个输入，则t2-t1即为机器人的运动周期T。由以上定义可知，在1个运动周期里，两轮差动驱动机器人的左轮线速度VL、右轮线速度V R保持不变。

若VL=VR，轨迹为直线段;若VL≠VR，轨迹为圆弧。假设机器人在平面上做纯滚动无滑动的运动，质心选取在两轮连线中心点上，机器人前进速度v、旋转角速度ω分别为:

其中，ω逆时针为正;D为两轮间距。

由(1)式解出VR、VL:

(2)式为两轮差动驱动机器人实际控制用的表达式，关键在于v、ω如何确定。

后面讨论的机器人，无特殊交代，都是指两轮差动驱动移动机器人，且设V SET为期望运动速度。

由前面分析，1个运动周期内，机器人轨迹只可能是直线段或圆弧，又因为直线段可以看成半径为∞的圆弧，因此模型中机器人轨迹以圆弧为例。假设某个运动周期开始，机器人位姿向量为(x0，y0，φ0)，结束时刻位姿向量为(x1，y1，φ1)。φ0、φ1是机器人前进方向与x轴正向夹角。

由图1可计算出圆心坐标(x0-R sinφ0，y0+R cosφ0)，R为圆弧半径。进而求得:

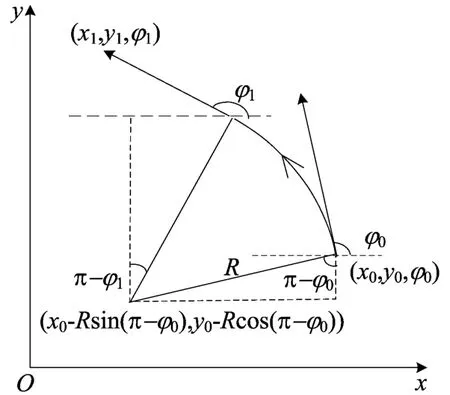
图1 运动周期模型

2 控制律提出

令Δx=x1-x0，Δy=y1-y0，代入(3)式得:

令k=Δy/Δx，Δx≠0。用(5)式除以(4)式得:

整理(6)式得:

解得:

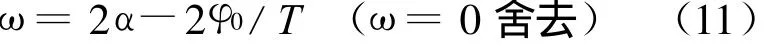
将(11)式代入(4)式得:

考虑到sin(2α-φ0)-sinφ0=2sin(α-φ0)cosα，则有:

(11)式和(12)式即为机器人路径跟踪控制律。关于如何选取Δx、Δy，将在后文重点介绍。

若期望路径是斜率为k的直线，并且机器人方向角沿着直线方向，即k=tanφ0。sinα=得α=φ0，代入(11)式得ω=0。代入(12)式得v=Δx/(T cosα)，这显然与实际情况相符合。

若Δx=0，即直线沿着y轴方向，若仍采用(11)式、(12)式控制律，则控制器奇异。可重新设k=Δx/Δy(Δy≠0)，具体推导公式同Δx≠0。因此，可根据运动方向定义k，避免奇异性问题。

该算法用到了移动机器人当前点和期望跟踪点2点之间的斜率，本文称其为斜率算法。

3 选取期望跟踪点

把跟踪点选取在期望路径上，是为了便于后续计算、分析、比较，同时也确保了机器人始终不会偏离期望路径太远。

设期望路径方程f(x)，机器人起始位姿向量(x0，y0，φ0)，运动周期结束时位姿向量即期望跟踪点位姿向量(x0+Δx，y0+Δy，φ0+ωT)。机器人轨迹方程(x-x r)2+(y-y r)2=R2，x r=x0-R sinφ0，yr=y0+R cosφ0，R=Δx/(2sin(α-φ0)cosα)，α是机器人起始点与期望跟踪点连线的倾斜角。由于跟踪点选取在期望路径上，Δy=f(x0+Δx)-f(x0)，关键在于Δx如何选取。

机器人在1个运动周期里前进的距离是V SET T，T是恒定的。显然，让机器人在每个运动周期里前进的距离一样，就可以让跟踪速度保持恒定，确保跟踪快速稳定，由此可建立等式(13):

y(x)是机器人实际轨迹。由于轨迹方程是二次微分方程，所以有2个解，y具体求解如图2所示。

图2 机器人运动轨迹

(13)式中被积函数和积分上限中都含有Δx，计算十分复杂，考虑到1个运动周期中，机器人起点、终点都在期望路径上，故Δy=f(x0+Δx)-f(x0)，有如下近似计算公式:

将f(x0+Δx)在x=x0处泰勒展开得:f(x0+Δx)=f(x0)+f′(x0)Δx+o(Δx)，并代入(14)式解得:

4 曲率半径算法

下面提出的算法用到了曲率半径的概念，称之为曲率半径算法。在1个运动周期里，移动机器人轨迹为圆弧，考虑到前进距离很短，且期望路径一般比较平滑，可认为曲率1/ρ不变，ρ为曲率半径。设移动机器人起点在期望路径上，方向角沿着圆弧切线方向，起点曲率半径为ρ。ρ即为运动周期模型中半径R，代入(4)式得:

解出:

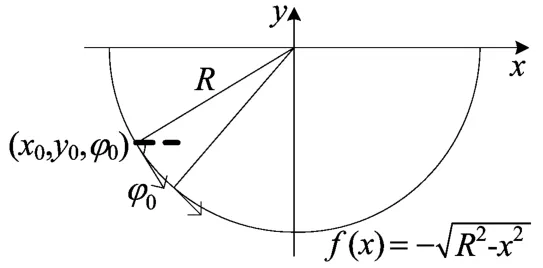
图3 期望路径为圆弧

令β=V SET T/R，代入(18)式:

继续化简:

将sin(β+φ0)=sinβcosφ0+cosβsinφ0，sinφ0=x0/R，cosφ0=-y0/R代入(21)式，有

当期望路径为圆弧时，Δx计算公式如(22)式。

由(17)式，欲求ω，先求出Δx/ρ+sinφ0:

将(23)式代入(17)式得:ω=β/T=V SET/R，由此v=VSET，与实际情况完全相符。

5 仿 真

首先定义跟踪误差e，如图4所示。直线x=xt，与期望路径相交于(xt，y f t)，与实际轨迹相交于(xt，yrt)。此时跟踪误差e为:

图4 跟踪误差定义

为了验证此模型和斜率算法的有效性，并且和现有的反馈线性化算法[5]做对比，在Matlab7.0上进行仿真实验。仿真参数见表1所列。

反馈线性化算法和斜率算法，可保证跟踪速度都恒为VSET，跟踪误差仿真结果如图5～图7所示。

表1 仿真参数

图6 斜率算法

图7 跟踪圆弧对比

在1个运动周期内，若e处处为零，则实际轨迹与期望路径完全重合。由于1个运动周期内，跟踪误差e有大有小，本次仿真中误差采样10次，取其平均值。让移动机器人跟踪直线y=x、圆弧抛物线y=x2、圆弧y=初始位置如下:图5a、图6a为(-1，-1.01，π/4);图5b、图6b为(-1，0，-π/2);图5c、图6c(-1，1，-1.107 1);图7a、图7b为(-0.099，0，-π/2);图7c为(-0.1，0，-π/2)。

由图5a、图5b、图6a、图6b可以看出，在跟踪直线和半径为1 m圆弧时，2种算法跟踪精度都能满足实际需求，误差在0.01 m以内，并且斜率算法不存在奇异性问题。由图5c、图6c可以看出，跟踪抛物线时，反馈线性化算法跟踪误差大于0.01 m，而斜率算法跟踪精度足以满足实际需求。

图5b、图6b跟踪圆弧半径r=1 m，图7a、7b跟踪圆弧半径r=0.1m。当圆弧半径减小时，反馈线性化算法跟踪精度急剧下降，而斜率算法跟踪精度提高2个数量级，并且误差波动很小。观察图6c，跟踪抛物线y=x2，在x=0附近，误差较小而此处曲率较大。圆弧半径越小，曲率越大。综上所述，斜率算法尤其适用于跟踪曲率较大的曲线。

对于期望路径是圆弧的特例，曲率半径算法仿真结果如图7c所示。由图7c可以看出，跟踪精度达10-17，并且进入稳态后，跟踪误差几乎为零。若初始条件和图7a、图7b一样，跟踪精度下降到10-3，但仍可以满足实际需求。跟踪精度下降，是因为推导曲率半径算法的前提中要求机器人初始位置在圆弧上，方向角沿着切线方向。

6 结束语

本文推导了两轮差动驱动移动机器人的一种实用模型，该模型关键在于找出一个运动周期内机器人起点坐标和终点坐标之间的关系，对于别的类型机器人建模也具有借鉴意义。最后通过仿真，验证模型、斜率算法和曲率半径算法的有效性，并且通过对比反馈线性化算法和斜率算法，验证了斜率算法的优越性。

仿真中大多假定机器人初始位置在期望路径上，若实际初始位置偏离期望路径太远，可以采用生成临时路径的办法[6]，并结合假设-预测-调整的迭代优化思想[7]、最大、最小蚂蚁系统的思想[8]，先让机器人运动到期望路径上，再采用本文的算法。减小算法对初始条件的依赖性，是下一步研究的方向。

[1] Walsh G，Tilbury D，Sastry S，etal.Stabilization of trajectories for systems w ith non-holonom ic constraints[C]//Proceedings of IEEE In ternational Con ference on Robotics and Automation.Nice，France:IEEE，1992:1999-2004.

[2] Coelho P，Nunes U.Lie algeb ra application tom obile robot control:a tutorial[M].Camb ridge University Press，2003:483-493.

[3] 吴卫国，陈辉堂，王月娟.移动机器人全局轨迹跟踪控制[J].自动化学报，2001，27(3):326-331.

[4] Kanayama Y，Kimura Y，M iyazaki F.A stable tracking controlmethod for an autonomousmobile robot[C]//Proceedings of IEEE In ternational Conference on Robotics and Autom ation.Piscataway，USA:IEEE，1990:384-389.

[5] 马保离，霍 伟.移动小车的路径跟踪与镇定[J].机器人，1995，17(6):358-362.

[6] Lee S，Park JH.Dynam ic path follow ing using temporary path generator for mobile robots with non-holonom ic constrain ts[C]//Proceedings of IEEE In ternational Conference on Systems，Man and Cybernetics.Tok yo，Japan:IEEE，1999:631-636.

[7] 武 星，楼佩煌，杨 雷.基于视野状态分析的机器人路径跟踪智能预测控制[J].机器人，2009，31(4):357-364.

[8] 肖本贤，刘 刚，余 雷，等.基于MMAS的机器人路径规划[J].合肥工业大学学报:自然科学版，2008，31(1):63-67.