超冗余全方位移动操作臂的逆运动学求解

徐慧娜，闫继宏，于振中，陈志峰，赵 杰

(哈尔滨工业大学机器人研究所，哈尔滨150080，xuhuina511@yahoo.com.cn)

全方位移动操作臂与固定基座的操作臂相比，不但扩大了操作空间，而且大大增强了操作灵活性，提高了适应复杂作业及多任务需求的能力.但是冗余度机器人的逆运动学求解也更加复杂，如何寻找一种能够兼顾优化、速度和精度的算法成为关键.

近年来国内外对于冗余度机器人逆运动学求解方法已经有了一定的研究［1］.传统算法有梯度投影法［2］和最小范数解［3］等.Galicki等［4］研究了考虑控制反馈的逆运动学求解方法.美国CESAR机器人［5］的逆运动学用Jacobian矩阵分块等方法，简化了梯度投影法中求Jacobian矩阵的逆.JIA等［6］基于关节极限及位形优化提出一种简化的逆运动学控制方法.Ma等［7］对操作臂末端自由度进行合理分配，并引入两个约束条件，极大地方便了逆运动学的求解.刘达等［8］针对不存在解析逆运动学解的机器人结构，提出一种解析与数值相结合的求逆解算法.祖迪等［9］在梯度投影法的基础上用固定关节法进行二次计算.叶平等［10］提出了一种冗余度机器人自运动变量选取的新方法.以上方法各有优缺点，但都无法兼顾求逆解的优化性、快速性和精确性.

本文针对所研制的9自由度超冗余全方位移动操作臂，提出了一种快速准确优化的逆运动学求解方法.该方法根据机构特点在位姿分离的基础上，对自由度合理分组，分别基于关节等效和局部优化的原则解除冗余，从而实现快速准确地求解.抓取目标物体的仿真实验证实了该方法的有效性.

1 全方位移动操作臂运动学模型

如图1所示，该移动操作臂由一个全方位移动平台和一个固定在其上的轻型操作臂组成.其中，全方位移动平台在平面内具有3个自由度(x，y，φ);操作臂具有6个自由度θi(i=1，2，…，6).杆件参数及坐标系如图2所示，{OW}和{OB}分别表示世界坐标系和固定在移动平台上的坐标系，{Oi}(i=0，1，…，6)表示操作臂上的D－H坐标系.

图1 全方位移动操作臂实物照片

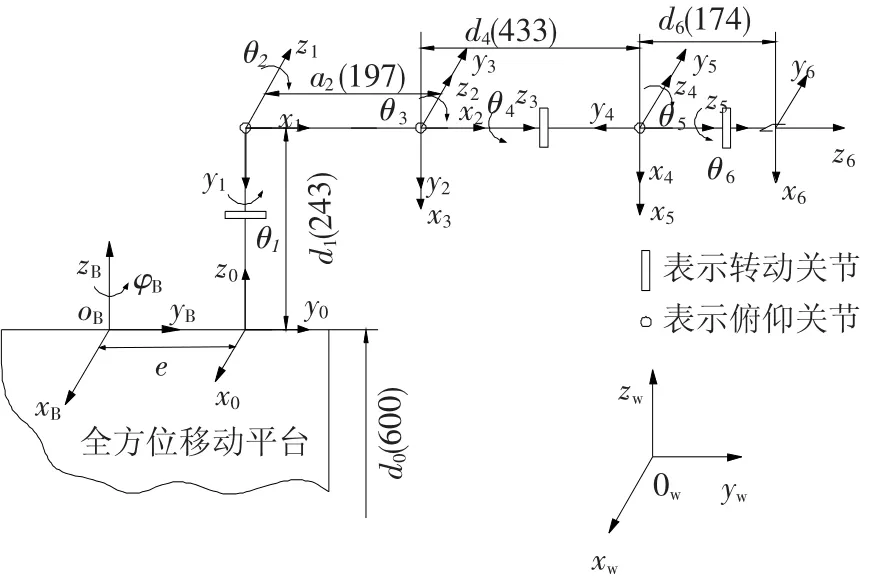
图2 全方位移动操作臂运动坐标系

根据图2可知，全方位移动操作臂的正运动学模型可表示为

其中:

这里，c θi≡cos θi，s θi≡sin θi

2 全方位移动操作臂逆运动学分析

移动操作臂末端3个关节的轴线相交于一点(腕点W)，共同决定末端手爪的姿态;其余6个关节决定腕点的位置.因此，只有在位置逆运动学的求解中才存在冗余自由度.下面将重点论述如何用一种简单、优化的方法来实现位置逆运动学的求解.

由图2及式(1)可知，操作臂末端手爪在世界坐标系{OW}下的位姿矩阵可表示如下:

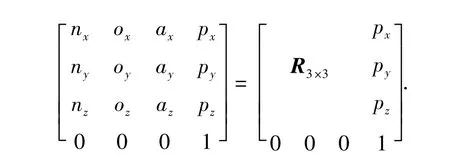
其中，(x，y，φ，θ1，θ2，θ3)决定腕点的位置，(θ4，θ5，θ6)决定手爪的姿态.决定位置的6个变量可以分为两组:

1)腕点W在xWoWyW平面内的投影位置由全方位移动平台的平动自由度x和y，转动自由度φ以及操作臂的第一个回转自由度θ1实现.

2)腕点W沿zW方向的高度由操作臂的第2、第3个转动自由度θ2，θ3来实现.

对于以上两组自由度变量，下文将采取两种不同的方法分别处理.

2.1 关节等效法

全方位移动平台的转动自由度φ与操作臂的第一个回转自由度θ1的旋转轴方向相同，两关节具有等效性.在实际控制时，可以固定其中一个关节不动.臂的初始位置如图2所示，为了保持操作臂始终位于车的正前方，以拥有较大的操作空间，可设定θ1=0.根据目标物体的位置坐标(px，py，pz)，不妨可以预先设定:

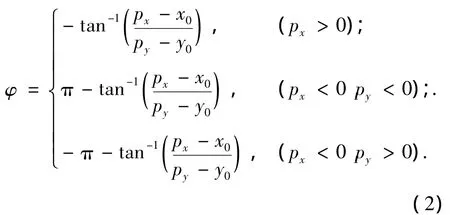
其中(x0，y0，0)为移动平台的当前位置.于是根据关节等效的原理简化了2个自由度，决定位置的自由度数由6个减为4个.

2.2 局部优化法

操作臂的第2，3个转动自由度θ2和θ3的旋转轴方向相同，共同决定腕点W在zW方向的高度.但是，这两个关节在增强操作臂的灵活性方面具有很重要的作用，故采用优化的方法处理.首先根据目标物体的位姿矩阵求出末端手爪达到该位姿时腕点的高度HW，然后建立关于θ2，θ3的优化模型.

2.2.1 求取腕点高度

3个关节旋转轴相交于一点的腕部，相当于一个球铰.在根据目标物体的位姿矩阵求取腕点的高度时，可以先将前面的关节与腕部3个关节相分离，然后再将其与腕部球铰连接上即可，不会影响末端手爪的位姿.具体求解方法如下:

在腕点W上建立基准坐标系{OW＇}，{OW＇}的原点与腕点W重合，各坐标轴与世界坐标系{OW}平行，如图3所示.

图3 腕部坐标系示意图

末端手爪在腕点基准坐标系{OW＇}下的位姿矩阵可表示为

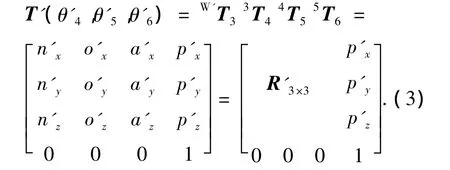
其中:

(为了计算方便，可假设{O3}移至腕点)，4T5，5T6见式(1)，代入式(3)可求得

式中，ci≡cos θi;si≡sin θi.

如前文所述，末端手爪在世界坐标系{OW}下的位姿矩阵为

由于{OW'}与{OW}各坐标轴平行，所以二者的姿态矩阵相等，即R'3×3=R3×3.据此可求出θ'4，θ'5和θ'6，从而求得末端手爪在腕点基准坐标系{OW'}下的位置坐标(p'x，p'y，p'z).

由图3可知，腕点W在zW方向的高度:

需要注意的是，θ'4，θ'5和 θ'6表示坐标系{O3}固定，手爪达到目标姿态时腕部3个关节需要运动的角度.但是实际上{O3}是随着前面几个关节变化的，所以应该在求出θ2和θ3后再代入式(1)求解θ4、θ5和θ6.二者之所以数值不同，只是由于相对的基准坐标系不同，实际腕部3个关节的位姿并没变.所以，由此求出的HW是可靠的.

2.2.2 建立优化模型

根据图2所示，HW只与θ2和θ3两个变量有关，三者满足以下关系式:

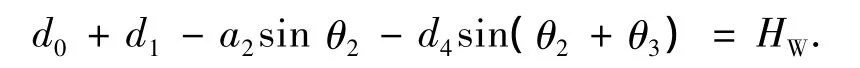
式中，d0，d1，a2，d4为系统结构参数，是已知量.

为了降低系统能耗，并使操作臂在工作过程中保持最好的柔顺性，以关节角运动幅度最小为优化指标.建立的目标函数为

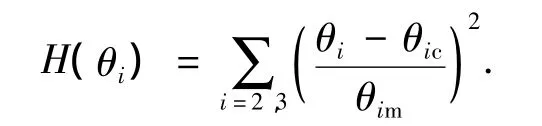
式中:θic为关节i运动范围的中值;θim为关节i运动范围的一半.在该全方位移动操作臂系统中，θ2和θ3的运动范围均为(－π/2，π/2).这样，操作臂第2，3个关节θ2和θ3的优化求解便转化为有两个未知数和一个约束条件的二元函数的条件极值问题.相比Dubby对CESEAR七自由度机器人逆运动学提出的梯度投影算法(计算量为141个乘法，102个加法)，显然大大减小了计算量，保证了实时性的要求.

经过等效关节和局部优化求解之后，该系统的9个自由度便只剩下5个自由度是未知的.具体求解过程同普通的非冗余机器人逆解求解方法，在此不再赘述.以上所求的逆解均为精确的解析解，满足了准确性的要求.

3 仿真实验

设目标矩阵为

假设初始时刻移动平台位于世界坐标系原点，抓取过程中无障碍，采用点到点(PTP，pointto-point)的轨迹规划方法，时间为5 s.注意到:如果是固定基座的操作臂，末端手爪无法到达目标点.所以全方位移动平台极大地扩展了操作臂的工作空间.

目标点的位置坐标(5 000，5 000，1 000)，由式(2)可得φ=－π/4.根据上述逆运动学求解方法求得其他各个关节变量，采用基于关节变量描述的插值算法得到各关节的MATLAB仿真曲线如图4所示.

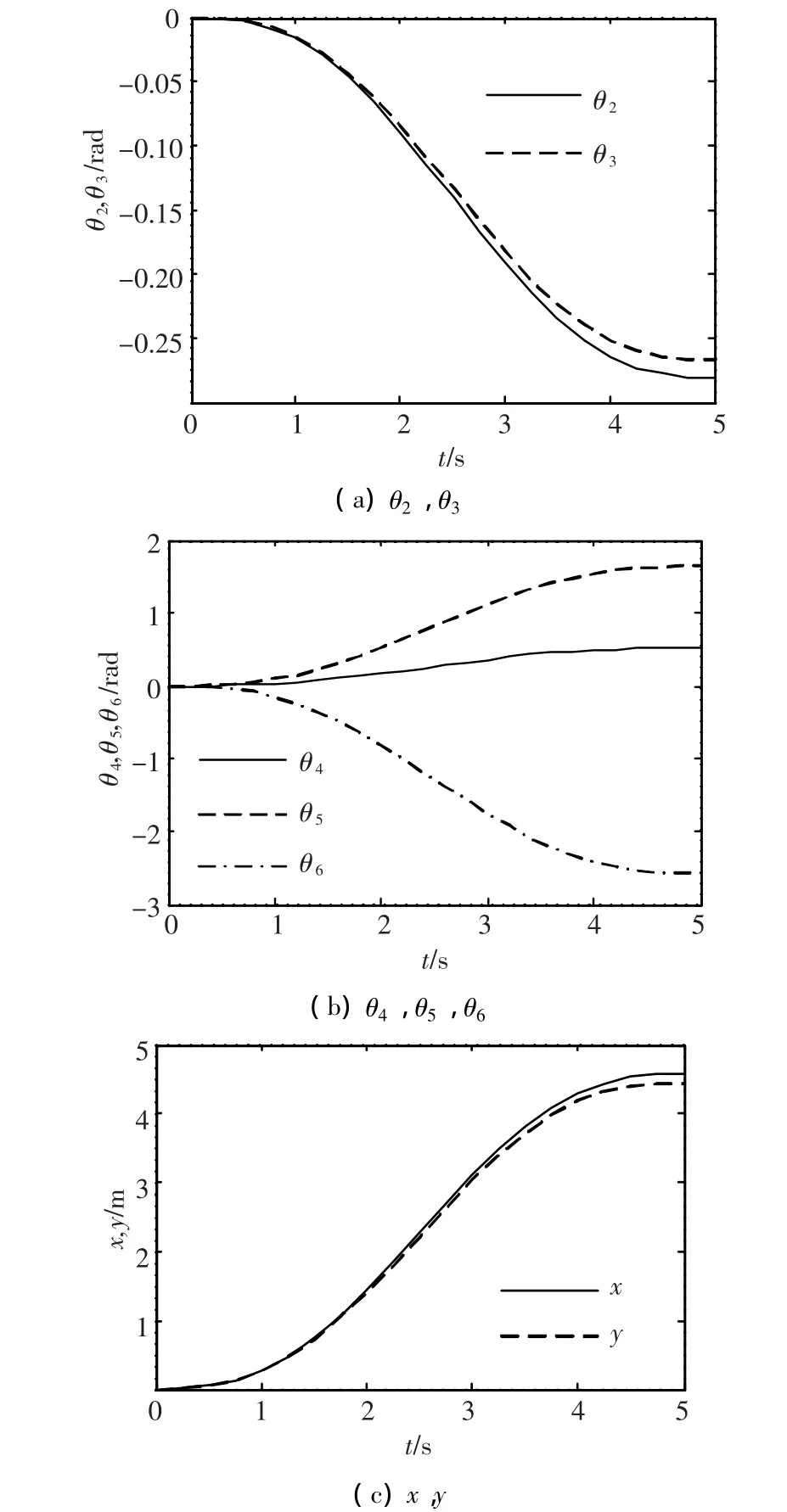
图4 各关节的位移曲线

其中，θ2，θ3，θ5的运动范围为(－π/2，π/2)，θ4，θ6的运动范围为(－π，π)，由图4可知各关节均未超出其运动范围，且曲线连续平滑，可以实现平稳抓取.

末端手爪轨迹的三维视图及分别在xW，yW，zW方向的视图如图5所示.

由图5可以看出利用该逆解算法可以实现末端手爪对目标点的准确抓取.

在运算时间方面，在Pentium(R)4 2.4GHz处理器上采用Windows XP操作系统对该逆运动学求解方法进行了时间测试.通过多次计算求均值的方法估算每次求解耗时6 ms左右，控制周期约为20 ms，完全可以满足一般机器人系统的实时性要求.

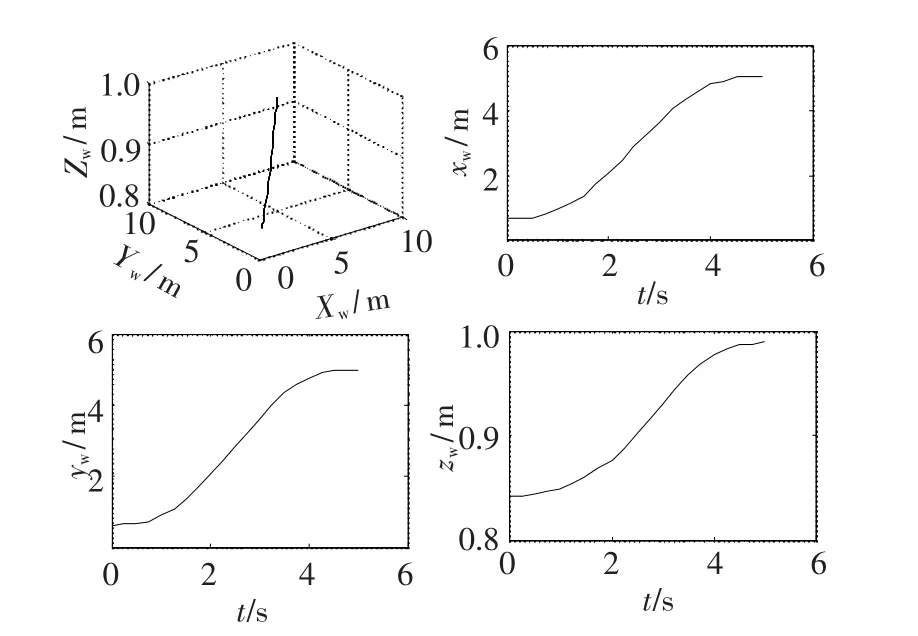
图5 末端手爪的位移曲线

4 结论

1)针对一类9自由度超冗余全方位移动操作臂，在位姿分离的基础上，分别利用关节等效和局部优化的方法处理不同的冗余自由度.

2)提出了一种根据手爪姿态求取腕点位置的方法，从而把关于两个变量的优化问题转化为二元函数的条件极值问题，提高了优化计算的速度.

3)仿真实验证明该方法能够在兼顾优化的前提下快速地求取解析逆解，对冗余度移动操作臂的逆运动学求解具有一定的通用性.

［1］刘迎春，余跃庆，姜春福.冗余度机器人研究动向［J］.机械设计与研究，2003，19(1):23－27.

［2］LIEGEOIS A.Automatic supervisory control of the configuration and behavior of multibody mechanisms［J］.IEEE Trans，System，Man，Cybemetics，1977，7(12): 868－871.

［3］CHAN T F，DUBEY R V.A weighted least-norm solution based scheme for avoiding joint limits for redundant manipulator［C］//Proceedings of IEEE International Conference on Robotics and Automation.Atlanta，USA:［s n.］，1993:395－402.

［4］GALICKI M.Control-based solution to inverse kinematics for mobile manipulators using penalty functions［J］.Journal of Intelligent and Robotic Systems，2005，42 (3):213－238.

［5］DUBEY R V.Real-time implementation of an optimization scheme for seven-degree-of-freedom redundant manipulators［J］.IEEE Tr on Robotics and Automation，1991，7(5):579－588.

［6］JIA Qing-xuan，ZHAN Qiang，SUN Han-xu，et al.Implementation and kinematic control of a hyper-redundant mobile manipulator System［J］.Chines He Journal of Aeronautics，2006，19(1):83－88.

［7］MA Bojun，FANG Yongchun，ZHANG Xuebo.Inverse kinematics analysis for a mobile manipulator with redundant DOFs［C］//Proceedings of the 26th Chinese Control Conference.Zhangjiajie，China:［s n.］，2007:118－122.

［8］刘 达，王田苗.一种解析与数值相结合的机器人逆解算法［J］.北京航空航天大学学报，2007，33(6): 727－730.

［9］祖 迪，吴镇炜，谈大龙.一种冗余机器人逆运动学求解的有效方法［J］.机械工程学报，2005，41(6):71－75.

［10］叶 平，孙汉旭，张秋豪.基于自运动控制的冗余机器人运动学优化［J］.机械工程学报，2004，40(12): 128－132.