一种估计舰空导弹脱靶量的方法

裴 喆，史 震

（1.哈尔滨工程大学 自动化学院，哈尔滨 150001；2.92941 部队，辽宁 葫芦岛 125001）

在靶场进行舰空导弹拦截靶标（靶机或靶弹）飞行试验时，脱靶量是必须测量的参数，因为它是衡量导弹在弹道末端制导与控制性能的关键指标。脱靶量测量一般采用两种方法：一种是设法测量导弹和靶标的外弹道数据，利用遭遇段的空间位置参数重建弹靶运动轨迹，外推计算脱靶量[1]。目前主要采用地面雷达或光电经纬仪进行外弹道测量，雷达测量精度较低，光电经纬仪测量精度高但易受气象条件影响。另一种则是设法测量遭遇段弹靶之间的多普勒频率，根据脱靶量与多普勒频率之间的数学关系估计脱靶量[2-3]。目前主要采用遥测或靶机专用脱靶量测量设备进行多普勒频率测量，靶机专用脱靶量测量设备精度较高，但重复测量成本高，且无法装在靶弹上。遥测是靶场主要的内弹道测量方法，技术成熟、工作可靠，遥测数据中包含引信探测的多普勒频率。实际弹靶遭遇时，由于靶标体目标效应的影响，多普勒频率经常包含许多孤立野值和成片野值，而如何去除成片野值在公开发表的文献中还没有见到通用有效的方法[4]。本文首先讨论利用无野值的多普勒频率估计脱靶量的方法，然后研究利用小波分解识别并去除野值的方法。

1 脱靶量数学模型

导弹和靶标遭遇过程中，由于相对速度大，遭遇时间短，可以认为相对速度保持不变。脱靶量数学模型如图1所示，图中rV为导弹相对靶标的运动速度，ρ为脱靶量（ρ垂直于 Vr），ti为多普勒频率采样时间，tρ为脱靶时间。

图1 脱靶量数学模型

对于不同的ti(i=1,2,3,…,n)，多普勒频率Ed(i)与脱靶量ρ的数学关系可由式(1)表示[2]：

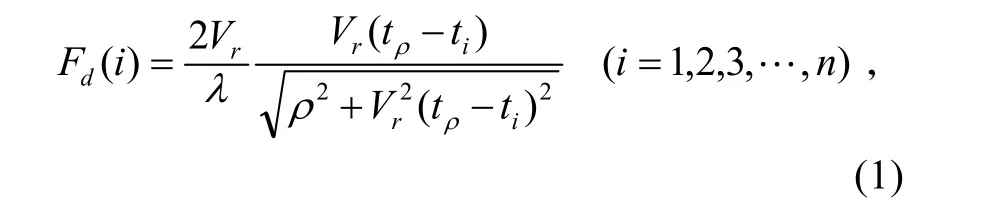
式中：λ为引信天线波长；Vr可由引信开机前的导引头遥测数据得出。由于引战配合需要，引信在 tρ到来前引爆战斗部，tρ时没有Ed(i)数据，tρ和ρ只能由已测的Ed(i)数据根据式(1)计算得到。实际遥测测量的多普勒频率fd(i)可由式(2)表示：

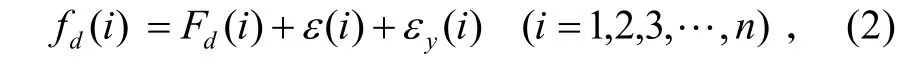
式中：ε (i)表示随机误差；εy(i)表示野值。

利用fd(i)估计ρ 需要尽量消除 ε (i)和 εy(i)，从而得到与Ed(i)非常接近的曲线。

2 多普勒频率数据仅含随机误差时的脱靶量估计

先讨论fd(i)仅含随机误差ε (i)的情况，即εy(i)=0。多数情况下 ε (i)近似于零均值高斯白噪声，一般采用拟合或滤波的方法去除 ε (i)。小波变换可同时进行时域和频域分析，具有可变的时频分辨率，通过小波多尺度分解可将信号分解为反映整体趋势的低频分量和反映噪声细节的高频分量。

对fd(i)利用db4 小波进行4层分解，得到低频系数a1、a2、a3、a4和高频系数d1、d2、d3、d4，再对各层系数进行重构。分析各层系数发现：从第1层到第4层，高频系数将噪声按频率降低的顺序分别提取出来；低频系数所含噪声越来越少，多普勒频率趋势越来越明显。a1与fd(i)曲线如图2所示，由于d1提取了白噪声最尖锐的部分，a1不但没有丢失Ed(i)的有用信息，而且比fd(i)光滑许多。对a1进行最小二乘拟合，使其与拟合曲线fd' (i)残差序列的平方和 S (i)最小，表达式如式(3)所示：

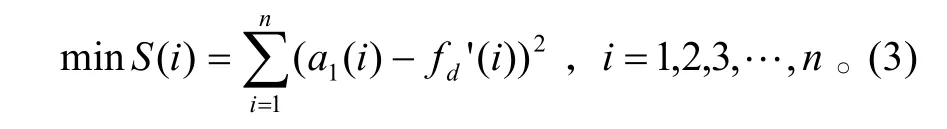
最后由fd' (i)根据式(1)计算出ρ。

图2 无野值多普勒频率a1系数的拟和结果

为验证方法的可行性和有效性，现利用蒙特卡洛方法进行仿真。给定 Vr、tρ、ρ、ti的一组设定值，取 Vr=1 200 m/s、tρ=30.000 s、ρ=10 m、ti=29.992 s时引信起爆。由式(1)得到Fd(i)，再模拟生成 ε (i)～N(0，1 0002)，按式(2)合成fd(i)序列。然后对fd(i)序列的小波系数a1进行最小二乘拟合，得到ρ和 tρ的估计值。由于Fd(i)都是ρ和 tρ的非线性函数，须采用非线性最小二乘拟合[5]。仿真1 000次的统计结果如表1所示，可以看出：

a）利用a1进行拟合精度很高，其中一次的拟合曲线fd' (i)如图2所示，fd' (i)与Fd(i)几乎重合。ρ的估计均值与设定值仅差约0.01 m，估计标准差仅约为0.24 m。统计还表明ρ的估计值近似服从正态分布，因此ρ的估计精度能够控制在（−0.75 m～+0.75 m）范围内，完全满足测量要求。

b）由于对实际数据进行拟合时事先并不知道真值，仿真中设定了3组不同的初值，结果表明拟合算法对不同初值有很好的收敛性。

因此，当多普勒频率数据仅含随机误差时，利用该拟合算法估计脱靶量是可行而且有效的。

表1 a1系数拟合统计结果

3 多普勒频率数据有野值时的脱靶量估计

3.1 野值识别

式(2)中的εy(i)表示野值，一批数据中有部分数据与其余数据相比明显不一致的称为野值，或称离群值、异常值[6]，一般分为孤立型和成片型。由于弹靶遭遇时靶标的体目标效应影响，实际的引信多普勒频率数据经常含有野值。直接对有野值fd(i)的a1系数进行拟合，结果的局部图如图3所示。拟合曲线fd' (i)与Fd(i)偏离较大，ρ估计值也与设定值有较大偏差，因此必须对野值进行识别、去除。

图3 有野值多普勒频率a1系数的拟和结果

通过随机加入不同类型、不同数量、不同位置、不同幅值的野值 εy(i)对fd(i)进行模拟，利用db4小波进行4层分解，将重构后的各层系数与无野值多普勒频率小波分解后的各层系数对比分析发现：

a）孤立野值和白噪声主要影响d1的幅值，因此a1能反映成片野值的轮廓，定位比较准确，a1局部图如图3所示。而且a1与拟合曲线fd' (i)的残差序列能够反映成片野值的大小。

b）成片野值主要影响d2、d3，它们局部幅值的增大说明成片野值的存在。如果设置一定门限可用于成片野值的识别，且这种识别方法与拟合曲线fd' (i)无关。

由此可总结出fd(i)有无野值的识别准则：

a）孤立野值和两点成片野值可直接利用fd(i)与拟合曲线fd' (i)的残差序列识别，门限值一般取

±3σ。[7]

b）成片野值可利用d2、d3的局部幅值识别，门限值可通过与无野值多普勒频率的d2、d3幅值统计比较得到。

c）成片野值也可利用a1与拟合曲线fd' (i)的残差序列识别，多次仿真发现无野值多普勒频率的a1与拟和曲线fd' (i)的残差序列中几乎没有连续三点数据幅值都超过1.5σ的。因此，识别两点以上成片野值的门限值可取±1.5σ。

3.2 野值去除

3.2.1 野值去除顺序

确定野值去除顺序应首先分析野值的特殊性，通过对不同类型、数量、位置、幅值的野值进行模拟发现：若幅值相同、分布位置相同，则成片野值相比孤立野值对拟合影响大；若幅值相同、类型相同，则位于后半区的野值比前半区的对拟合影响大，这是因为多普勒频率是非线性的，离靶标较远时变化较缓，较近时急剧下降。另外，由于靶标体目标效应逐渐增强，通常后半区野值数量更多，幅值更大，且起伏剧烈。由于这些特性，拟合曲线fd' (i)对Fd(i)有时有较大偏离（尤其后半区），如图3所示。

野值有正有负、有大有小，导致fd' (i)对Fd(i)有不同的偏离方向和不同的偏离程度，因此野值去除顺序必须保证fd' (i)向Fd(i)逐步收敛。偏离的方向有全区上升、全区下降、前降后升、前升后降4种情况。全区上升时必须先去除正野值，后去除负野值；全区下降时与之相反。由野值的特殊性决定，前降后升时必须先去除后半区正野值和前半区负野值，最后去除其他野值；前升后降时与之相反。为表征fd' (i)偏离Fd(i)的方向和程度，将a1与fd' (i)的残差序列定义为偏离因子，因为该序列能够较准确地反映成片野值的位置和幅值。偏离因子初始值为0，它的正负对应野值的正负，它的大小对应偏离的程度。将偏离因子大小根据成片野值不同的长度、幅值、位置进行分档，长度越长、幅值越大，则偏离因子越大，且后半区的偏离因子比前半区的大。再将残差序列按时间等分为几个（一般6个即可）分区，计算各分区偏离因子以及全区偏离因子总和，这样就可以识别偏离方向及程度了。全区上升或下降表现为全区偏离因子总和较大，且各分区偏离因子大部分为正或大部分为负。前降后升或前升后降表现为全区偏离因子总和较小，且前半区的偏离因子与后半区的偏离因子正负相反。

由此可总结出野值去除的顺序：先确定拟合曲线的偏离方向和程度；然后对比前后半区，若后半区野值多则先去除，少则全区同时去除；无论哪个区域都须先去除较长成片野值，再去除较短成片野值，最后去除孤立野值。

3.2.2 野值替换方法

野值替换是指在野值点fd(j)处的拟合曲线fd' (j)数据增加适当的调整值（一般为k⋅σ），生成新的fd(j)数据：

孤立野值替换直接使用式(4)。成片野值替换需调整为式(5)：

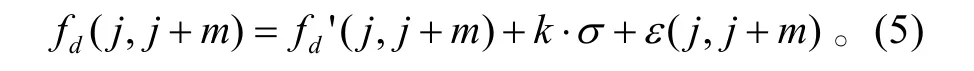
因为如果成片野值的替换数据相同会影响再次拟和的结果，所以应在式(4)基础上增加与成片野值相同长度的零均值高斯白噪声ε (j,j+m)～N(0,σ2)，m+1为成片野值长度。

k的正负与野值的正负相反，野值为正时，调整值为负；野值为负时，调整值为正。k的大小取决于拟和曲线fd' (i)偏离Fd(i)的程度，可用仿真统计的方法确定k的取值范围。

3.3 算法仿真

为验证野值识别和去除方法的有效性，并确定k的取值范围，编制了仿真程序，程序流程分为：

第1步：模拟生成如式(2)所示的fd(i)数据。其中野值 εy(i)由人工随机设置，成片野值长度最长为7点，幅值最大5倍σ，数量不大于全部数据的二分之一。

第2步：利用db4 小波对fd(i)进行4层分解，并重构各层系数。对a1进行非线性最小二乘拟合，得到拟合曲线fd' (i)、拟合残差序列及ρ的估计值。

第3步：按3.1节中的准则对fd(i)进行野值识别，若有野值，执行第4步；若无野值，则程序结束，ρ即为所求脱靶量。

第4步：按3.2节中的方法去除部分野值，对野值替换后生成的新fd(i)数据循环执行第2步。

通过设置不同野值进行仿真后结果表明，k的取值范围主要与野值分布有关。后半区野值较少时，全区替换时k 一般在0＜k≤1范围内取值；后半区野值较多时，后半区k的取值范围能达到 0＜k＜2，将后半区大部分野值替换后，再在0＜k≤1范围内取值对全区替换即可。

为提高替换精度，可将 k⋅σ的大小按0.25·σ分档，即0.25·σ、0.5·σ、0.75·σ、σ，具体选档需根据拟合曲线偏离程度确定。

仿真还表明，如果野值数量小于全部数据的三分之一，后半区野值较少时，野值去除后的脱靶量估计精度能控制在（−1 m～+1 m）范围内；后半区野值较多时，也能控制在（−1.5 m～+1.5 m）范围内，仍能满足测量要求，表明算法是合理有效的。但如果野值数量大于全部数据的三分之一，拟合曲线有时会发散。

4 结束语

本文研究了一种利用小波分解和非线性最小二乘拟和相结合估计舰空导弹脱靶量的方法。通过仿真验证可知，对于同时含有成片野值和孤立野值的引信多普勒频率数据，如果野值数量小于全部数据的三分之一，则利用该方法估计的脱靶量误差在（−1.5 m～+1.5 m）范围内，满足测量要求，但野值较多时的去除方法仍需加以研究。

[1]袁俊.由雷达测量数据求解脱靶量算法研究[D].南京:南京理工大学,2003.

[2]林松.用导弹“视频遥测”信号推算导弹脱靶量[J].上海航天,2002(3):35-38.

[3]魏国华,吴嗣亮,王菊,等.脱靶量测量技术综述[J].系统工程与电子技术,2004,26(6):768-772.

[4]胡绍林,孙国基.靶场外测数据野值点的统计诊断技术[J].宇航学报,1999,20(2):68-74.

[5]张光澄.非线性最优化计算方法[M].北京:高等教育出版社,2005:159-168.

[6]张德然.统计数据中异常值的检验方法[J].统计研究,2003(5):53-55.

[7]费业泰.误差理论与数据处理[M].5 版.北京:机械工业出版社,2008:43-49.