带附加供料的准理想级联模型及其在回收铀浓缩中的应用

谢全新 丛艺坤 吴建军

(核工业理化工程研究院 天津 300180)

同位素分离级联的理论研究和设计通常以某种模型级联为基础。二元分离情况下的模型级联叫理想级联[1]，即在级汇合点无丰度混合损耗的级联。在多组分同位素分离理论中，模型级联称准理想级联[2–7]，实际上不能实现，但其中的一些基本物理规律可为实际级联的改善和优化提供重要参考。另外，与实际级联计算相比，模型级联计算有解析求解、算法简单的特点。

某些特殊的分离任务需借助附加供料级联，如核燃料循环中回收铀的再浓缩[8]及某些分离过程对轻杂质的净化[9]。本文建立带附加供料的准理想级联的数学模型，并分析研究回收铀再浓缩级联的有关特性。

1 多组分级联基本参量和准理想级联

级联是由多个分离级按一定方式联接而成，每个分离级由一定数量分离器并联。流量为L的供料流入分离级，其同位素组分丰度为Ci(i=1……m，m为同位素混合物的组分数)。从分离级流出流量 L′的浓缩流(或轻馏分)和流量L"的贫化流(或重馏分)，相应的组分丰度为和。

定义θ=L′/L为级分流比，这样L′、L"通过供料流L表达：

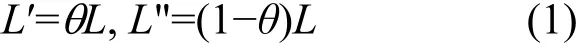
定义φi=Li′/Li为级的组分分流比：

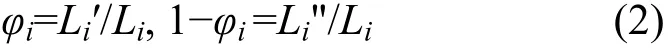
其中，Li=LCi, Li′=L′Ci′, L"i=L"Ci"。

若分离过程中并无物质损耗，则分离级三股流及相应的组分流满足如下物质守恒方程：

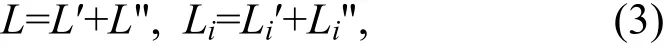
且

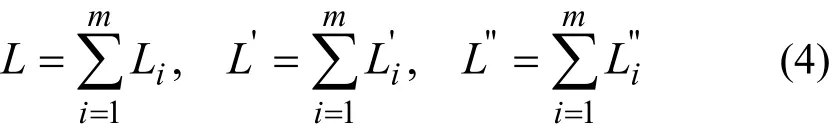
如把第k组分作“关键”组分， 则i、k两组分在供料流、浓缩流和贫化流中的相对丰度 Rik、Rik′和Rik"，以及全分离系数 qik、浓化分离系数αik和贫化分离系数βik，可表示为：

通常相对全分离系数随级的供料丰度 Ci和分流比θ变化而变化，但对大部分基于分子动力学的分离方法，相对全分离系数基本不随上述参量改变，表示为：

其中，q0为基本全分离系数，Mk、Mi表示第 k、i两组分的摩尔质量。

为理论描述方便，引入参量

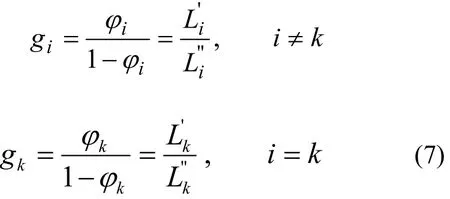
由式(1–2)、(5)及(7)，可有：

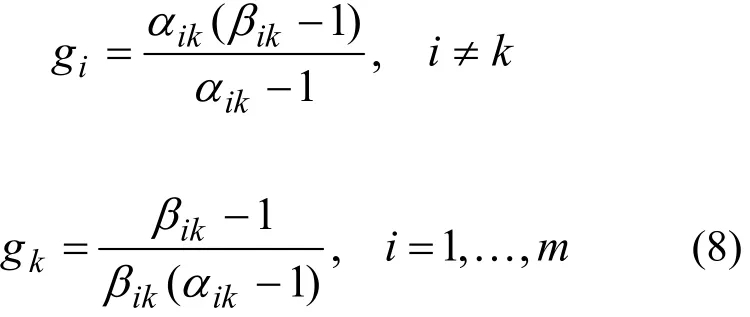
多组分同位素分离级联中，如果组分分流比ϕi在级联各级中保持不变，则为准理想级联。组分分流比各级恒等的条件是各级的 qik、αik和βik保持不变。

用式(2–7)得到级联第s级的L(s)、Ci(s)及θ(s)：

另一重要概念是丰度比匹配级联(Matched abundance ratio cascade，简称M级联)，是准理想级联的一种特殊情形，满足在级汇合点处选定的两组分(如第n、k组分)的相对丰度相等，即：

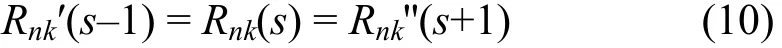
这种情况下，gi可用q0及组分质量数表达：

其中

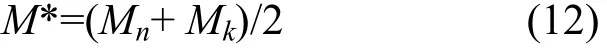
2 带附加供料的准理想级联的数学模型

带附加供料的准理想级联的外参量有主供料流F、贫料流W、精料流P及附加供料流E，各股流中相应组分丰度分别为CiF、CiW、CiP和CiE。级联总级数N，精料和贫料分别从第N级和第1级取料。此外，主供料流从第 f级供入，附加供料流从第 l级供入。

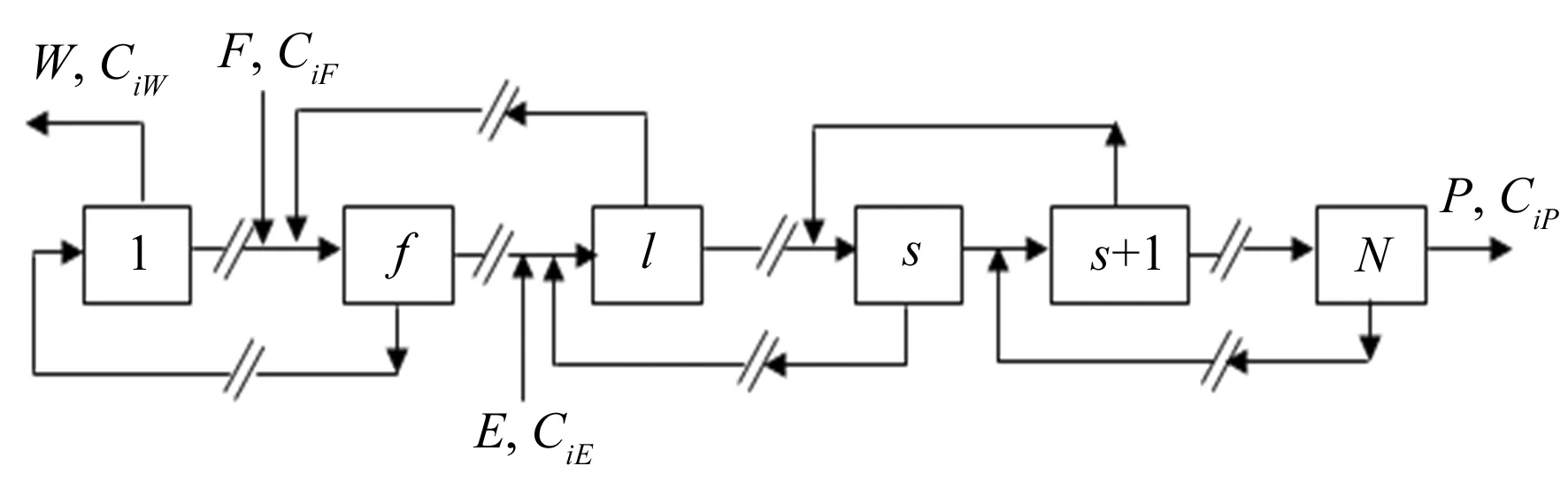
图1 带附加供料的准理想级联示意图Fig.1 Scheme of a quasi-ideal cascade with an additional feed flow.

假设级联稳态运行，且无腐蚀损耗，对任意 s级(s≠f，s≠l)，如下组分质量守恒方程成立：

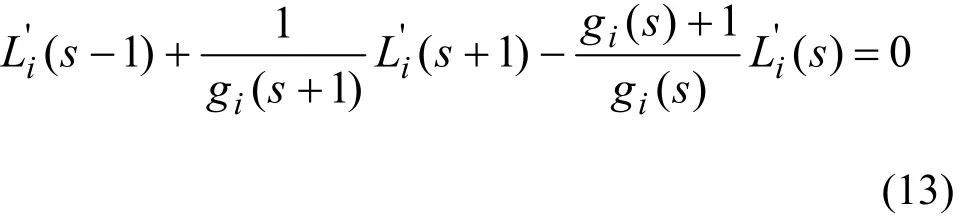
准理想级联中，分离系数αik、βik、qik、ϕi及gi各级相等。这种情况下，方程(13)属于二阶线性差分方程，其解可表示为：

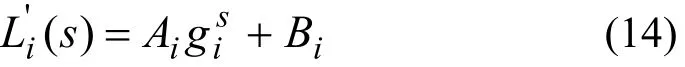
其中，Ai、Bi为常数，值由具体边界条件确定。在级联精料端、贫料端、主供料级和附加供料级的边界条件为：

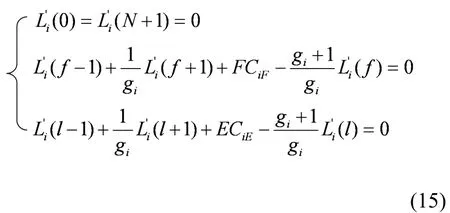
级联组分守恒方程为：

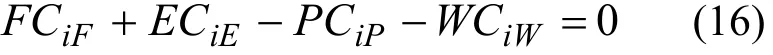
用式(15、16)求得级联方程(13)在级联各段的解：

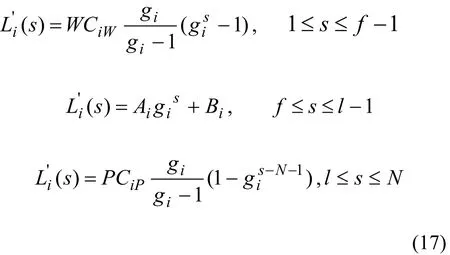
其中

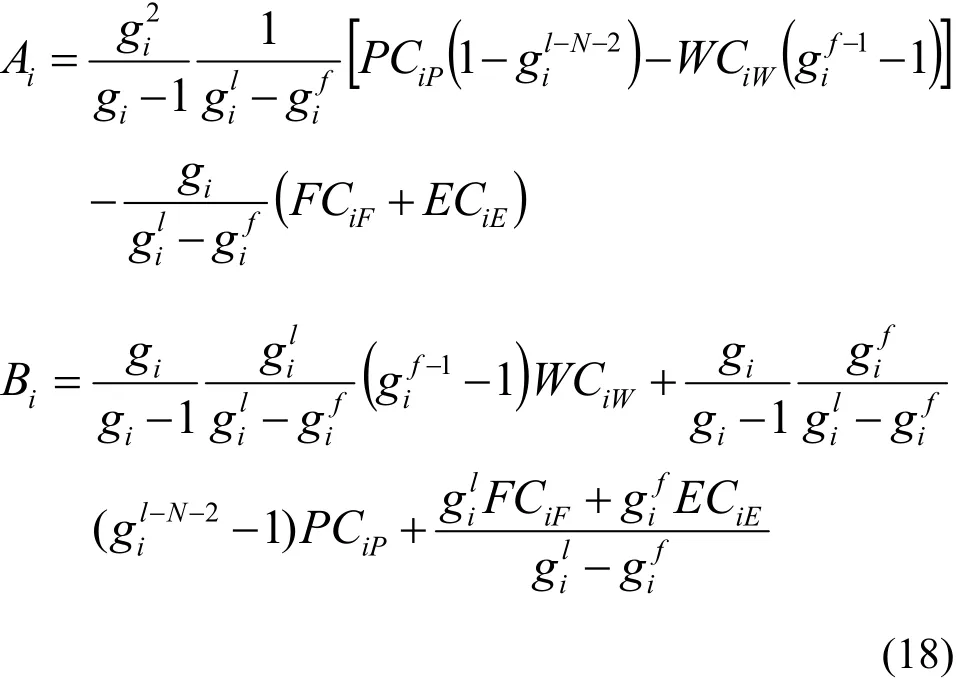
把式(17)代入第f–1级组分守恒方程：

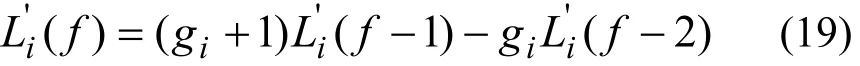
并考虑到式(16)，可得到：

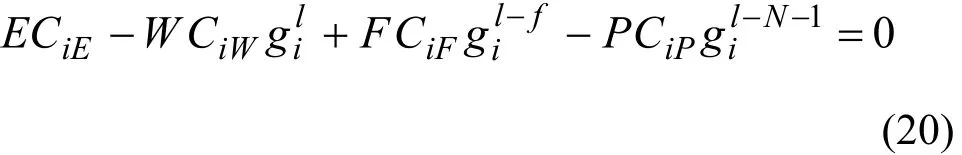
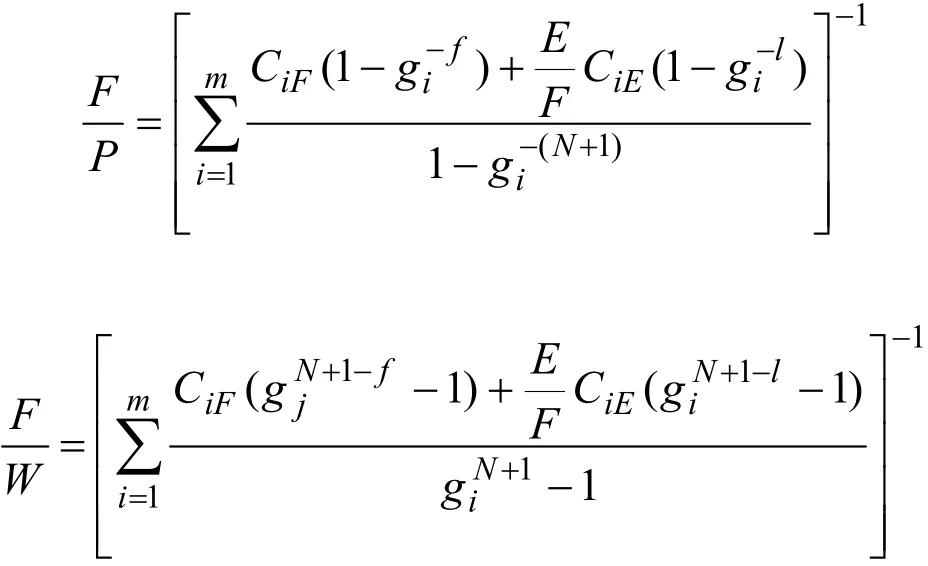
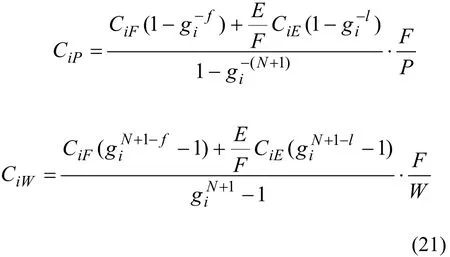
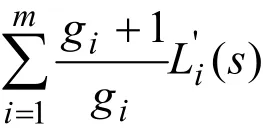
如给定参量CiF、CiE、gi、N、f、l和E/F，由式(17、18)确定级联各级轻馏分中第i组分的Li'(s)，由式(21)求解级联的CiP和CiW，由(22)求出级联中总的物质流量，根据式(9)求级联的L(s)、Ci(s)及θ(s)。

3 带附加供料流的准理想级联在回收铀浓缩中的应用

乏燃料后处理是实现核燃料循环、保证核电持续健康发展的重要环节。后处理可从乏燃料中回收铀，提高铀资源的利用率。反应堆使用浓缩铀(235U丰度 3%–5%)，从乏燃料中回收铀必须送到浓缩工厂，浓缩到所需丰度才能再利用。相对分离天然铀，回收铀的分离较复杂，因为[8]：

(1) 铀核燃料在燃烧过程中，部分235U经(n,2n)反应生成234U，进一步经(n,3n)反应生成232U，而232U及其衰变产物有γ辐射[10–12]。回收铀前须除去232U或将其稀释到允许丰度值。浓缩后回收铀的232U与235U丰度比一般须满足[13]：

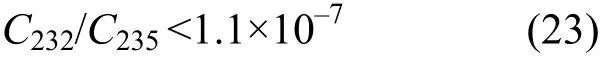
(2) 回收铀的浓缩问题属于多组分同位素分离问题。根据级联分离理论，当235U在级联精料端浓缩时，232U也浓缩且浓缩程度高于235U。若用普通级联浓缩回收铀，级联精料端的C232/C235将变大，不能实现232U稀释。同时，236U与235U摩尔质量很接近，与238U相对分离系数相差无几，所以236U也将在精料端浓缩，不利于回收铀的再利用。

用带附加供料的准理想级联能解决上述问题。天然铀作主供料，回收铀作附加供料。选择UF6作分离工质。含天然铀和回收铀的UF6化合物中各组分的摩尔质量及丰度列于表1。

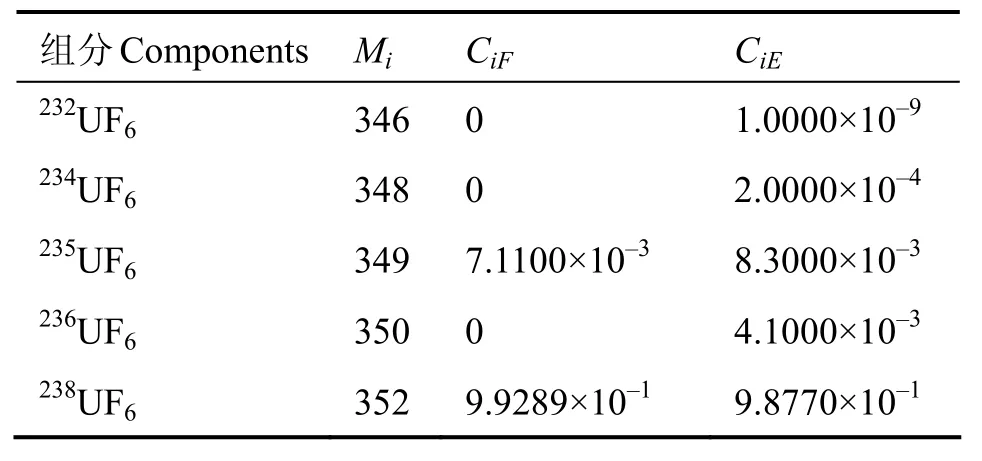
表1 天然铀和回收铀中各组分的摩尔质量及丰度Table 1 Component molar masses and abundances in the native and recycled uranium.

数值计算中，假定235U在级联精料和贫料中丰度分别为C3P=3.5%和C3W=0.2%。232U和235U两组分在精料中丰度满足约束条件(23)。把235U和238U作为关键组分，即式(12)中n=3，k=5。

计算表明，附加供料流量与主供料流量与之比E/F如图2(a)时能满足丰度约束条件(23)。由图2(a)，当235U浓缩到3.5%，贫料丰度为0.2%时，随E/F增加232U和235U丰度之比 C1P/C3P逐渐升高。当E/F=2.37时，C1P/C3P=1.1×10–7，已达约束条件(23)上限。所以E/F不能高于2.37。E/F值上限与回收铀组成尤其是232U和235U两组分的含量密切相关。

多组分同位素分离级联中，级联总的物质流量是重要参量，它的大小对应完成一定分离任务的级联规模，即分离器数目。满足约束条件(23)情况下，级联总的相对物质流量 SL0=LT/P随 E/F变化趋势如图2(b)。SL0随E/F增加而下降，因为回收铀中235U丰度高于天然铀中235U丰度，E/F越大，整个级联的供料丰度增加，由于精料丰度和贫料丰度不变(分别3.5%和0.2%)，这样完成分离任务所需分离功就越小，因而SL0降低。

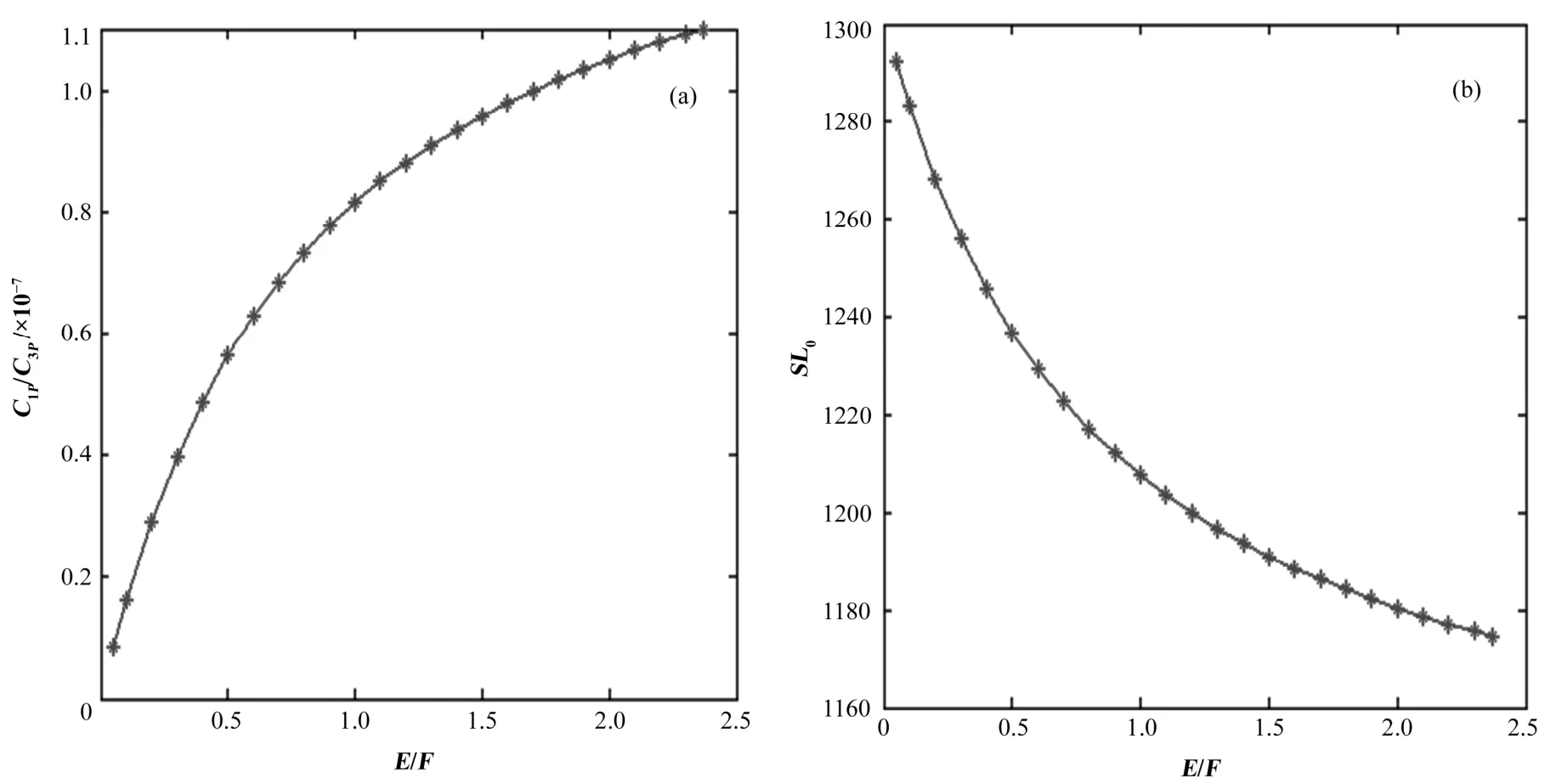
图2 C1P/C3P (a)和SL0 (b)与E/F的关系Fig.2 C1P/C3P (a) and SL0 (b) as a function of E/F.

4 结论

建立带附加供料流的准理想级联的数学模型，得到求解带附加供料的准理想级联中的精料组分丰度、贫料组分丰度及级联中总的物质流量的解析表达式。用带附加流的准理想级联模型对回收铀分离进行级联计算。天然铀作主供料，回收铀作附加供料。把235U浓缩到所需丰度、并满足232U丰度约束条件时，回收铀与天然铀的供料量之比存在一个极限值。

1 Cohen K. The theory of isotope separation as applied to the large scale production of235U. New York: Mc, Graw-hill Book Co Ink, 1951

2 Sulaberidze G A, Xie Q X, Borisevich V D. Ars Separatoria Acta, 2006, 4: 67–77

3 Sulaberidze G A, Borisevich V D, Xie Q X. Theor Foun Chem Eng, 2006, 40(1): 7–16

4 Xie Q X, Sulaberidze G A, Borisevich V D. Proceedings of the XX International Symposium on Physoco-Chemical Methods of the Mixtures Separation,“Ars Separatoria 2005”, Poland , Szklarska Poreba, June 20–23, 2005. 205–207

5 Xie Q X, Sulaberidze G A, Borisevich V D. Proceedings of XI All-Russia (International) Scientific Conference, Physical and Chemical Processes on Selection of Atoms and Molecules. Russia, December 11–15, 2006. 15–20

6 谢全新, 李大勇, 李文泊, 等. 核科学与工程, 2008, 28(1): 86–91

XIE Quanxin, LI Dayong, LI Wenbo, et al. Nucl Sci Eng, 2008, 28(1): 86–91

7 谢全新, Sulaberidze G A, 吴建军, 等. 原子能科学技术, 2009, 43(8): 750–755

XIE Quanxin, Sulaberidze G A, WU Jianjun, et al. At Energy Sci Technol, 2009, 43(8): 750–755

8 谢全新, 李大勇, 吴建军. 核技术, 2009, 32(1): 61–65

XIE Quanxin, LI Dayong, WU Jianjun. Nucl Tech, 2009, 32(1): 61–65

9 贾兴国, 应纯同, 曾 实. 清华大学学报(自然科学版), 2006, 46(3): 371–373

JIA Xingguo, YING Chuntong, ZENG Shi. J Tsinghua Univ (Sci & Tech), 2006, 46(3): 371–373

10 Sinev N M. Economics of nuclear power engineering. Moscow: Energoatomizdat, 1987

11 Zaritskaya T S, Zaritskii S M, Kruglov A K, et al. At Energy, 1980, 48(2): 67–70

12 Buttler G G, Wilcox P. Nucl Eng, 1986, 28(6): 186–190

13 Matveev L V, Tsentner E M. At Energy, 1980, 48(4): 10–17