聚合物熔体流场应力分布的流动双折射测量新方法*

范吉昌 彭响方

(华南理工大学聚合物新型成型装备国家工程研究中心,广东广州 510640)

聚合物加工成型过程中,熔体的流变特性对成型工艺条件的确定及最终制品的结构性能影响显著[1].挤出成型过程中,聚合物熔体的挤出胀大现象与其“弹性记忆效应”[2-3]及其在流动中的拉伸黏度特性[4-5]密切相关.因而,掌握聚合物熔体的流变响应特性,对优化聚合物成型工艺及提高制品的结构性能至关重要.

研究聚合物的流变特性主要有数值模拟和实验测量两类方法.本构方程的选择是影响数值模拟方法准确性的关键,而本构方程中的流变参数需借助各种流变仪由实验数据确定.因此,实验测量聚合物熔体的流变特性是研究聚合物熔体流动本质的必不可少的手段.实验测量方法一般是通过各种流变仪定量描述聚合物熔体应力与应变之间的关系,但这并不能如实描述实际生产加工条件下,聚合物的流变特性.

应用流动双折射技术可以在线测量聚合物熔体在流场中的应力分布.在一定条件下聚合物熔体满足应力 -光学定律[6],这就是应用流动双折射技术测量聚合物熔体在流动中应力分布的理论基础.

传统的双折射测量实验装置一般包括平行激光光源、一对偏振镜和一对 1/4波片.然而,应用这套传统实验装置得到的图像信息中,并不包含计算应力分布所需的取向角(缺少等倾线)[7],所以该图像信息还不足以定量计算流场的应力分布.该方法过去主要用来定量测量对称流道流场中对称轴上的应力分布[8-10],因为对称轴上的取向角被取作 0°.文献[11]分别采用圆偏振光场和平面偏振光场得到等差线和等倾线条纹图,从而计算了流场的应力分布.该方法不能同时测量流场的等差线与等倾线,因而流场的不稳定因素会导致大的测量误差,操作也不方便.

针对上述不足,文中在传统实验装置基础上进行适当的变化,提出一种新的光路系统及测量方法,以同时测量流场的等差线与等倾线,使得测量得到的图像信息不仅包含双折射值,而且包含定量描述流场应力分布不可缺少的取向角,从而可根据流动双折射测量结果定量计算聚合物熔体在挤出口模内的应力分布.

1 测量原理

传统实验装置中,一对互相垂直的1/4波片的作用是将平面偏振光变为圆偏振光,从而消除图像中的等倾线.文中为了得到取向角信息,特意去掉后面一个 1/4波片,组成新的双折射实验装置,如图 1所示.

图1 双折射实验装置原理图Fig.1 Schematic diagram ofbirefringence experiment

装置中起偏镜与检偏镜的偏振轴方向分别垂直、平行于 x轴方向,1/4波片的快轴方向与 x轴成45°角,将待测试样置入该光学系统中,从检偏镜出射的光矢量表达式为

式中:E为入射光的琼斯矢量;各光学元件的琼斯矩阵分别为

式中:δ、θ分别为待测模型产生的相位差与取向角.

经计算得出射光的强度为

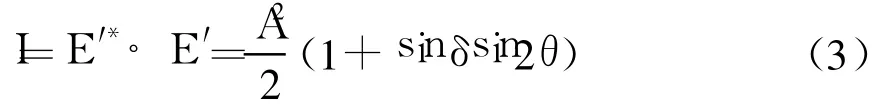
式中:A为入射光波的振幅.

分析式(3)可得:

(1)当sinδsin2θ=1时,光强I取得最大值.因为那么此时sinδ=1且 sin2θ=1,或者sinδ=-1且sin2θ=-1.这就说明当取向角θ为45°且相位差或者取向角 θ为-45°且相位差,出射光最强.

(2)当sinδsin2θ=-1时,光强取得最小值, I=0.此时sinδ=-1且sin2θ=1,或者sinδ=1且sin2θ=-1.也就是说当取向角θ为45°且相位差时者取向角θ为-45°且相位差δ=2k+,出射光最弱,为消光状态.

(3)对称流场中应力和取向角的值也呈轴对称分布,因此所测得的条纹图像信息关于对称轴反对称.

(4)不同的明暗条纹是由相位差引起的,单个条纹的亮度变化是由取向角的不同引起的.

(5)可以证明,把光学镜片同步旋转 90°,或者仅把 1/4波片旋转 90°,都可以实现类似的测量效果;同理,去掉第二个 1/4波片(保留第一个 1/4波片)也能得到类似结果.

由上述讨论可知,图像明暗条纹中既有相位差信息(等差线),又包含部分取向角信息.即光强最大或消光部分的取向角为 45°(或正或负),其符号可根据实际的流动情况判定.对于平面对称收缩流,对称轴以上流场的取向角一般介于 0°～-90°之间,相反在对称轴以下,取向角介于 0°～90°之间,因而,可以确定图像中最亮和最暗部分的取向角.

2 测量过程

文中利用如图 2所示的自制的突变收缩狭缝口模进行实验研究,挤出口模尺寸如下:型腔高度2H=20mm,狭缝高度2h=2mm,型腔厚度(z方向) D=25mm,狭缝出口宽高比(D/2h)=12.5.挤出原料为中国石化茂名分公司生产的LDPE1810D(密度为0.920 g/cm3,熔融指数为0.25).挤出机采用华南理工大学聚合物新型成型装备国家工程研究中心自行研制的 SDJJ-260型塑料电磁动态塑化挤出机,从挤出机加料口到口模的 4个加热段温度分别为145、165、170和 175℃,螺杆转速为 15r/min,平均流率为20.7g/min,口模死角处压力表显示为10.2MPa.

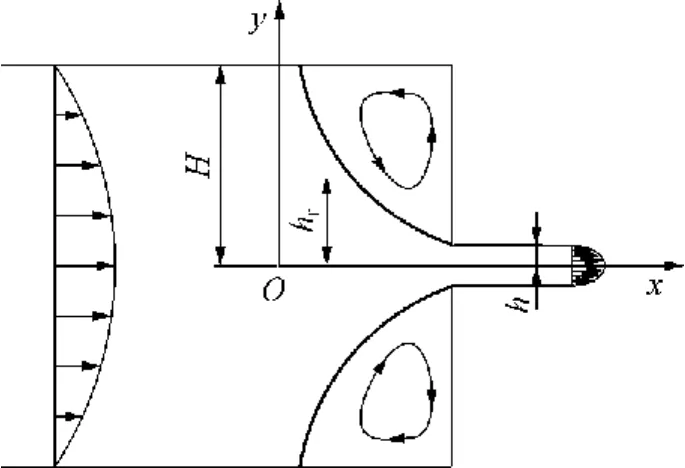
图2 突变收缩流道狭缝口模示意图Fig.2 Schematic diagram of abrupt contraction slitdie

实验采用He-Ne激光作光源,波长 =632.8nm.实验前首先利用对径受压圆盘,调整起偏镜与检偏镜,使其偏振轴相互垂直,并使检偏镜的偏振轴与熔体流动方向一致(水平方向).然后调整两个1/4波片,使其快轴相互垂直,且与流动方向成 45°角.在应用新的光学系统测量时,去掉前面一个 1/4波片即可.

文中在相同挤出条件下,分别用传统实验装置与新装置进行了实验,测量的图像如图3所示.

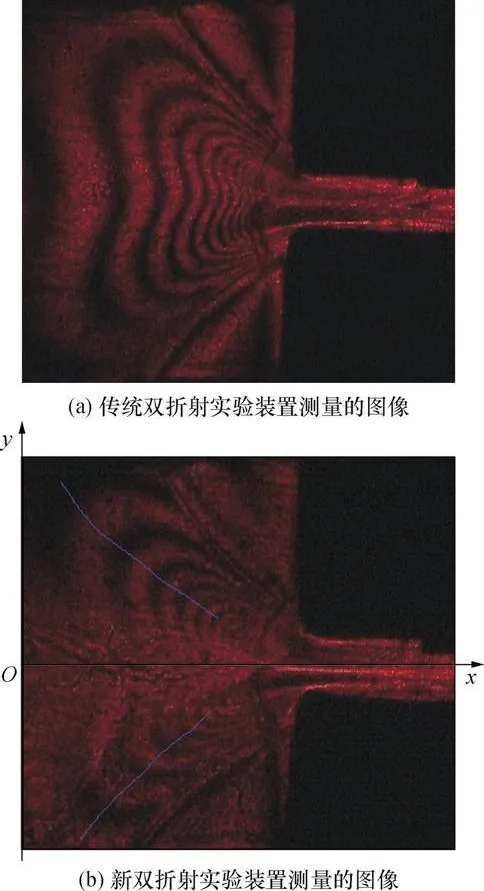
图3 不同实验装置测量的流场双折射图像Fig.3 Images obtained from different equipment of birefringence experiment

由图3(a)可见,应用传统双折射实验装置所测的条纹图像中,由于没有包含取向角信息,因而不能用来计算流场的应力状态;只有在假定对称轴上的取向角为 0°时,可根据对称轴上相应点的相延迟得到拉伸应力.由图3(b)所示的新实验装置得到的条纹图可见,该图关于对称轴呈反对称分布,即对称轴上面的暗条纹与下面的明条纹对应,这是因为其相位差相等而取向角的符号相反;图像中明暗相间的条纹为等差线,其相位差根据条纹级数计算得到.因而可由图3(b)直接计算45°等倾线上的应力分布.

由上述分析可知,图3(b)中最暗的部分的取向角为45°(对称轴以下)或-45°(对称轴以上),把图中最暗和最亮部分用平滑曲线相连,即得到 45°等倾线.对于流场中其他地方的取向角,将偏振镜和1/4波片同步顺时针旋转一定角度(如 5°),可得到-50°等倾线(对称轴以上)和 40°等倾线(对称轴以下).对于对称流场,由对称性可画出对称轴以下50°等倾线和对称轴以上 -40°等倾线.依次旋转,即可得到整场的取向角分布.

3 测量结果

首先根据所得图像信息,查出待测点处的干涉条纹级数,根据条纹级数确定相应的相位差(δ),然后根据相位差与折光率差(Δn)之间的关系(δ=算出折光率差,再根据应力 -光学定律(Δn=C×Δσ)计算出该点的主应力差Δσ[7].文中首先采用压差法计算应力光学系数,详细的计算方法参见文献[10]和[12],此处C=1.95×10-9m2/N.

通过对测量图像的观察分析,画出流场中取向角为45°的等倾线,如图 3(b)中所示蓝色线,文中以实际型腔中对称轴为 x轴,距离狭缝38mm处取作坐标原点.

有了待测部分的相位差 δ,可计算主应力差Δσ.再由取向角θ,根据公式(4)和(5)即可计算相应的剪切应力及第一法向应力差[7].图 4为沿等倾线上的剪切应力分布,由于取向角 θ=45°,此处的法向应力差为0.

式中:xy为流场剪切应力;xx-yy为法向应力.

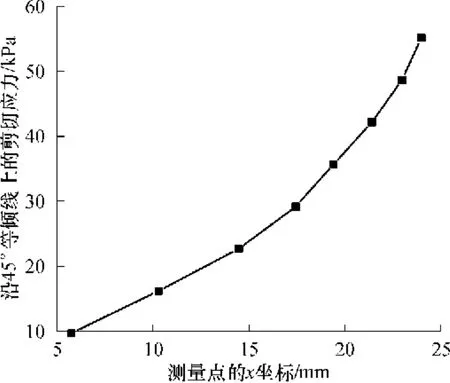
图4 45°等倾线上的剪切应力分布Fig.4 Shear stress along the 45°isoclinic line

由图4可知,随 x值增加,沿45°等倾线上的剪切应力急剧增加.由于该实验所用口模为收缩比为10∶1的突变收缩流道,聚合物熔体在死角处形成较大的涡流区,同时,熔体在对称轴上的流速(vy=0)呈加速趋势[11,13].对于任一给定的 x值,已知对称轴上的流速vy=0最大,而流型边缘(假设无滑移)的流速接近0.假设流场在y方向上的速度梯度∂vy/∂y为常数,那么其值即为vy=0/hf,因此随x值增加,熔体流动高度hf急剧变小,vy=0快速增加,那么熔体在y方向的速度梯度也急剧增大,所以,流场中的剪切应力也相应增大.因而,随着 x值增加,沿 45°等倾线上的剪切应力也呈加速上升趋势.

4 结语

文中对传统双折射实验装置进行了改进.为使实验测量得到的图像信息中包含取向角信息,在传统实验装置基础上去掉一个 1/4波片,并且通过合理布置偏振镜与波片,使 1/4波片的快轴方向与流动方向和起偏镜的偏振方向成 45°夹角,所得图像在光强最大或最小处的取向角为 45°,从而方便地计算 45°等倾线上的剪切应力.实验证明,该实验装置能用于测量聚合物流场中的应力分布,克服了传统双折射装置只能用于测量对称流场中对称轴上应力分布的缺陷.

文中还应用自制的可视化挤出口模,对LDPE1810D材料进行了实验测量,分析了实际生产条件下流场中的取向角和应力分布,为生产工艺的制定及优化和制品性能的改善提供了必要的数据.

[1] Cogswell F N.Converging flow of polymer melts in extrusion dies[J].Polymer Engineering and Science,1972,12 (1):64-73.

[2] Tanner R I.The theory of die swell[J].Journal of Polymer Science,Part A-2:Polymer Physics,1970,8(12): 2067-2078.

[3] Liang JZ.A relationship between extrudate swell ratio and entry stored elastic strain energy during die flow of tyre com pounds[J].Polymer Testing,2004,23(4):441-446.

[4] White S A,Gotsis A D,Baird D G.Review of the entry flow problem:experimental and numerical[J].Journalof Non-New tonian Fluid Mechanics,1987,24(2):121-160. [5] Rothstein JP,McKinley G H.The axisymmetric contraction-expansion:the role of extensional theology on vortex growth dynam ics and the enhanced pressure drop[J]. Journal of Non-Newtonian Fluid Mechanics,2001,98(1): 33-63.

[6] Janeschits-Kriegl H.Ploymermelt rheology and flow birefringence[M].New York:Springer-Verlag,1983.

[7] 赵清澄.光测力学教程 [M].北京:高等教育出版社, 1996.

[8] Quinzani LM,Armstrong R C,Brown R A.Birefringence and laser-doppler velocimetry studies of viscoelastic flow through a p lanar contraction[J].Journal of Non-Newtonian Fluid Mechanics,1994,52(1):1-36.

[9] White S A,Baird D G.Flow visualization and birefringence studies on planar entry flow behavior of polymer melts[J].Journal of Non-Newtonian Fluid Mechanics, 1988,29(1):245-267.

[10] Martyn M T,Groves D J,Coates P D.In process measurement of apparentextensional viscosity of low density polyethylenemelts using flow visualization[J].Plastics, Rubber and Composites,2000,29(1),14-22.

[11] Martyn M T,Groves D J,Coates P D.Stress measurements for contraction flows of viscoelastic polymermelts [J].Journal of Non-New tonian Fluid Mechanics,2000, 91(2):123-142.

[12] 金日光.高聚物流变学及其在加工中的应用 [M].北京:化学工业出版社,1986.

[13] Gough T,Spares R,Coates P D.In-process measurements of full field stress birefringenceand velocities in polymer melt flows[J].Plastics,Rubber and Composites,2005, 34(9):393-402.