基于图论技术的FPGA资源管理算法*

张宏烈 张国印

(1.哈尔滨工程大学计算机科学与技术学院,黑龙江哈尔滨 150001; 2.齐齐哈尔大学计算机与控制工程学院,黑龙江齐齐哈尔 161006)

可重构计算是一种兼有硬件的计算速度和软件的灵活性的计算模式,它能够有效提高系统的计算能力,因此在许多领域特别是嵌入式系统领域有着广阔的应用前景.随着可重构技术被关注程度的提高,面向应用的体系结构研究也越来越受到重视,研究面向应用的体系结构的一个重要课题就是可重构系统,即由一个主处理器和可重构逻辑器件(如FPGA)组成的系统.在可重构系统尤其是运行时可重构系统的应用中,由于FPGA具有动态可重构能力,可重构硬件资源的实时变化带来了新的问题.为了解决任务在FPGA上的布局/调度,可重构硬件资源的动态分配和管理成了近年来的研究热点.

可重构资源管理的重点是对空闲区域的管理.从 20世纪 80年代开始,不少学者提出了一些有效的空闲区域管理方法,现行的方法可以归纳为三类:不重叠空闲矩形列表,最大空闲矩形列表和顶点列表[1-2].Bazargan等[3]首先提出了互不交迭的空闲矩形的可重构资源管理方法,Walder等[4]通过延迟空闲矩形的形成和采用二维Hash函数对其进行了改进,该方法在大多数情况下不能标识出可重构硬件中的最大空闲区域,因此为任务分配资源时的成功率会受到较大影响.

与不重叠空闲矩形列表相比,使用最大空闲矩形列表管理空闲区域,资源利用率较高,但是寻找可重构芯片中最大空闲矩形的完全集却很耗时. Handa等[5]提出了阶梯算法来寻找最大空闲矩形的完全集,但存在时间复杂度高的问题;Cui等[6]提出了基本扫描线算法,该算法仍存在冗余计算和重复计算的问题.在已有的方案中,李涛等[7]提出的基于任务上边界计算最大空闲矩形的算法,由于链表的更新和任务的运行过程并发,故系统的计算性能得到了提高.

对于相互连通的空闲区域,可以采用位于空闲区域边界上的所有顶点构成的链表来管理所有的空闲资源.由于任务的动态添加和删除,使得顶点链表的管理和查找比较复杂.

针对现有算法存在的一些问题,文中将无向图与FPGA区域模型有机结合,提出基于虚拟无向图计算最大空闲矩形的新方法(KAMER_VU).该算法采用在虚拟无向图中寻找有效回路和通路的手段间接完成寻找最大空闲矩形的任务;在算法的实现过程中,不以任务已占用区域的上边界或顶点为基准,较好地改善了冗余计算和重复计算的问题,缩短了算法的有效损耗时间.

1 FPGA区域模型

任务如何布局到FPGA的空闲区域,FPGA的空闲区域如何管理,取决于FPGA的资源模型.文中将FPGA看作是二维阵列,采用二维区域模型.FPGA区域模型描述为:FPGA可看作是由W列H行基本配置逻辑单元CLB(Configurable Logic Block)构成的矩形区域模型,W、H分别是可重构芯片单行、单列具备CLB的个数,如图1所示.在该模型中,每个单元的位置编号假设为(i,j),其中1≤i≤W,1≤j≤H;每个单元的使用状态有两种:空闲状态和占用状态,若存在多个CLB单元连续空闲的情况,所形成的区域称为空闲连通区域.图 2中的空白区域即为空闲连通区域.

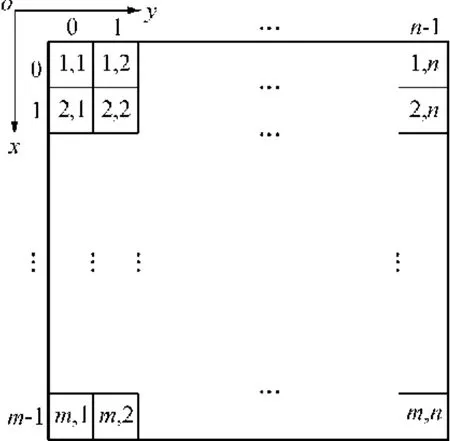
图1 FPGA区域模型Fig.1 FPGA region model

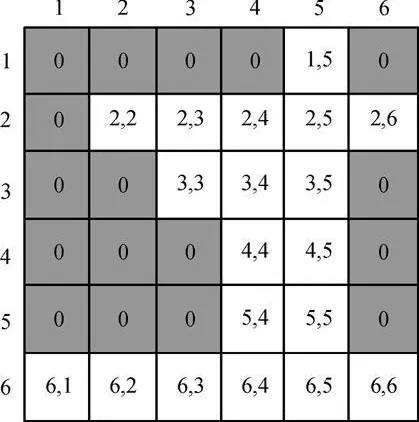
图2 空闲连通区域Fig.2 Free connected region

2 无向图与FPGA空闲区域的映射关系

无向图是一个有序二元组G=(V,E),对于FPGA资源的空闲区域,假设存在以下映射关系:

(1)一个CLB块映射为无向图的一个顶点;

(2)两个CLB块的相邻关系映射为无向图的一个边.

若空闲区域内部CLB块不予考虑,可以将空闲区域边界映射成一个无向图,且该无向图是由若干条水平和垂直通路构成的规则连通图.以图 2为例,其对应的无向图如图3所示,用Cij来表示位置编号为(i,j)的CLB块对应的顶点.

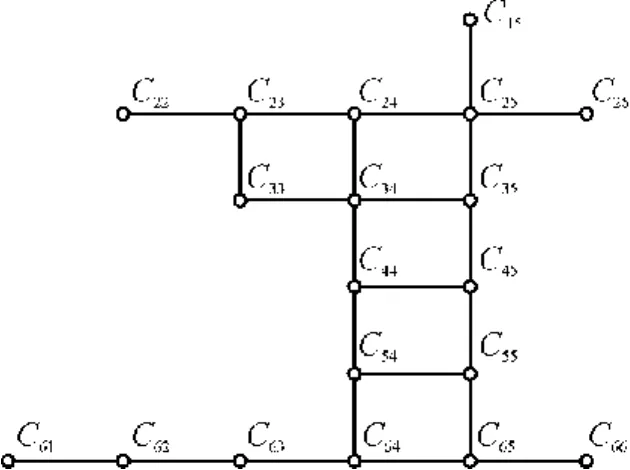
图3 空闲区域映射的无向图Fig.3 Undigraph of free regionmapping

将FPGA空闲区域映射成无向图后,在FPGA空闲区域寻找最大空闲矩形的问题转化为在无向图中寻找最大矩形的问题.

根据前面的分析可知,最大空闲矩形列表法是对空闲区域管理的最有效方法.采用适当的算法在空闲区域中可以搜索到若干最大空闲矩形,为任务布局提供快速的分配方案.

定义1(最大空闲矩形) 不能被其它任何一个空闲矩形所完全覆盖的空闲矩形为最大空闲矩形(MER).可用4维向量mer(x,y,w,h)描述,其中(x,y)代表MER左下角的CLB的位置编号,w、h分别代表MER的宽和长.

在图 2中符合最大空闲矩形定义的集合中包含5个MER,分别是(2,2,5,1)、(6,1,6,1)、(6,5,1, 6)、(3,3,3,2)、(6,4,2,5).集合中的最大空闲矩形构成可以归纳为两大类:一类是单排或单列结构,即最大空闲矩形是由若干个CLB块一字排列构成,如(2,2,5,1)、(6,1,6,1)、(6,5,1,6),该类最大空闲矩形映射到无向图中,对应一条水平或垂直通路;另一类是矩形结构,即最大空闲矩形是由若干排若干列 CLB块构成,如(3,3,3,2)、(6,4,2,5),该类最大空闲矩形映射到无向图中,对应一个回路.从以上映射关系中可以得出一个结论:寻找最大空闲矩形的问题在无向图中转化为寻找满足条件的回路和通路的问题.

3 KAMER_VU算法

KAMER_VU算法根据虚拟无向图计算和保持最大空闲矩形.设G=(V,E)是一个虚拟无向图,为G中n个顶点的集合,顶点Vs的坐标为(i,j),即CLB块的位置编号.若V1,V2,…,VK是V中K个连续顶点,则有定义如下.

定义2(水平通路) 对于所有1≤s≤k满足Vs纵坐标取值相等,则G中V1,V2,…,Vk构成的通路称为水平通路.在图 3中,就是两个水平通路.

定义3(垂直通路) 对于所有1≤s≤k满足Vs横坐标取值相等,则G中V1,V2,…,Vk构成的通路称为垂直通路.在图 3中,就是两个垂直通路.

对于连通的虚拟无向图而言,图中只有一个最大回路,即能包容全部度数为 2的顶点和边的回路,如图 3所示,最大回路是.

定义4(最长水平通路) 水平通路中经过的所有顶点不完全是最大回路中的顶点.如图3中,V=是最长水平通路.而 C61、C62、C63、C66不是最大回路中的顶点.

定义5(最长垂直通路) 垂直通路中经过的所有顶点不完全是最大回路中的顶点.如图3中,V=是最长垂直通路,但 C15不是最大回路中的顶点.

进一步分析可得:最长水平通路和最长垂直通路“逆映射”到FPGA中,恰恰就是具有单排或单列结构的最大空闲矩形;最大回路可以按照扫描方法得到若干个部分重叠的子回路,该子回路“逆映射”到FPGA中,恰恰就是具有若干排若干列CLB块构成的最大空闲矩形.图 3中构造两个部分重叠的子回路对应两个最大空闲矩形.

基于虚拟无向图计算最大空闲矩形的算法流程如图 4所示.在图 4的算法中,搜索最大回路是算法的一个关键,最大回路的搜索过程分为3个步骤.

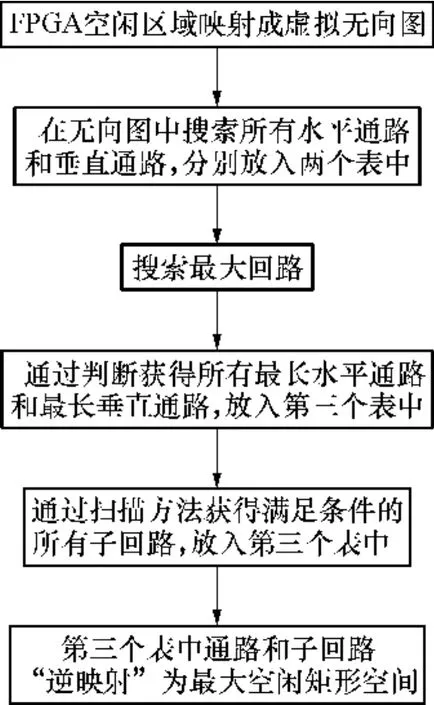
图4 KAMER_VU算法流程图Fig.4 Flowchartof KAMER_VU algorithm

3.1 无向图的预处理

在由相关顶点和边构成的无向图中,每个顶点的度数都为 2的连通图称为回路.因此,图 3中需要将度数为 1的悬挂顶点以及与它关联的悬挂边裁剪掉,连续进行裁剪后,得到图5所示的无向图.

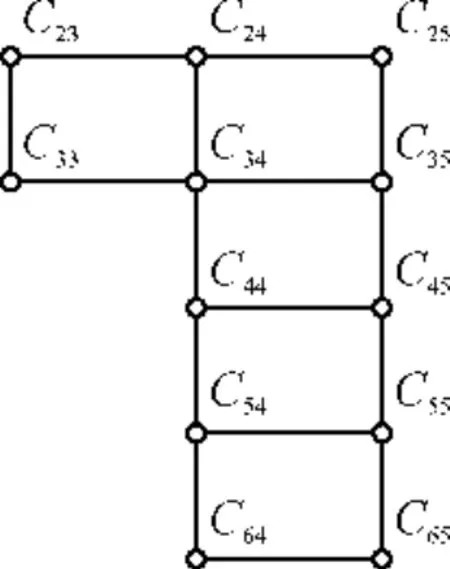
图5 预处理后的无向图Fig.5 Preprocessed undigraph

3.2 建立无向图邻接矩阵

根据图5建立邻接矩阵M 1,由于邻接矩阵是对称方阵,存储时只需存储矩阵的上三角矩阵.

3.3 搜索最大回路

对于连通的无向图,最大回路只有一个.引入方向矢量交角[8],可以在无向图中很快找到最大回路,具体搜索过程如下:

(1)确定搜索出发点和起始边.假设无向图上全部顶点均有相应坐标,搜索出 x坐标最小的顶点,即最左边的某一顶点作为搜索的出发点,在图 5中是顶点C23.根据邻接矩阵,求该点邻接边相对于x轴的方向矢量交角,找出方向矢量交角最小的边＜C23,C33＞作为搜索起始边,该边必然为最大回路中的一条边,将邻接矩阵 M 1中对应元素 M141减 1, C33作为下一次搜索的起始顶点.

(2)搜索与当前搜索边相邻的所有边.根据邻接矩阵M 1和顶点坐标,求与顶点C33的所有邻接边相对于当前搜索边 ＜C23,C33＞的方向矢量交角,找出方向矢量交角最小的边 ＜C33,C34＞,该边也一定是最大回路的一边,将邻接矩阵 M 1中对应元素M154减 1.搜索出的边 ＜C33,C34＞作为下次搜索的起始边,该边的终点C34作为下次搜索的起点.

(3)重复步骤(2),直到搜索边的终点回到出发点为止,邻接矩阵演化为 M 2,所形成的回路即为最大回路,如图6所示,即

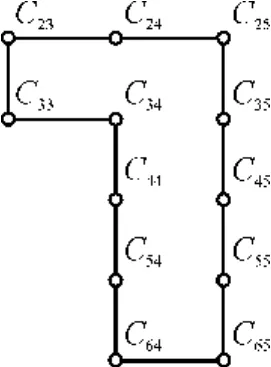
图6 最大回路Fig.6 Themost large loop

4 仿真

为了测试KAMER_VU算法的性能,文中在一个FPGA仿真环境中进行实验,仿真环境最小时间单位为10ms,大小为96×64个CLB块.任务生成器随机产生20000个硬件任务,存储在队列里,硬件任务的宽度和长度范围是 2到8个 CLB,布局器根据First Fit(FF)适应策略为到达的硬件任务选择合适的最大空闲矩形.分别采用KAMER_VU算法与SL (Scan Line)算法仿真,结果如表1所示.

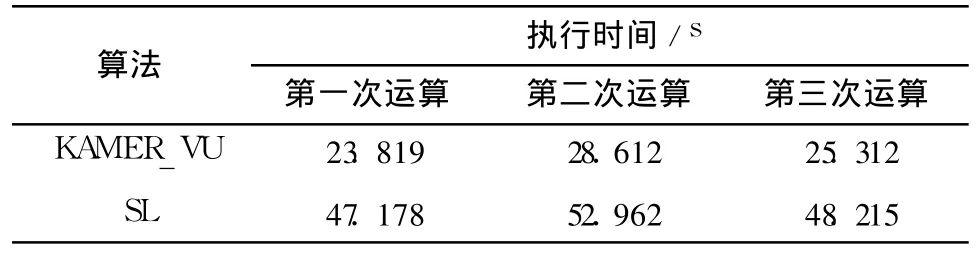
表1 KAMER_VU算法与SL算法的执行时间Table1 Execution time of KAMER_VU and SL algorithms

由表1可见,KAMER_VU的平均执行时间约为SL算法的 1/2.由此可以判断,由于扫描线算法有冗余计算的问题,随着可重构芯片规模的增长,KAMER_VU的优势将更明显.

文献[9]中给出了任务拒绝率TRR,执行时间PT和有效耗损时间VCT等概念,且VCT是TRR和PT之积.由定义可知,当任务拒绝率高而且执行时间长的时候,有效耗损时间就长.分别触发不同数目的硬件任务,测试KAMER_VU算法和SL算法的VCT,结果如图7所示.由图7可知,KAMER_VU算法的VCT是SL算法的60%左右,性能更优.

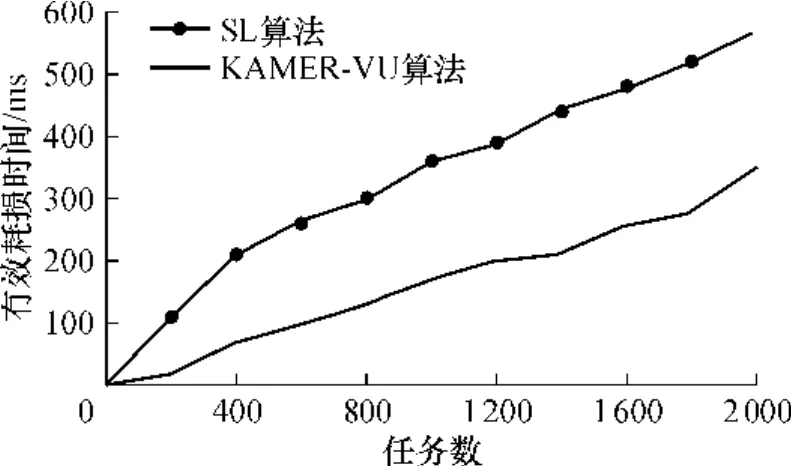
图7 KAMER_VU算法和SL算法的VCT值Fig.7 VCT values of KAMER_VU and SL algorithms

5 结语

文中利用FPGA资源模型特征,将无向图与FPGA模型有机结合,分析了二者之间的映射关系,提出了基于虚拟无向图计算最大空闲矩形的算法.该算法将寻找最大空闲矩形问题转化为求解有效回路和通路的问题,使空闲区域划分过程大大简化.仿真结果表明,应用KAMER_VU算法解决问题是可行的,且该算法的性能优于SL算法.

将图论技术应用于可重构资源管理领域,目前在国内报道不多,文中在这个方面进行了初步探索,且仿真结果比较理想,但在算法结构和计算复杂度等方面还存在不足,有待于进一步改进.

[1] Tabero J,Step tien J,Mecha H,et al.Task placementheuristic based on 3D-adjacency and look-ahead in reconfigurab le systems[C]∥Proceedings of the 11th Asia and South Pacific Design Automation Conference 2006.Yokohama:IEEE Circuits and Systems Society ACM SIGDA, 2006:169-174.

[2] 齐骥,李曦.基于硬件任务顶点的可重构系统资源管理算法[J].电子学报,2006,34(11):2094-2098.

Qi Ji,LiXi.Algorithms of resourcemanagement for reconfigurable systems based on hardware task vertexes[J]. Acta Electronica Sinica,2006,34(11):2094-2098.

[3] Bazargan K,Kastner R,Sarrafzadeh M.Fast temp late placement for reconfigurable computing systems[J].IEEE Design and Testof Computers,2000,17(1):68-83.

[4] Walder H,Steiger C,Platzner M.Fast online task p lacment on FPGAs:free space partitioning and 2D hashing [C]∥International Parallel and Distributed Processing Symposium.New York:IEEE Computer Society,2003: 209-224.

[5] Handa M,Vemuri R.An efficientalgorithm for finding em pty space for online FPGA placement[C]∥Field Programmab le Logic and App lication:14th International Conference.Berlin:Sp ringer,2004:444-453.

[6] Cui Jin,Deng Qingxu,He Xiuqiang,et al.An efficient algorithm for online management of 2D area of partially reconfigurable FPGAs[C]∥2007 Design,Automation and Test in Europe Conference and Exposition.Nice: EDAA EDAC IEEE Computer Society TTTC,2007:129-134.

[7] 李涛,杨愚鲁.可重构资源管理及硬件任务布局的算法研究 [J].计算机研究与发展,2008,45(2):375-382.

Li Tao,Yang Yu-lu.Algorithms of recon figurab le resource management and hardware task p lacement[J].Journal of Computer Research and Development,2008,45(2):375-382.

[8] 付志红,俞集辉,苏向丰.引入方向因子的最小回路、最大回路搜索算法 [J].重庆大学学报:自然科学版, 2002,25(3):64-67.

Fu Zhi-hong,Yu Ji-hui,Su Xiang-feng.The algorithm of searching out the leastandmost loop bymaking use of direction factor[J].Journal of Chongqing University:Natural Science Edition,2002,25(3):64-67.

[9] 龚育昌,齐骥.一种支持动态可重构系统的布局碎片量化方法 [J].小型微型计算机系统,2007,28(5): 944-947.

Gong Yu-chang,Qi Ji.An app roach to quantify p lacement fragments for dynam ic recon figurable systems[J].Journal of Chinese Computer Systems,2007,28(5):944-947.