考虑频率特性的负荷模型研究及应用

张 孝，鞠 平，陈 谦，张 伟，于永军，祁晓笑，姚秀萍，孙宜谦，常喜强

(1.河海大学能源与电气学院，江苏南京 210098;2.新疆电力科学研究院，新疆乌鲁木齐 830000; 3.新疆电力公司，新疆乌鲁木齐 830000)

一般来说，电力系统中电压波动较大而频率波动很小，所以长期以来，电力负荷建模研究大都是围绕电力负荷的电压特性进行的，取得了丰硕的成果[1-8].但是，在某些薄弱的电网(比如新疆电网)，或者系统中发生特大干扰，系统的频率会存在一定幅度的波动.由于频率的变化，负荷功率将随之变化，这种负荷功率随频率变化的特性称之为负荷的频率特性，分为动态频率特性和静态频率特性.电力负荷的频率特性对于低频振荡、低频减载等具有重要影响[9]，有必要对负荷的频率特性进行研究.

有关电力负荷的静态频率特性已有一些研究[10-11]，一般需要进行专门的稳态频率试验，代价较大，频率调整很难;而对于动态频率特性，相关研究成果很少，因为动态频率变化很难捕捉.为此，本文提出了两种考虑频率特性的负荷模型以及“先动后静”获取静态特征系数的方法.

1 考虑频率的综合负荷模型

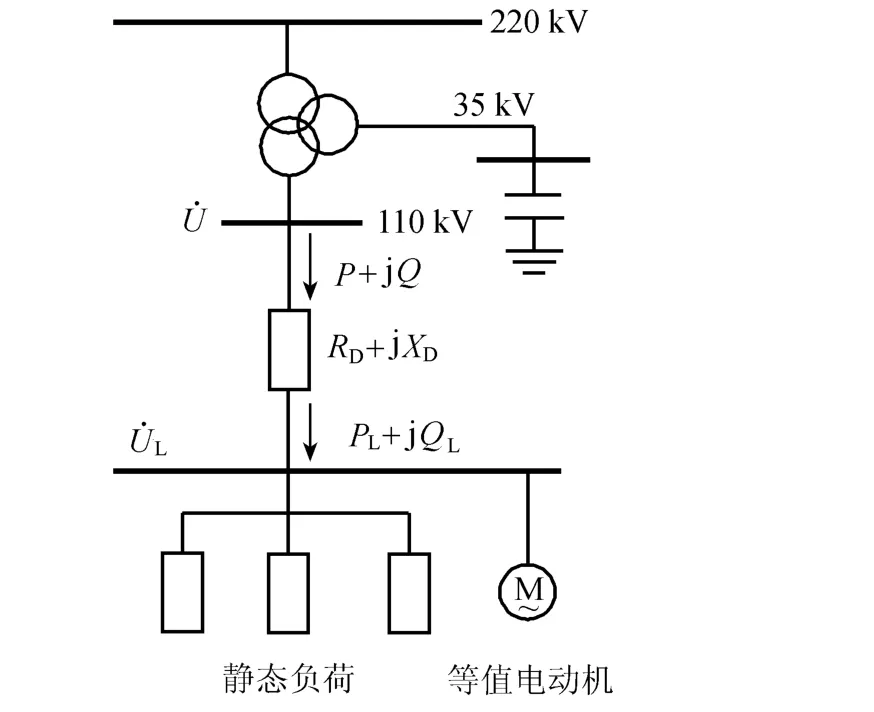
图1 综合负荷模型结构Fig.1 Structure of synthesis load model

由于电动机在电力系统负荷中占相当大的比例，并且对电力系统的分析和仿真有重要影响，所以综合负荷模型多采用电动机并联静态负荷然后串联配电网支路的模型结构[1]，即考虑配电网支路的综合负荷模型(synthesis load models，SLM)，如图1所示.

令实际负荷母线电压 ﹒U=U∠0°，由图1可以看出，配电网支路模型方程如下:

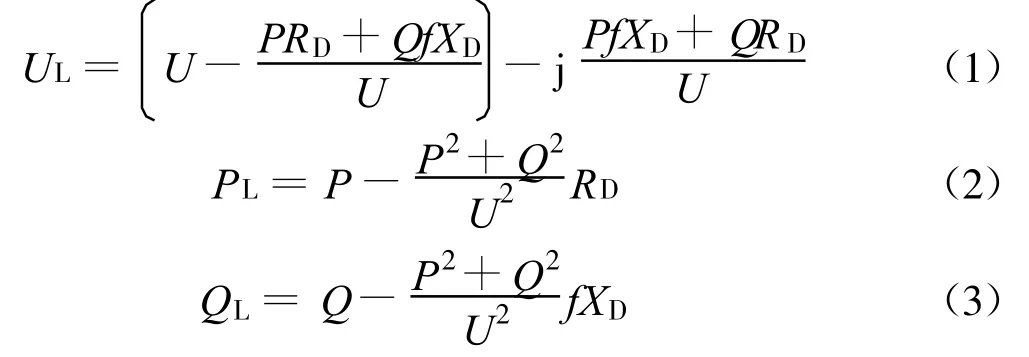
式中:P，Q，U，f——实际负荷母线上的有功功率、无功功率、电压和频率;PL，QL，UL——虚拟母线上的有功功率、无功功率和电压;RD，XD——配电网等值电阻和等值电抗.

对于综合负荷模型中的静态负荷部分，考虑频率特性的模型方程如下[12]:

式中:Ps，Qs——静态负荷消耗的有功功率和无功功率，下标0表故障前的量;pu，pf，qu，qf——静态特征系数.也可以采用多项式模型:

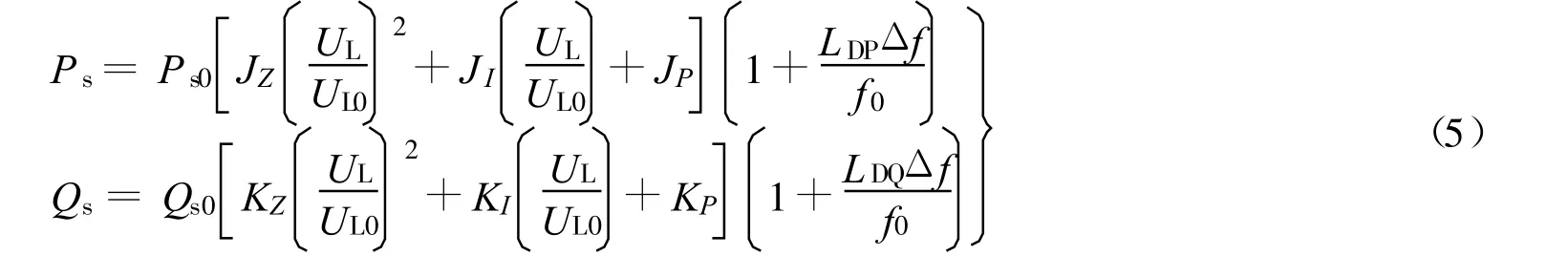
其中特征系数满足:

式中:JZ，JI，JP——有功负荷中恒阻抗、恒电流、恒功率所占的比例;KZ，KI，KP——无功负荷中恒阻抗、恒电流、恒功率负荷所占的比例;LDP，LDQ——有功频率特征系数和无功频率特征系数.

对于感应电动机部分，如果忽略电子绕组电磁暂态，则可获得三阶的机电暂态模型.该模型一般采用电抗而非电感，所以频率会涉及电抗和电压方程，由于篇幅所限，这里不进行详细推导，而直接给出模型方程(同步坐标下):

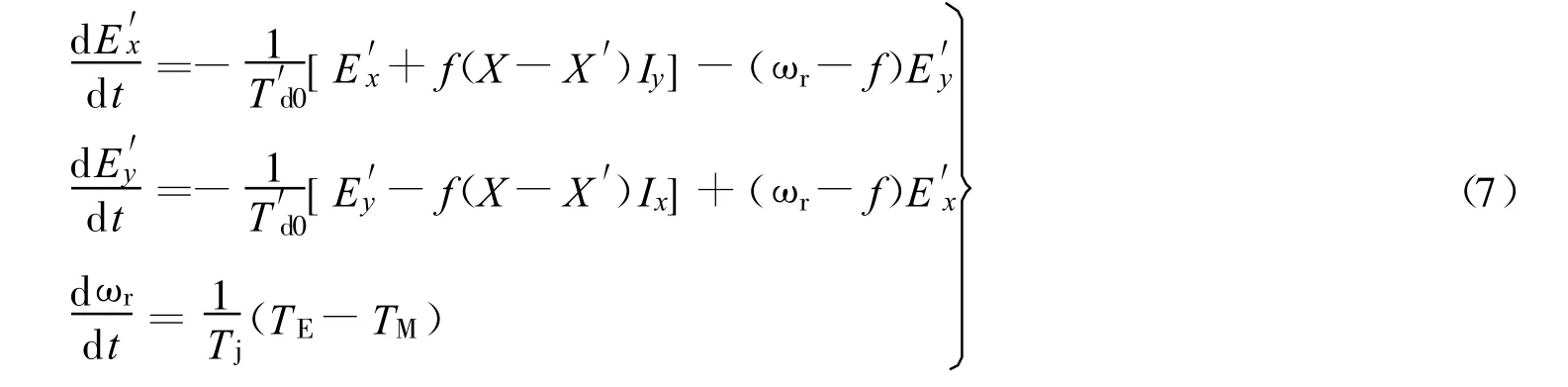
同步坐标下电压方程为

由式(8)可得考虑频率的感应电动机暂态等值电路如图2所示，转矩方程为

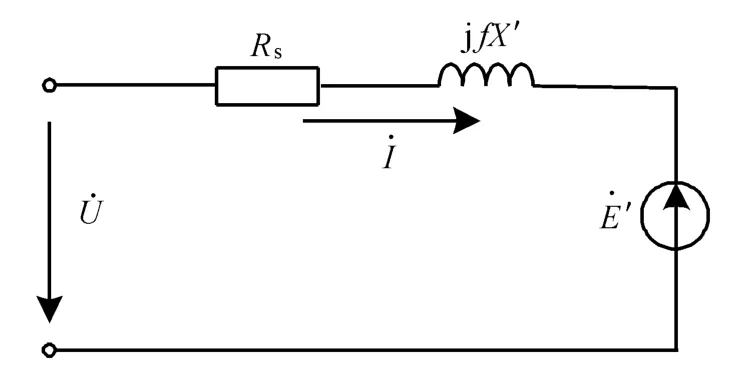
图2 考虑频率时电动机暂态等值电路Fig.2 Transient equivalent circuit of motor considering frequency

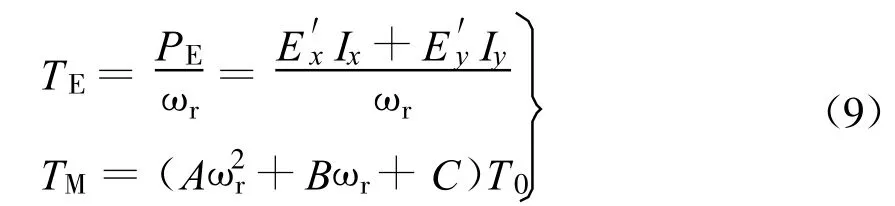
式(7～9)中:E′x，E′y——直轴和交轴电势;Ix，Iy——同步坐标下的定子绕组电流;ωr——转子转速;T′d0——定子开路时的转子回路时间常数;Tj——转子惯性时间常数;TE，TM——电磁转矩和机械转矩;T0——初始机械转矩;A，B，C——机械转矩系数(满足A+B+C=1);Rs——定子电阻;X，X′——正常频率f0下的稳态电抗和暂态电抗.

2 线性动态模型

电力系统电压和频率之间存在着紧密关系，频率变化时电压也会变化.一般来说，频率变化较小，因此可以采用线性化模型.

高阶线性动态模型可用传递函数表示为

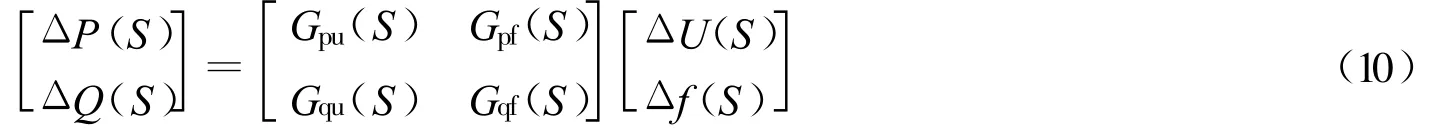
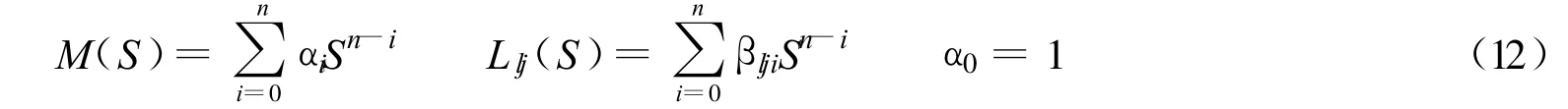
式中l表示p或q，j表示u或f.应注意，式(11)中各传递函数元素的分母是相同的，实际应用时也可以不同.

连续传递函数可以转换成如下离散传递函数

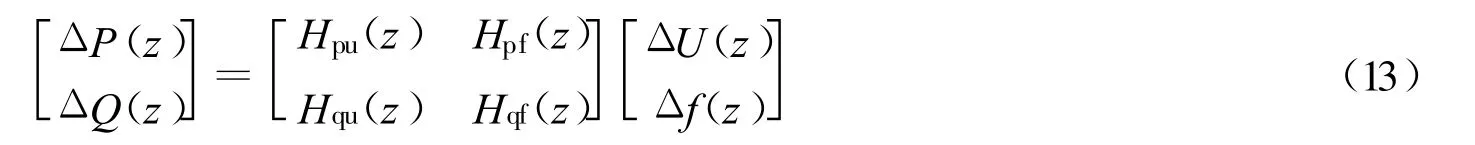
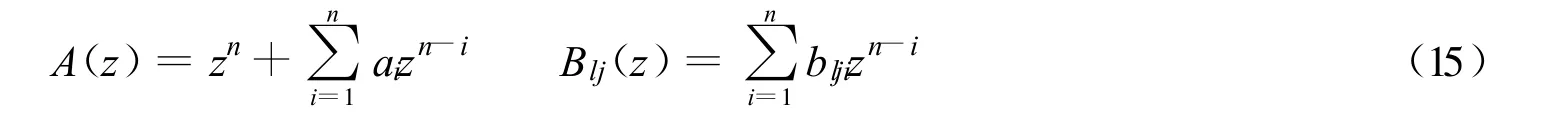
对应式(13)的离散差分方程式如下

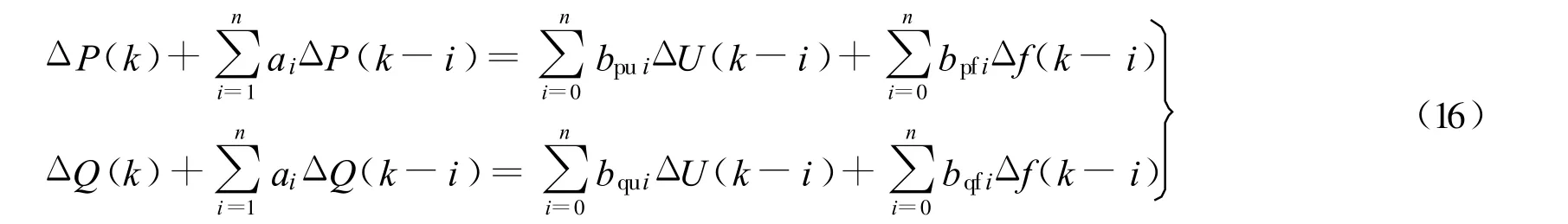
在进行参数辨识时，一般采用离散模型，因为计算机采集数据及处理数据时，所有的信号都是离散形式的.另一方面，离散差分方程在本质上是一种代数方程，因而比微分方程的处理要容易得多.式(16)中各系数可由最小二乘法(LSE)辨识得到，具体方法参见文献[12].

3 由线性动态模型确定静态特征系数

式(4)中静态特征系数pu，pf，qu，qf是用于反映负荷静态特性的，可由统计综合法或由稳态试验法确定，但是这两种方法都要花费大量的人力与物力，而在线采集数据并辨识负荷特征系数是解决负荷时变性问题的可取途径.对于真正的静止型负荷，可采用静态模型去拟合并确定静态特征系数.但是，对于包含动态成分的负荷，如果仍用静态模型去拟合，将产生较大误差.严格来说，一个变电站下面的负荷群或多或少都会包含动态成分，因而应将负荷看成动态系统，即采用动态模型去描述负荷.另外，采用线性动态模型既可以获得负荷的动态特性模型，又可以很方便地由动态特性模型得到负荷的静态特性模型.

所谓静态特性是指负荷在稳态条件下所呈现出的特性.在稳态条件下，当电压及频率与初始值偏移很小时，可将模型线性化

根据负荷的物理本质可知:在稳态条件下，动态模型应退化为静态模型.所谓稳态条件，也就是动态方程中各变量导数为零，令S=0(对应连续传递函数)或z=1(对应离散传递函数).将z=1代入式(13)可得

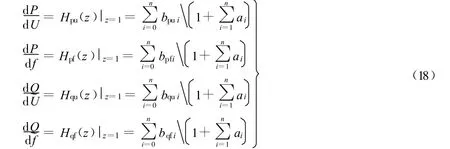
于是静态特征系数的估计值为

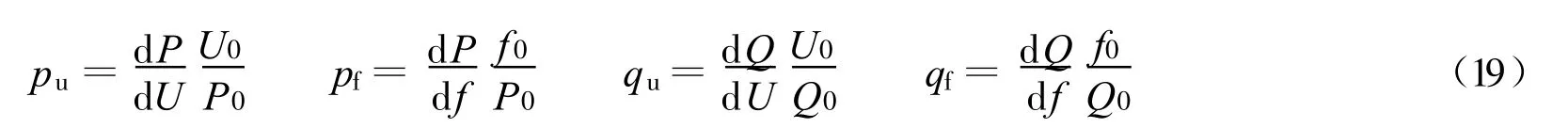
由此可见，由线性动态模型可以很方便地获得静态特征系数，计算公式非常简单，几乎不增加多少计算量.这样，就可以不进行专门的稳态频率试验，节省大量的人力和物力.由于是先根据频率动态小扰动数据辨识动态模型，再放到稳态条件下获得静态特征系数，所以称之为“先动后静”方法.

4 算例应用

在新疆电网实际测量数据中，挑选出频率波动较大的1组(鲤鱼山2号主变某次扰动数据)作为示例(以下相关数据均为标幺值)，电压、频率实测值如图3所示，可见频率波动幅度约1.4%，电压波动幅度约13%.

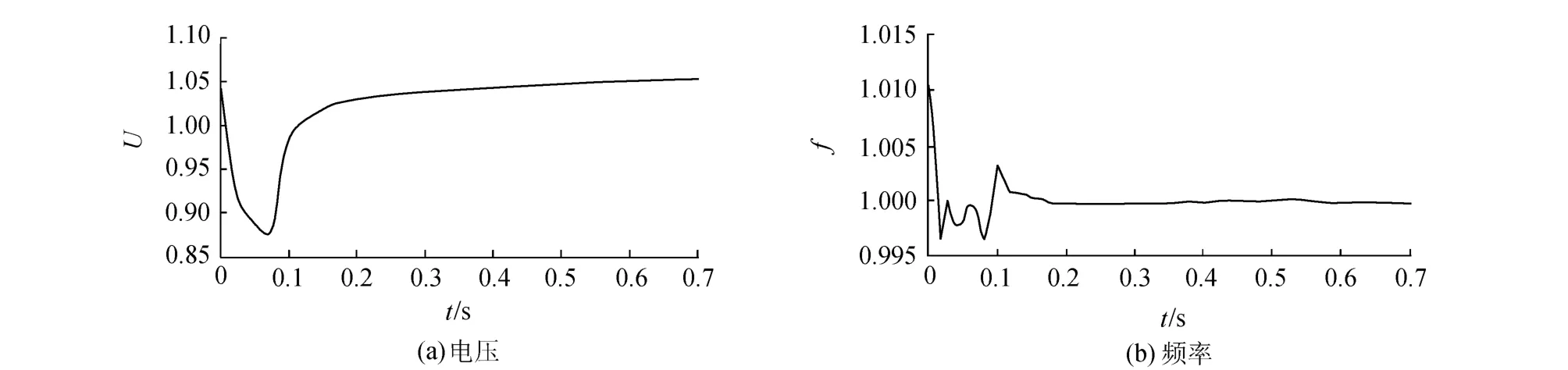
图3 实测电压和频率Fig.3 Measured voltage and frequency

4.1 不同阶次模型的比较

在考虑频率特性的情况下，分别采用不同阶次的线性动态模型，辨识参数并且计算其动态响应如图4所示.由图4可见，三阶线性动态模型比较合适，据此所得静态特征系数为pu=0.573，qu=2.374，pf=0.527，qf=-2.944，误差为0.0017.

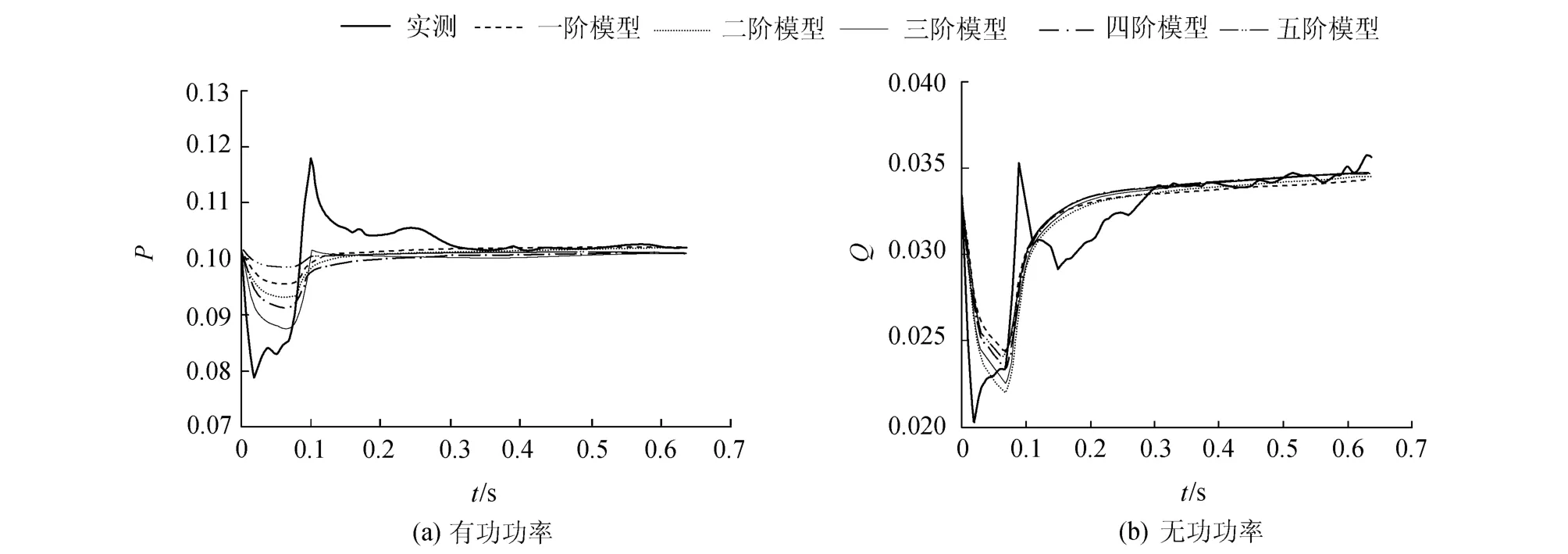
图4 各阶线性动态模型比较Fig.4 Comparison between different linear dynamic models

4.2 考虑频率与否的比较

在考虑与不考虑频率两种情况下，分别采用线性动态模型和综合负荷模型，辨识所得参数见表1和表2，对应的动态响应曲线对比如图5和图6所示，可见，采用线性动态模型时，考虑频率特性模型所得曲线明显好于不考虑频率特性模型;采用电动机综合负荷模型时，考虑频率特性模型所得曲线略好于不考虑频率特性模型.

表1 考虑频率与否的静态特征系数Table 1 Comparison of static characteristic coefficients with and without consideration of frequency

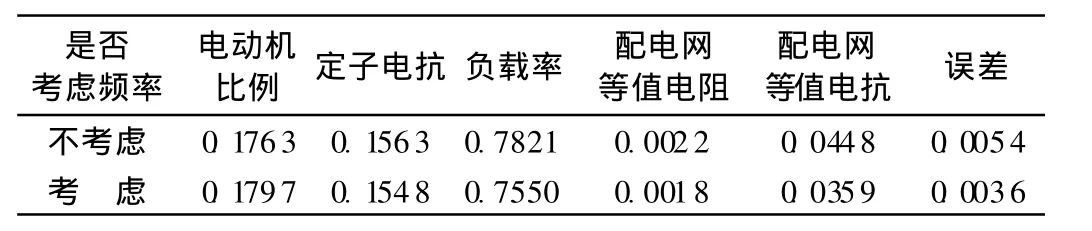
表2 考虑频率与否的重点电动机参数Table 2 Comparison of parameters for key motors with and without consideration of frequency

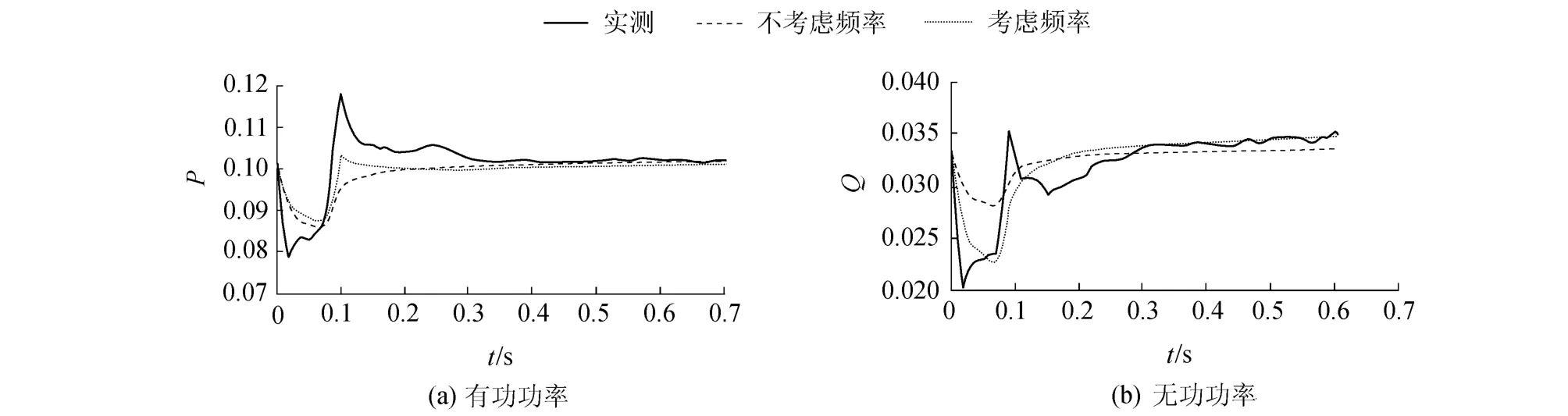
图5 三阶线性动态模型考虑频率与否动态响应Fig.5 Dynamic responses of third-order linear dynamics with and without consideration of frequency model

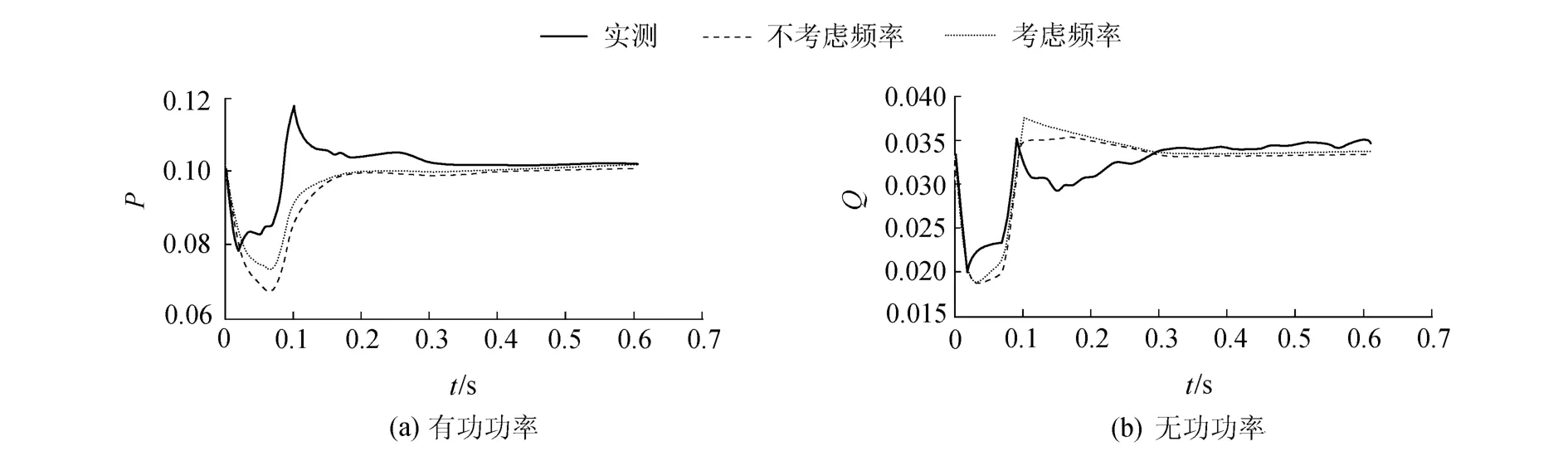
图6 电动机模型考虑频率与否动态响应Fig.6 Dynamic responses of motor model with and without consideration of frequency

5 结 论

a.综合负荷模型线性动态模型的动态响应都比较接近实测结果.

b.考虑频率比不考虑频率的动态拟合效果要好.

c.“先动后静”的方法可以很方便地由频率动态小扰动数据获得负荷的静态特征系数，大大简化了频率特性获取工作.

[1]汤涌，张红斌，侯俊贤，等.考虑配电网络的综合负荷模型[J].电网技术，2007，31(5):34-38.(TANG Yong，ZHANG Hong-bin，HOU Jun-xian，et al.A synthesis load model with distribution network[J].Power System Technology，2007，31(5):34-38.(in Chinese))

[2]张东霞，汤涌，朱方，等.接于高压母线的电动机负荷等值模型[J].中国电机工程学报，2006，26(6):14-18.(ZHANG Dongxia，TANG Yong，ZHU Fang，et al.Equivalent model for induction-motor load connected to high voltage bus[J].Proc f the CSEE，2006，26(6):14-18.(in Chinese))

[3]鞠平，谢会玲，陈谦.电力负荷建模研究的发展趋势[J].电力系统自动化，2007，31(2):1-4.(JU Ping，XIE Hui-ling，CHEN Qian.Research tendencies of electric load modeling[J].Automation of Electric Power Systems，2007，31(2):1-4.(in Chinese))

[4]PERERIRA L，KOSTEREV D，MACKIN P，et al.An interim dynamic induction motor model for stability studies in the WSCC[J].IEEE Trans PWRS，2002，17(4):1108-1115.

[5]MA Jin，HE Ren-mu，HILL D J.Load modeling by finding support vectors of load data from fieldmeasurements[J].IEEE TransPWRS，2006，21(2):726-735.

[6]杨华春，贺仁睦，王鹏，等.基于聚合理论的大区电网负荷建模[J].电力系统自动化，2005，29(1):49-52.(YANG Hua-chun，HE Ren-mu，WANG Peng，et al.Load-modeling in large-scale grid based on the aggregation theory[J].Automation of Electric Power Systems，2005，29(1):49-52.(in Chinese))

[7]李培强，李欣然，唐外文，等.统计综合法负荷建模中的行业用户精选[J].电力系统自动化，2005，29(14):48-52.(LI Peiqiang，LI Xin-ran，TANG Wai-wen，et al.Consumer choice for an industry in statistical synthesis method based load modeling[J]. Automation of Electric Power Systems，2005，29(14):48-52.(in Chinese))

[8]陈谦，黄文英，李成，等.电力负荷建模的在线统计综合方法[J].电力系统自动化，2008，32(2):8-10.(CHEN Qian，HUANG Wen-ying，LI Cheng，et al.Component basedon-line modeling of electric loads[J].Automation of Electric Power Systems，2008，32(2):8 -10.(in Chinese))

[9]鞠平，马大强.电力负荷的动静特性对低频振荡阻尼的影响分析[J].浙江大学学报:工学版，1989，23(5):750-761.(JU Ping，MA Daqiang.Effects of static and dynamic loads on damping of low-frequency oscillations in electric power systems[J].Journal of Zhejiang University:Engineering Science，1989，23(5):750-761.(in Chinesse))

[10]AKHTAR M Y.Frequency-dependent power system static load characteristics[J].IEEE Trans PAS，1968，115(9):1307-1314.

[11]WELFONDER E，WEBER H，HALL B.Investigations of the frequency and voltage dependence of load part system[J].IEEE Trans PWRS，1989，4(1):19-25.