基于两点估计法的电力系统静态电压稳定概率分析
2010-03-14侯学勇付红军
侯学勇,鞠 平,付红军
(1.河海大学能源与电气学院,江苏南京 210098;2.河南电力调度通信中心,河南郑州 450052)
长期以来,电力系统稳定性分析结果大部分是针对确定的网络结构、元件模型参数以及有限的运行工况通过确定性方法计算分析得到的.然而实际电力系统中存在着各种随机因素,系统工况中各种运行数据及其测量、系统的参数甚至干扰方式等都存在着不确定性.如果以确定性分析方法计算每种可能状态下的系统稳定性,计算量会非常庞大,这样既没有必要而且也不现实,因为在确定性分析中得出的稳定性评估结论一般是根据系统应对最严重的情况计算得到的,这样的结论往往过于保守.最终的结果是电力部门为了应对这种情况而浪费大量精力进行投资建设或人为地限制电网的输送容量等,不利于电网的经济运行.此外,确定性分析仅能给出系统稳定与否的结果,缺乏系统稳定概率和风险指标等统计信息,不利于电力部门对电网进行规划和决策.为此,人们自然就提出了电力系统概率稳定分析问题(PAS),即根据系统中影响稳定的主要随机因数的统计特性来确定电力系统的概率稳定指标[1-3].目前相关研究主要集中在静态稳定性概率分析[4]、暂态稳定性概率分析[5]、可用传输容量计算[6]、随机潮流分析[7]、电力系统风险或可靠性评估方法及指标研究[8-14]等几个方面.
为了克服传统确定性方法在电压稳定问题研究中存在的不足,需要掌握与电压失稳相关的一些概率统计信息以满足电力部门对电网决策规划以及经济运行的需要.文献[11]提出了基于负荷裕度随机特性利用半不变量方法来计算电压失稳概率;文献[12]在文献[11]基础上提出了一种含风电场的电力系统电压稳定概率分析的混合方法;文献[13]建立了以系统功率极限均值、母线与支路参与因子均值为代表的电压稳定概率指标,同时计及了节点负荷相关性和负荷预测不确定性,获得系统在一定负荷水平上的失稳概率,并确定了容易发生电压失稳的区域,为采取更加经济有效的措施来提高系统电压稳定性奠定了基础;文献[14]提出了一种负荷不确定性电网的电压稳定性评价方法,该方法提出了一种在负荷取值不确定条件下评估电网电压稳定性的数学模型,然后用边界定值法求解该模型,得到满足节点自身和总负荷波动范围约束的最恶劣负荷分布,并以此负荷分布下的最小负荷距离作为评价电压稳定性的指标,该指标在实际电网规划中具有比较重要的意义.
本文以简单两节点电力系统为背景,建立静态电压稳定概率分析模型,提出了基于两点估计(two-point estimate,TPE)法的概率静态电压稳定计算方法,并通过算例对该方法进行了验证.
1 静态电压稳定概率分析模型与方法
1.1 静态电压稳定的概率分析模型

图1 功率差曲线Fig.1 Curves of power difference
在静态电压稳定分析理论中,一般情况下都是以负荷裕度作为电压稳定的指标.从系统给定的初始运行点出发,通过某种形式的负荷增长或传输功率的增长可以逐步逼近并最终达到电压崩溃的临界点,则初始运行点到临界点之间的功率差额被定义为负荷裕度[15].由该定义可以看出,系统电压稳定的负荷裕度不仅与初始运行点和临界点的位置有关,还与事先设定的负荷增长方向有着密切的关系,而且该定义并未考虑到负荷静态电压特性在负荷增长过程中对电压稳定的影响.针对这一点,本文提出考虑负荷静态特性的静态电压稳定分析数学模型:以文献[16]中的分析为背景,图1给出了3种不同的稳定状态下的有功差值线,据此,定义静态电压稳定广义裕度指标,将图1中的有功差值线上拐点有功数值作为静态电压稳定裕度,称之为功率差裕度Kp,计算公式如下:

式中:p——由0~1间计算时间步长 Δ组成的向量;u——与 p对应的在发电侧曲面与负荷侧平面交线上的电压向量;A0,A1,A2——经类似标么化后的负荷侧系数[16].由图1可以看出,当Kp>0时系统静态电压稳定,Kp数值越大对应系统静态电压稳定裕度越高;当Kp<0时系统静态电压失稳,Kp数值越小对应系统静态电压稳定失稳越严重.
式(1)的结果是一个具体的数值,当系统中电源侧参数、功率水平和负荷模型参数都给定时,系统可以根据Kp是否大于0判断电压是否稳定.然而,由于系统实际运行中存在很多不确定因素的影响,比如电源侧参数中线路阻抗由于原来的双线运行因事故变成单线运行会导致系统与负荷之间的阻抗值加倍、负荷功率水平的随机变化、负荷模型参数的不确定性等,如果把这些参数的随机性考虑在内,则Kp将不再是一个单一的数的概念,而是成为一个满足一定分布规律的随机变量.针对这一情况,电压稳定概率分析问题就变为计算随机Kp的分布问题,再通过它的分布可以计算出系统电压稳定的概率.
前面的分析已经指出,当Kp>0时系统是静态电压稳定的,因此相应的静态电压稳定概率可以定义为

其中P为概率运算符,ES为电压失稳事件.假设随机变量Kp满足正态分布,其统计特性均值和标准差分别为μKp和σKp,则系统电压静态稳定概率计算公式为

1.2 静态电压稳定的概率分析方法
现有的概率稳定分析方法主要有模拟法和解析法两大类.蒙特卡罗仿真(Monte-Carlo simulation,MCS)法作为模拟法的代表,它能够计及多种随机因素,简单方便,缺点是为了满足一定的精度,需要进行大量的抽样和重复计算[5].与MCS法相比,解析法通常对所研究的概率分析问题进行不同程度的简化,可能出现较大误差.典型的解析法有半不变量法[11]和TPE法[6,10]等.因此,概率稳定性分析的最大难题是计算精度和计算量之间的矛盾.
若随机变量z为随机参数x的函数,理论上可以由 x的分布得到z的分布,但是当两者关系比较复杂时,z的分布的计算将变得极其困难,需要适当的数值计算方法求取.TPE法是一种有效地获取随机变量统计特征的方法,它能够通过较少的运算得到随机变量的统计特征,如均值、方差等.目前TPE法已广泛用于电力系统概率计算中,如随机潮流计算、可用传输容量计算和小扰动概率稳定分析等[6,10].本文利用TPE法进行电压稳定概率分析,假定Kp服从正态分布,把该指标视为电源侧参数、功率水平和负荷模型参数等随机参数的函数,通过TPE法获Kp的统计特征,从而计算得到系统的电压稳定概率.
假设所需求得的随机变量为Kp,可表示为随机向量x的函数如下:

式中:N——随机变量的个数;xk——随机变量.定义xk的第l阶中心矩M及其相对于标准差的系数L如下:
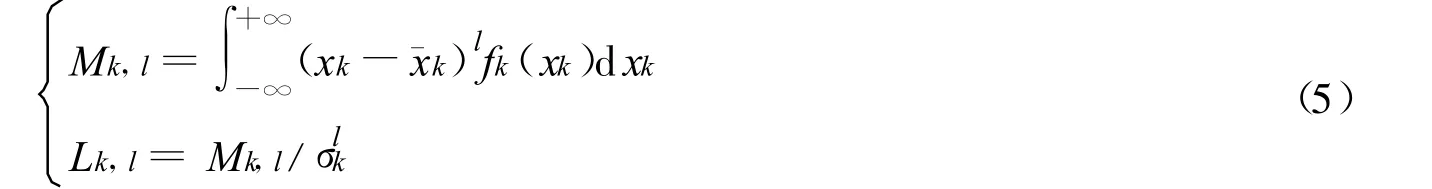
式中,下标l=1,2,……分别表示一阶、二阶到高阶,¯xk,σk,fk分别表示xk的均值、标准差和概率密度函数.则容易得到一阶矩Lk,1=0,二阶矩Lk,2=1,三阶矩Lk,3为xk的斜度系数.Kp的第l(l=1,2)阶矩的估计值、均值和标准差可以按以下公式计算:
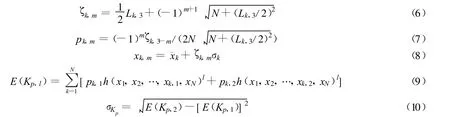
式中:ζk,m,pk,m——位置系数和权重系数;E(Kp,l)——Kp的l阶矩估计值,特别地,当l=1时即为E(Kp),也就是Kp的均值μKp;σKp——Kp的标准差.可以看出,由式(9)和(10)求解Kp的第l(l=1,2)阶矩的估计值和标准差时,实际上完全可以避免建立Kp与随机变量x的复杂函数关系,而通过仿真的方法计算待求Kp的均值和标准差等统计信息.
2 静态电压稳定概率分析的计算步骤
根据上述分析,将Kp表述为电源侧参数、负荷功率水平、负荷模型参数等随机变量的函数,则基于TPE法的静态电压稳定概率分析步骤如下:
a.将静态电压稳定分析中所有需要考虑的随机参数组成一个N维随机向量x,逐个选择x中的随机变量xk,保持x中其他变量为均值不变,由式(5)计算每个随机变量的斜度系数Lk,3(k=1,2,…,N).
b.对每个随机变量xk分别由式(6)和式(7)计算出相应的位置系数ζk,m和权重系数pk,m(m=1,2).
c.依次对每个随机变量xk进行2次确定性静态电压稳定分析,仿真计算得到对应的Kp值,其中变量两点取值为xk,m=¯x+ζk,mσk(m=1,2),通过式(9)和(10)计算出与xk对应的随机变量Kp的第l(l=1,2)阶矩的估计值.
d.全部随机变量循环完毕后,根据式(9)和(10)分别得到Kp的均值μKp、标准差σKp等.
e.由所得的Kp的分布特征(均值和标准差),依据式(3)通过数值积分计算系统在考虑这些随机参数分布下的系统静态电压稳定概率.
从上述计算步骤可以看出,运用TPE法进行静态电压稳定概率分析,实际上无需事先建立Kp与系统中电源侧参数等随机变量的显函数关系,只需在每个随机变量上通过仿真计算2次Kp值,避免了求解高阶偏导数.与MCS法相比,该方法不会因为随机变量维数增加而带来计算量的显著增加,对于一个具有N个随机变量的概率分析只需进行2N次确定性静态电压稳定分析即可获得待求的随机变量Kp概率分布的统计特征及系统的静态电压稳定概率.
3 算例分析
3.1 静态电压稳定概率分析的TPE方法验证
下面以文献[16]中简单2节点电力系统为例,首先对静态电压稳定概率分析的TPE方法(以下简称本文方法)进行仿真验证,然后再与5000次MCS法以及随机参数在其均值¯x处进行确定性静态电压稳定分析(简称均值法)得到的结果进行比较,假设均值法获得的Kp为其均值.验证时假设随机参数为负荷功率水平P0和Q0,分别满足正态分布N~(0.9,0.1)和N~(0.44,0.1),且相互独立,其他参数与文献[16]中第2节分析所用参数一致.表1给出了上述3种方法计算得到的 μKp结果和所需确定仿真计算次数的结果比较,从表1可以看出,使用均值法只能获得假设的 μKp,而无法得到方差等其他统计信息,因此无法保证其精度要求和获得最终的电压稳定概率,而使用MCS法要达到与本文方法相当的精度则要付出比本文方法多得多的Kp相关仿真计算次数,图2则给出了由MCS法和本文方法所得的Kp的累积概率密度函数曲线,2条曲线吻合度很高,证明了本文方法的有效性.

表1 3种方法分析结果比较Table 1 Comparison of results of 3 methods
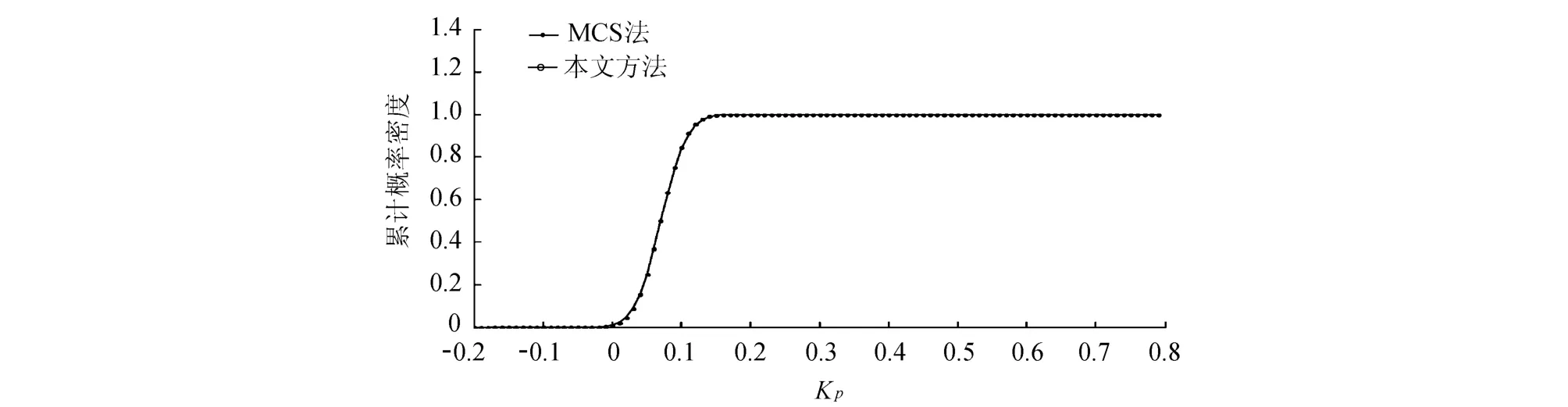
图2 累积概率密度曲线对比Fig.2 Comparison between curves of cumulative density of Monte-Carlo simulation method and two-point estimate method
3.2 随机参数对静态电压稳定概率的影响
上面通过2个随机参数验证了本文方法静态电压稳定概率分析的有效性和快速性,它能够通过较少的计算得到Kp的统计特征从而求得系统的静态电压稳定概率.以下增加所要考虑的随机变量和改变随机参数的统计特征,来研究各随机参数对静态电压稳定概率的影响.假设所有随机变量均相互独立,且均满足正态分布,负荷静态特性中有功和无功的恒阻抗和恒功率的比例参数独立且同分布,表2给出了所有随机变量的统计特征及相应的概率分析结果.
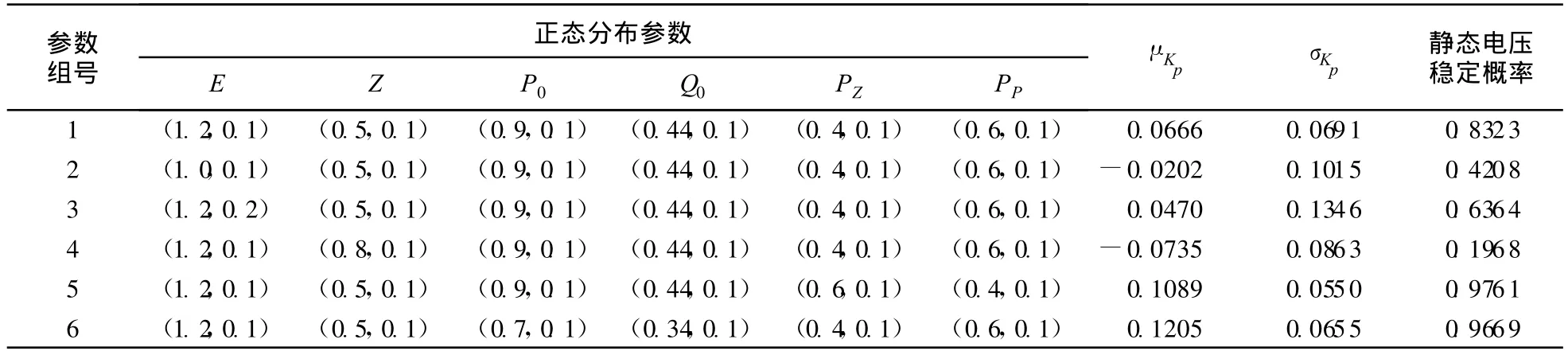
表2 随机变量统计特性及概率分析结果Table 2 Statistical characteristics of random variables and results of probability analysis
首先,将表2中第1组参数分布及概率稳定分析结果,与3.1节中只考虑负荷功率水平随机量的概率稳定分析结果进行比较,不难发现,在其他参数确定时,考虑参数随机因素越多,系统的电压稳定概率会越低.然后比较表2不同参数分布下的概率稳定分析结果,可以得到以下结论:
a.由第1组和第2组参数分布和其概率结果可见,提高电源内电势均值可以有助提高系统的静态电压稳定概率,这与确定性电压稳定分析结果一致.
b.由第1组和第3组参数分布和其概率结果可见,保持电源内电势均值不变时,其标准差越大,系统电压稳定概率越小,这一结论对于其他参数也成立.
c.由第1组和第4组参数分布和其概率结果可见,保持其他随机参数分布不变时,降低电源侧阻抗均值有助于提高系统的静态电压稳定概率.
d.由第1组和第5组参数分布和其概率结果可见,当其他参数分布给定时,负荷静态特性的恒阻抗比例的均值越高,恒功率比例的均值越低,对应的电压稳定概率越大.
e.比较第1组和第6组参数分布和其概率结果可见,负荷功率水平均值越低,对应的系统的电压稳定概率就越大.
这些结论还可以推广到低压减载对静态概率稳定的影响中去.这里作个假设,低压减载后仅负荷的功率水平的均值减小,负荷静态模型参数的其他参数的统计特征未发生明显变化,则显而易见,低压减载可以大大提高系统的静态电压稳定概率.
4 结 论
将TPE法应用于静态电压稳定的概率分析中,利用本文提出的静态电压稳定广义裕度指标功率差裕度Kp进行概率稳定计算,无需建立复杂的函数关系,避免了要像解析法那样对概率问题进行不同程度的简化,只需通过仿真计算的方法获得Kp即可,对于一个具有N个随机参数的系统,只需要进行2N次Kp的仿真计算,即能获得Kp的统计特征,进而求出系统的静态电压稳定概率,这在计算精度和计算速度上得到了很好的折中.算例结果表明,该方法及所提出的静态电压稳定指标是有效的.考虑系统诸多随机因素,如发电侧参数的随机性和负荷侧参数的随机性的仿真算例,表明提高电源内电势,降低电源侧阻抗以及有效的低压减载措施均有助提高系统的静态电压稳定概率,另外负荷静态特性中的恒阻抗及恒功率比例对静态电压稳定影响也同样不可忽视,负荷静态特性的恒阻抗比例的均值越高,恒功率比例的均值越低,对应的系统静态电压稳定概率越大.
[1]BURCHETT R C,HEYDT G T.Probabilistic methods for power system dynamic stability studies[J].IEEE Transactions on Power Apparatus and Systems,1978,97(3):695-702.
[2]鞠平,马大强.电力系统的概率稳定性分析[J].电力系统自动化,1990,14(3):18-23.(JU Ping,MA Da-qiang.Probabilistic analysis of power system stability[J].Automation of Electric Power Systems,1990,14(3):18-23.(in Chinese))
[3]鞠平,吴耕扬,李扬.电力系统概率稳定的基本定理及算法[J].中国电机工程学报,1991,11(6):18-24.(JU ping,WU Genyang,LI Yang.Fundamental theorems on probabilistic stability of power systems[J].Proceedings of the CSEE,1991,11(6):18-24.(in Chinese))
[4]曹一家,程时杰.电力系统静态稳定性的概率分析[J].华中科技大学学报:自然科学版,2005,33(5):75-81.(CAO YI-jia,CHEN Shi-jie.Probabilistic analysis of the steady state stability of power system[J].Journal of Huazhong University of Science& Technology:Nature Science Edition,2005,33(5):75-81.(in Chinese))
[5]李文沅,卢继平.暂态稳定概率评估的蒙特卡罗方法[J].中国电机工程学报,2005,25(10):18-23.(LI Wen-yuan,LU Ji-ping. Montecarlo method for probabilistic transient stability assessment[J].Proceedings of the CSEE,2005,25(10):18-23.(in Chinese))
[6]SU Chun-lien,LU Chan-nan.Two-point estimate method for quantifying transfer capability uncertainty[J].IEEE Trans onPower Systems,2005,20(2):573-579.
[7]HU Zhe-chun,WANG Xi-fang.A probabilistic load flow method considering branch outages[J].IEEETrans on Power Systems,2006,21 (2):507-514.
[8]王克文,钟志勇,谢志棠,等.混合使用中心矩与累加量的电力系统概率特征根分析方法[J].中国电机工程学报,2000,20 (5):37-41.(WANG Ke-wen,ZHONG Zhi-yong,XI Zhi-tang,et al.A hybrid algorithm using moment and cumulant for power system probabilistic eigen value analysis[J].Proceedings of the CSEE,2000,20(5):37-41.(in Chinese))
[9]陈为化,江全元,曹一家,等.电力系统电压崩溃的风险评估[J].电网技术,2005,29(19):6-11.(CHEN Wei-hua,JIANG Quanyuan,CAO Yi-jia,et al.Risk assessment of voltage collapse in power system[J].Power System Technology,2005,29(19):6-11.(in Chinese))
[10]易海琼,程时杰,侯云鹤,等.基于点估计的电力系统小扰动概率稳定分析[J].电力系统自动化,2007,31(23):1-4.(YI Haiqiong,CHENG Shi-jie,HOU Yun-he,et al.An efficient point estimate method for probabilistic small signal stability analysis[J]. Automation of Electric Power Systems,2007,31(23):1-4.(in Chinese))
[11]戴剑锋,王海超,周双喜,等.基于负荷裕度随机特性的电压失稳概率问题研究[J].中国电机工程学报,2006,26(13):26-30.(DAI Jian-feng,WANG Hai-chao,ZHOU Shuang-xi,et al.A study on probability of voltage instability based on the stochastic characteristic of load margin index[J].Proceedings of the CSEE,2006,26(13):26-30.(in Chinese))
[12]周玮,彭昱,孙辉,等.一种用于含风电场电力系统电压稳定概率分析的混合方法[J].继电器,2008,36(2):26-31.(ZHOU Wei,PENG Yu,SUN Hui,et al.A mixed method for voltage stability probabilistic analysis of power systems containing wind energy[J]. RELAY,2008,36(2):26-31.(in Chinese))
[13]吴蓓,张焰,陈闽江.基于负荷模糊聚类的电压稳定概率评估[J].电力系统自动化,2007,31(4):23-27.(WU Bei,ZHANG Yan,CHENG Min-jiang.Probabilistic evaluation of voltage wtability based on load fuzzy clustering[J].Automation of Electric Power Systems,2007,31(4):23-27.(in Chinese))
[14]熊宁,程浩忠,马则良,等.负荷不确定性电网的电压稳定性评价方法[J].电力系统自动化,2008,32(8):24-27.(XIONG Ning,CHEN Hao-zhong,MA Ze-liang,et al.Voltage stability assessmentmethod for power system with load uncertainty[J].Automationof Electric Power Systems,2008,32(8):24-27.(in Chinese))
[15]周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2003.
[16]侯学勇,鞠平,陆扬文.电力系统静态电压稳定的三维分析与临界电压[J].河海大学学报:自然科学版,2008,36(3):396-400.(HOU Xue-yong,JU Ping,LU Yang-wen.Three-dimensional analysis of the static voltage stability and the critical voltage in power system[J].Journal of Hohai University:Nature Science,2008,36(3):396-400.(in Chinese))
