双层球面网壳的风振特性与等效静风荷载
2010-03-14张建胜
吴 迪,武 岳,张建胜
(1.哈尔滨工业大学土木工程学院,哈尔滨150090,forseti2001@163.com; 2.浙江工业大学建筑工程学院,杭州310014)
球面网壳是实际工程中采用较多的一种大跨度空间结构形式,对其抗风设计方法现行规范中尚无明确规定.以往学者研究也多以单层球面网壳的抗风性能为主[1-2],而针对双层球面网壳的较少.从实际工程来看,双层球面网壳的应用更为广泛,因此,有必要通过系统研究提出有针对性的抗风设计方法.针对这种情况,本文以实际工程为背景,结合风洞试验结果对双层球壳结构的风致动力响应特性进行了系统研究,在此基础上提出了一种不同于传统风振系数的等效静风荷载表达方法,可以供设计人员参考.
1 工程及风洞试验简介
1.1 工程介绍
工程背景为浙江某电厂拟建的两座连续排列的球壳煤仓,煤仓屋盖采用双层网壳结构,其下由36根扶壁柱和混凝土墙体共同支撑,球壳跨度(L)125 m,矢高(f)47 m,屋檐高度(h)18 m,建筑面积12 265 m2,其规模在国内是少有的(图1).该结构质量轻、柔性大,属典型的风敏感结构,且建于沿海台风多发地区,风荷载在结构设计中起控制作用,其抗风性能值得深入研究.
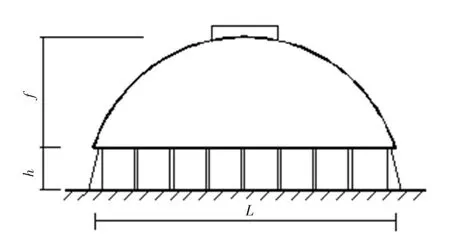
图1 双层球壳结构示意图
1.2 风洞测压试验
风洞试验在航空工业总公司第627研究所的FL9航空风洞中进行.试验基本风速设为12 m/s和18 m/s,参考高度定为模型顶部高度,模拟B类地貌风场.通过在风洞前段设置尖塔、立方体粗糙元和锯齿带作为扰流装置,经过反复调试,使试验段风剖面在两个风速下,均能和理论风剖面相吻合,近地湍流度>10%.试验模型的几何缩尺比为1∶272,满足阻塞度<3%的要求,在风洞中的模型照片见图2.试验中采用多通道测压系统对各测压点进行同步测量,以准确获得屋盖风压间的相关性能[3].

图2 风洞试验模型
1.3 风荷载特性
图3(a),(b)分别给出了由风洞试验获得的平均风压和脉动风压系数等值线.可以看出平均风压总体上表现为风吸力的作用,其分布具有与风的来流相垂直的特性,即在各垂直于来流的截面上风压系数基本接近;最大负压均出现在壳顶帽迎风面两侧.脉动风压受特征湍流的影响,分布规律性较差,其最大值出现在背风侧的再附区内.
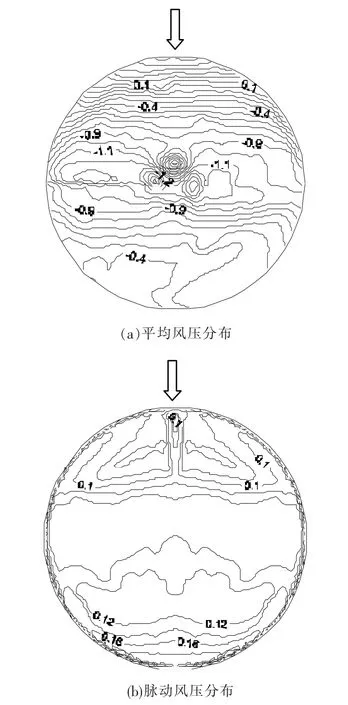
图3 球壳风压系数分布
2 双层球壳的风振特性分析
2.1 计算模型及自振特性分析
计算模型采用角锥型双层球面网壳,几何参数按实际结构选取,边界约束条件为周边三向固定铰接支座.网壳结构的杆件采用2倍安全度选用原则,共1 973个节点、7 664根杆件.结构阻尼比取为0.02,钢管弹性模量E=2.06×108kN/ m2.ANSYS中的有限元模型(图4)均由link8和mass21单元构成.
结构的风振性能不仅与来流的脉动特性有关,还与结构自身的动力特性密切相关.因此,在进行风振分析前,有必要对结构的自振频率和振型作相应地探讨.本文采用子空间迭代法对双层球壳进行了模态分析,图5给出了计算模型的自振频率分布情况,并与一典型单层球壳进行了对比.可以看出两类结构自振频率分布都十分密集,不同点是双层球壳的基频更高,且不存在单层球壳的频率跳跃现象.
图6给出了计算模型的前四阶振型,可以看出第1、2阶振型主要为水平振动,呈反对称分布;第3、4阶振型为水平与竖向的耦合振动.
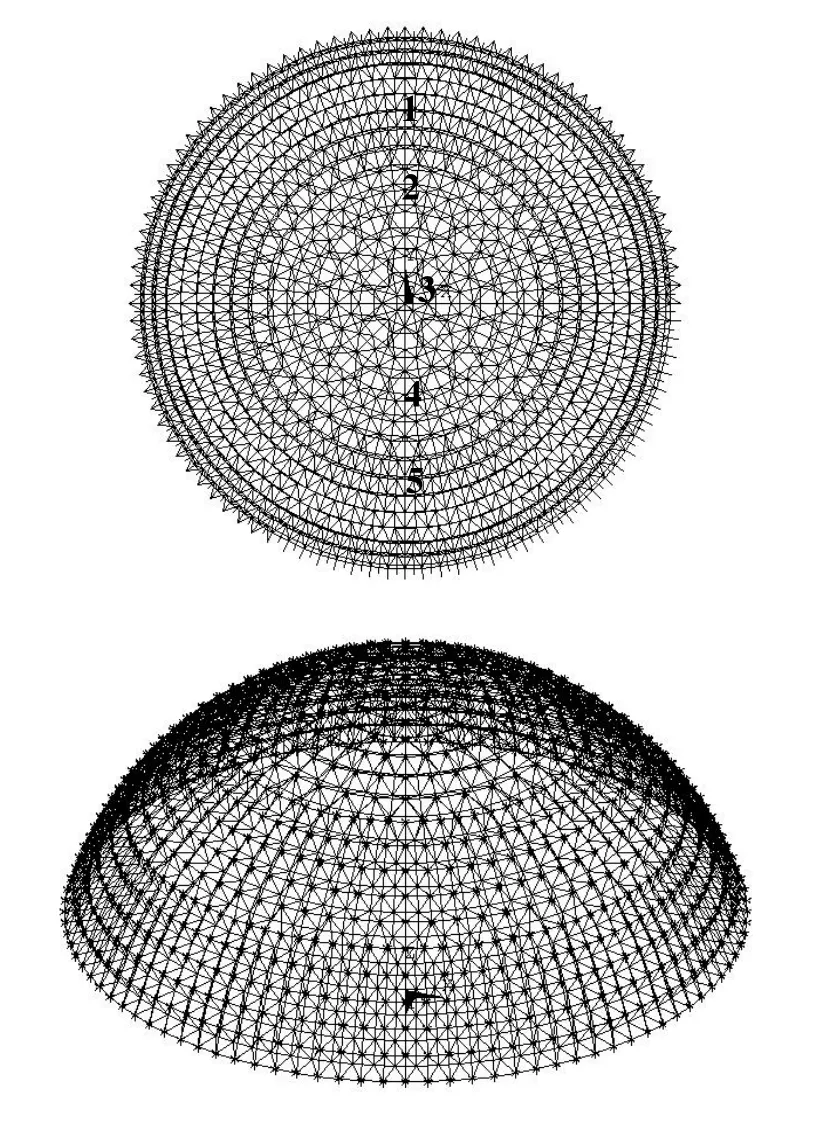
图4 计算模型示意图
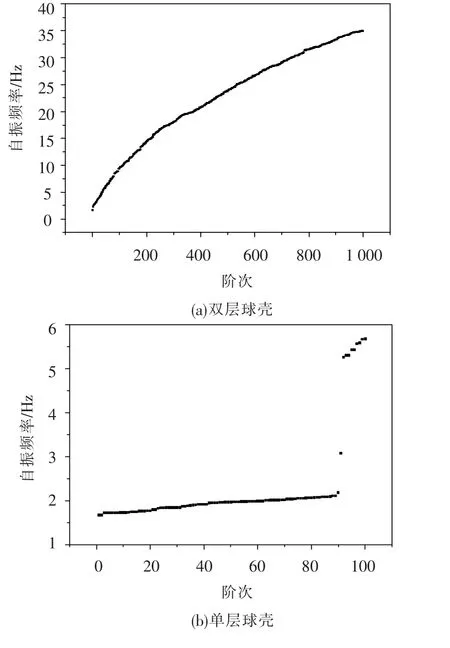
图5 自振频率分布曲线
2.2 风振响应分析
以风洞试验结果为依据,参照文献[4,5]的方法对该结构进行风振响应分析,分别获得结构的背景响应和共振响应及相应的频谱特性.图7给出了典型节点(位置见图4)竖向位移均方根响应,可以看出,跨中结点的位移响应最大,离边界越近,节点位移响应越小.这是由于跨中结点的约束条件较弱,而靠近边界的约束条件较强.

图6 双层球面网壳振型图
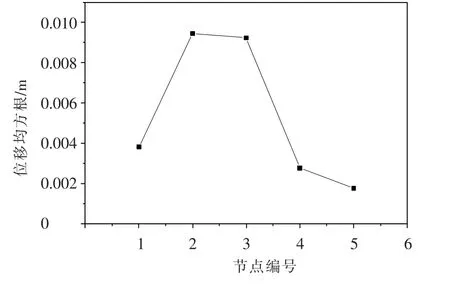
图7 典型节点竖向位移均方根
图8和图9分别给出了部分节点(见图4)的背景和共振响应占总响应的比例及功率谱.可以看出,结构的背景位移响应与共振位移响应明显分离,不同点响应分量占总响应的比例不相同,但总体上看,位移响应的能量主要集中在1.0 Hz以下,说明位移响应以背景响应为主;即对这类刚度较大的双层球壳而言,结构对风荷载的动力放大作用可以忽略不计,而只需考虑脉动风荷载的准静力效应,造成这种现象的原因是这类双层球壳自振频率较高,远离脉动风的卓越频率.
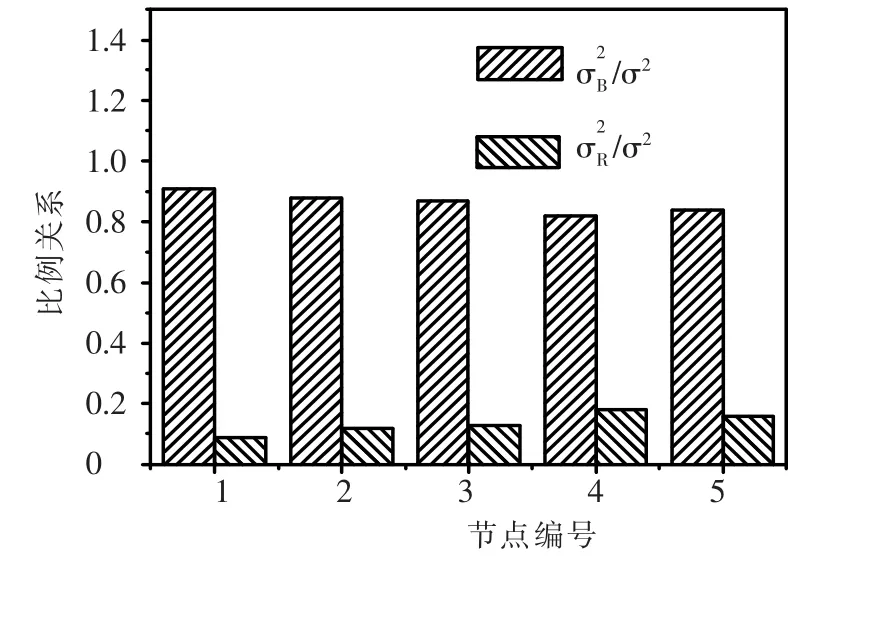
图8 背景和共振响应占总响应的比例
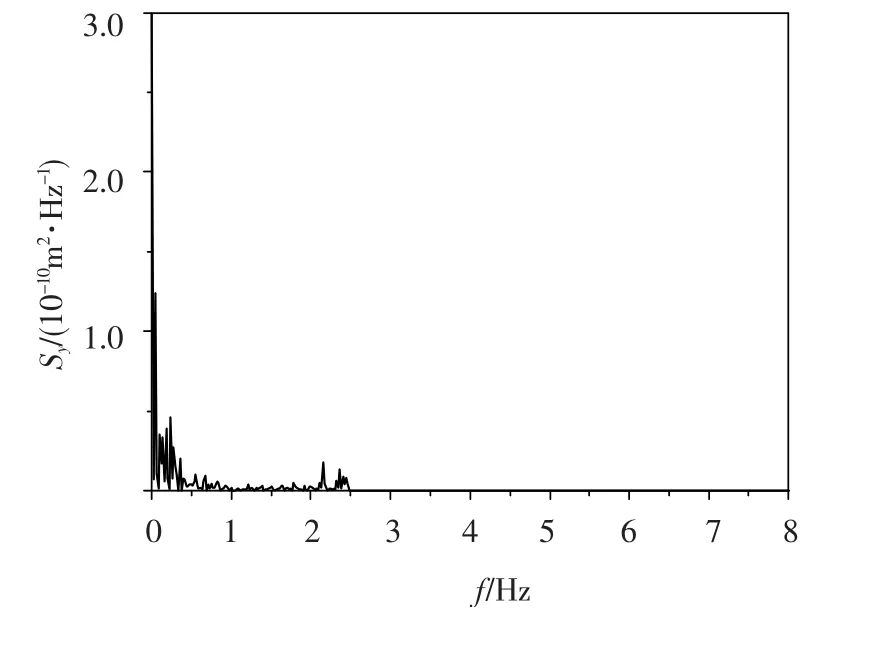
图9 顶点位移响应谱
3 等效静风荷载的确定
3.1 现行规范等效静风荷载确定方法评述
等效静风荷载是联系风工程研究与结构设计的纽带,其作用是将复杂的随机振动问题转化为静力分析问题[6-8],目前各国荷载规范多以风振系数的形式表示等效静风荷载,以我国规范为例,按下式定义荷载风振系数:

式中:^p(z)为等效静风荷载;¯p(z)为平均风荷载; Pd(z)为第一阶振型惯性力的幅值;g为峰值因子;σ1为第一阶振型的均方根响应.
可以看出,式(1)以结构第一阶振型惯性力作为等效静风荷载,对于高层和高耸建筑等第一阶振型占主导地位的结构无疑是合适的,但对于双层球壳等大跨度屋盖结构,由于结构风振响应常常呈现多振型共同参与的特点,其等效静风荷载的确定需要考虑多阶惯性力的作用.针对这一问题,有学者提出了考虑多振型参振的精细化等效静风荷载分析方法[9],但其计算比较繁琐,难以为设计人员掌握,亟需提出实用化的等效静风荷载分析方法.另外,从表达方式上看,传统风振系数以平均风荷载作为等效静风荷载的基向量,当平均风荷载很小时,风振系数将非常大.实际应用中这种方法往往导致支座附近节点风振系数较大,不能合理地反映结构风振特性.为解决上述问题,本文从风荷载作用机理和双层球壳结构的自身特性出发,提出一种面向工程应用的等效静风荷载简化表达方法,其基本思路是选择脉动风荷载均方差{σF}作为等效静风荷载的基向量.
3.2 本文等效静风荷载确定方法
基于第三节的分析,可以认为双层球壳的等效静风荷载可忽略共振分量,仅考虑平均分量和背景分量,其表达式如下:
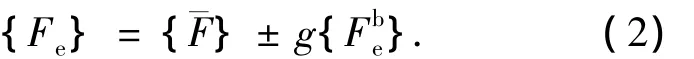
式中:{Fe}为总等效静风荷载为平均风荷载为等效静风荷载背景分量;g为峰值因子.
由结构背景响应的定义可知其本质上反映的是脉动风荷载的准静力效应,据此选择脉动风荷载均方差{σF}作为等效静风荷载背景分量的基向量,采用线性代数方法确定基向量的最优系数,使得到的等效静风荷载同时适用于多个等效目标.等效静风荷载背景分量的表达形式如下:

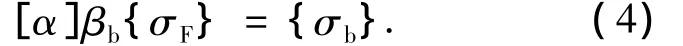
式(4)相当于一个以βb为未知数的非齐次线性方程组,由线性代数知识可知,对于单一等效目标,βb的解是唯一的;等效目标多于一个时,方程不存在精确解,此时只能得到最小二乘意义上的解.
可以看出,本文方法与传统风振系数法的最大区别是基向量的选取,本文选择脉动风荷载均方差作为等效静风荷载的基向量无疑更符合风荷载作用机理.同时,采用本文方法只需进行一次计算就可以获得针对多个等效目标的等效静风荷载,十分有利于工程设计.
利用上文提出的方法对本文的双层球壳进行分析,以节点竖向位移为等效目标,确定 βb为0.96,据此得到等效静风荷载分布如图10所示,其中等效静风荷载以风压系数表示,参考点为球壳顶部高度.在该荷载的静力作用下,各等效目标响应与实际动力响应{^y}的对比如图11所示,可以看出,等效静风荷载分布规律较好,且在该等效静风荷载作用下的位移响应与实际动力响应极值总体上吻合较好,验证了本文方法的有效性.需要说明的是,对于其他类型响应(如杆件内力、支座反力等),应用本文方法同样可以得到较好的效果,限于篇幅不再赘述.

图10 总等效静风荷载
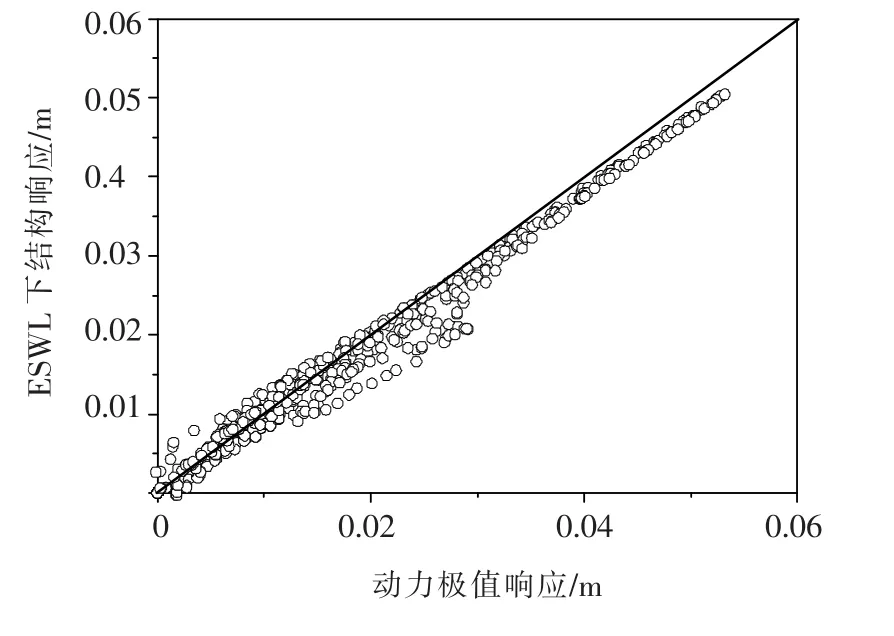
图11 等效静风荷载下的位移响应
4 结论
1)以实际工程为例,对双层球壳结构的风振特性开展了系统研究,结果表明,对于这类刚度较大的双层球壳,脉动风响应以背景响应为主,结构对风荷载的动力放大作用可以忽略不计.
2)针对双层球壳结构的风振特性,以脉动风荷载均方差作为等效静风荷载背景分量的基向量,提出了一种不同于传统风振系数的等效静风荷载表达方法,并将其应用于本文的双层球壳中,证明了本文方法的准确性和有效性.
[1]NAKAYAMA M,SASAKI Y,MASUDA K,et al.An efficient method for selection of vibration modes contributory to wind response on dome-like roofs[J].Journal of Wind Engineering and IndustrialAerodynamics,1998,73:31-43.
[2]黄明开,倪振华,谢壮宁.大跨圆拱屋盖结构的风振响应分析[J].振动工程学报,2004,17(3):275-279.
[3]黄鹏,全涌,顾明.TJ-2风洞大气边界层被动模拟方法的研究[J].同济大学学报,1999,27(2):136 -141.
[4]陈波,武岳,沈世钊.大跨度屋盖结构等效静力风荷载背景分量的确定方法探讨[J].工程力学,2006,23(11):21-27.
[5]陈波,武岳,沈世钊.大跨度屋盖结构等效静力风荷载中共振分量的确定方法研究[J].工程力学,2007,24(1):51-55.
[6]武岳,陈波,沈世钊.大跨度屋盖结构等效静风荷载研究[J].建筑科学与工程学报,2005,22(4):24-31.
[7]KASPERSKI M,NIEMANN H J.The LRC(load-response correlation)method:A general method of estimating unfavorable wind load distributions for linear and nonlinear structural behavior[J].Journal of Wind Engineering and Industrial Aerodynamics,1992,43:1753-1763.
[8]KASUMURA A,TAMURA Y,NAKAMURA O.Univesal wind load distribution simultaneously reproducing largest load effects in all subject members on large span cantilevered roof[J].Journal of Wind Engineering and Industrial Aerodynamics,2007,95:1145-1165.
[9]HOLMES J D.Effective static load distributions in wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90:91-109.
