单层球面网壳与支承结构整体强震失效特征
2010-03-14于志伟支旭东沈世钊
于志伟,支旭东,范 峰,沈世钊
(哈尔滨工业大学土木工程学院,哈尔滨150090,cefish2008@163.com)
目前,网壳结构在地震等动力作用下的研究主要包括:动力特性、弹塑性地震响应、动力稳定性、强震下的失效模式及失效机理[1-5].随着对网壳结构强震作用下失效机理研究的深入,考察网壳结构强震作用下构件以及结构的塑性发展能力,明确结构的破坏模式、破坏机理及其与各种因素之间的关系,提出合理的破坏准则和有效的抗震设计方法等问题[6-9],成为继网壳动力稳定问题之后研究的热点.然而,对网壳结构在强震作用下的研究工作都是基于简化的分析模型,即把下部的支承体系与上部的网壳结构分开考虑,以简支或固支边界来模拟网壳的支承情况,进行独立的力学性能计算.但考虑到使用功能,一般将钢网壳屋盖支承在混凝土框架或混凝土柱子上.若不考虑下部支承结构对网壳结构动力性能的影响,将会与实际情况产生较大偏差.
本文建立了更为精细化的数值模型,采用动力荷载域全过程分析方法,对单层球面网壳与支承结构整体在强震作用下的特征响应进行分析,研究了下部支承结构对单层球面网壳在强震作用下失效特征的影响,并对单层球面网壳进行大规模的参数分析,阐述了下部支承结构、矢跨比、屋面质量等参数对网壳结构在强震作用下动力响应的影响,得到了单层球面网壳与支承结构整体在强震作用下的失效规律.
1 模型及参数选取
采用Kiewitt8(K8)型单层球面网壳作为上部网壳结构.下部支承结构采用柱子-环梁体系,柱脚固结与地面,上部网壳支座节点铰接于环梁上,如图1所示.采用大型有限元分析软件ABAQUS.文中将整体模型以代号表示,符号概念如图2所示.

图1 网壳整体结构图

图2 整体结构代号图
1.1 网壳结构模型
以跨度为40 m的K8型单层球面网壳为研究对象,矢跨比分别为1/3,1/5和1/7,屋面质量分别为0.6,1.2和1.8 kN/m2,采取质量凝聚的方法,按结构静力稳定控制,以安全系数法选择截面,安全系数取为2.0.杆件截面的选择,不考虑下部支承结构的影响.
在强震下的网壳结构内部经常产生比较明显的材料塑性损伤,为考察这种损伤累积对结构性能的影响,根据工字型截面构件的空间滞回试验[10]所获得的考虑材料损伤累积的本构关系,编制了基于ABAQUS的用户材料子程序,对网壳结构在强震下的响应进行研究.在研究中发现,考虑材料损伤累积可能对网壳结构的力学行为产生较为明显的影响,特别是结构的极限承载力,影响最大可达20%.在计算中应考虑材料损伤累积的弹塑性本构模型,同时考虑几何非线性和材料非线性的影响.材料屈服强度fy=235 MPa,弹性模量E=2.06e11,材料密度7 850 kg/m3.
1.2 支承结构模型
下部支承结构(目前仅对网壳结构的失效特征加以研究,并未考虑支承结构的破坏),采用的是柱子-环梁体系,为了理论研究的方便以及考虑支承结构影响的全面性,将柱子和环梁的截面设置为相同的正方形截面,并取截面尺寸分别为: 0.3,0.6,0.9和1.5 m.在计算中应用理想弹性的本构模型.材料的弹性模量E=3.0e10,泊松比为0.3,材料密度2 500 kg/m3.
1.3 整体模型阻尼比
本文采用钢结构和混凝土结构组合成的组合体系,由于不同材料其能量耗散机理不同,不能简单地取用某一材料的阻尼比作为整体结构的阻尼比.Akenori Shibata[11]提出等效结构法的思路,即含有梁元和杆元的不同材料组合结构的阻尼比实用计算方法——位能加权平均法.
首先分别求出结构中钢构件、钢筋混凝土构件的位能,再与其各自的阻尼比值相乘后加权平均而得出的,即
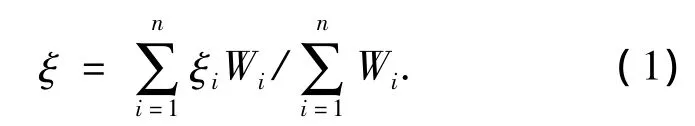
式中:ξ为整体结构阻尼比;ξi为第i个构件阻尼比,对钢结构取0.02,对混凝土结构取0.05;Wi为第i个构件的位能.其中,梁元位能为
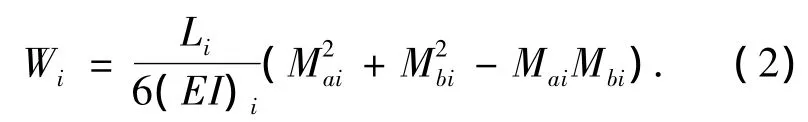
式中:Mai,Mbi为作用在第i个梁元两端的外力偶矩;Li为第i个梁元长度;E为弹性模量;I为单元转动惯量.
整体结构的临界阻尼比确定后,再按式(3)计算结构的Rayleigh阻尼系数
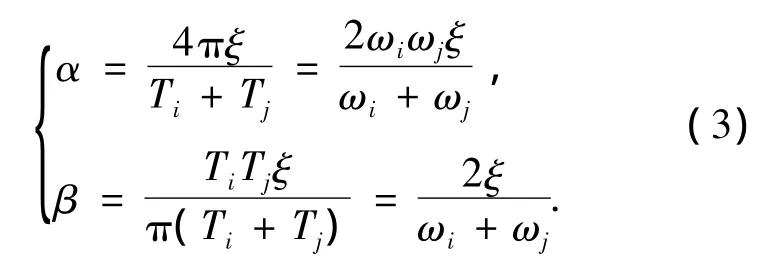
式中:ξ为整体结构的阻尼比;Ti,Tj为整体结构的第i,j个周期;ωi,ωj为整体结构的第i,j个圆频率.
通过位能加权平均法计算得到本文所有算例的整体模型阻尼比均在0.025~0.035,更接近于钢结构的阻尼比0.02,计算结果偏于安全.
2 动力荷载域全过程分析方法
动力荷载域全过程分析方法是一种基于响应的分析方法,即针对不断增大的荷载强度,用有限元方法求解结构在荷载时程范围内的宏、微观响应,并记录这些特征响应;对结构在相应荷载下的表现进行评价,可以判断结构受力性质变化的时刻,以及最终失效倒塌时刻等重要结构特性.采用以下几项特征响应:
1)网壳最大节点位移:宏观上体现了结构的刚度水平;
2)不同屈服杆件比例:结构中出现不同截面屈服程度的杆件比例,按照截面屈服程度不同定义为1P、3P、5P和8P,1P表示杆件截面上8个积分点中至少一个材料进入塑性,余类推,因此8P表示杆件全截面进入塑性,如图3所示;

图3 Beam31单元截面塑性发展定义
3)节点位移时程曲线:判别节点振动是否平衡或结构已振动发散.
3 整体结构失效特征
不考虑支承结构的网壳在强震下的破坏存在两种截然不同的破坏模式,即动力失稳破坏和动力强度破坏.相同的网壳,考虑支承结构会对网壳的强震下的失效特征及失效模式有明显的影响.并且不同刚度支承结构的网壳,对其失效特征的影响也不同.
对于强支承网壳结构,以单层球面网壳D430615为例,其等效临界阻尼为0.025.外圈杆件较早的进入了塑性,由于支承结构刚度较大,对整个网壳有很强的约束作用,对网壳保持有效的抵抗外荷载的整体刚度很有帮助.随着荷载幅值的增大,网壳的塑性发展逐步深入,直到整个网壳均到达很深的塑性.如图4(a)所示,图中进入塑性的杆件用圆圈标注,圆圈越大表示此杆件的塑性应变越大,圆圈中数字表示截面进入塑性积分点数.强支承网壳的失效过程呈现出明显的强度破坏特征,塑性发展全面,可以认为是一种整体的动力强度破坏,本文中所有强支承结构的算例均表现出如上所述的失效特征.
对于弱支承网壳结构,以单层球面网壳D450603为例,其等效临界阻尼为0.035.同样是外圈杆件较早的进入塑性,由于支承结构刚度较小,随着荷载幅值的增大,外圈杆件进入深度的塑性,而网壳的上部杆件并未有塑性分布,此时网壳不能维持整体刚度.局部的外圈杆件失效,导致网壳刚度弱化.网壳失效时上部杆件塑性发展很浅,如图4(b)所示.这种失效但与强支承网壳结构的强度破坏明显不同,是由于局部杆件的失效而引起的,可以认为是一种局部强度破坏.产生这种变形趋势的原因是由于存在下部支承结构,受到的约束作用相对于支座铰接的情况较弱,网壳的外圈杆件受到不利影响,为薄弱部位.同时,本文考虑了环梁对网壳结构失效特征的影响,尤其是弱支承柱加刚性环梁的情况.当保持弱支承柱截面不变,梁的截面从小到大变化时,网壳结构的失效由局部强度破坏趋向于整体强度破坏,网壳结构的塑性发展也越来越深入.
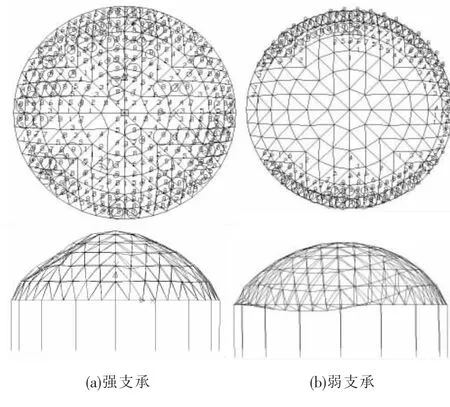
图4 强、弱支承网壳整体失效时刻的特征响应
4 整体结构失效规律研究
针对单层球面网壳与支承整体结构,综合考虑多项参数影响,研究在强震作用下的失效规律.通过大量算例的统计分析,阐述网壳失效时刻的响应规律及失效特征,研究各参数对单层球面网壳与支承整体结构抗震性能的影响.
4.1 极限荷载分析
网壳结构的失效判别方法如下:在网壳动力全过程响应分析中,定义对应多项特征响应指标突然明显变化,结构性质急剧弱化的荷载强度作为结构在此荷载下的失效荷载强度,也称为失效临界荷载.下面以单层球面网壳(D470609)在三维输入TAFT地震作用为例说明极限荷载的确定过程.图5为该算例的结构响应全过程曲线.
荷载幅值-节点最大位移曲线有明显的转折点.随荷载幅值增加,节点最大位移也随之增大.在1 300 gal左右时,曲线出现转折,斜率明显变小,表明结构在1 300 gal荷载幅值下,刚度出现明显弱化,对应的荷载强度增量引起的位移增量显著增大,结构保持平稳的振动而不发生振动发散;当荷载幅值达到1 500 gal,1P比例达100%,8P比例达96%,结构整体杆件塑性发展极为深入.从图5(b)中可以看出,在1 300 gal荷载幅值下,结构的位移相对稳定;在1 500 gal时,最大位移节点的位移时程曲线明显突变,振动发散.综合判定结构的极限荷载幅值为1 300 gal.以下参数分析中的网壳极限承载力均按此方法判别.

图5 特征响应曲线和图形
4.2 整体结构失效规律
对考虑下部支承结构的单层球面网壳在TAFT(1952)地震作用下进行动力响应分析,考察不同结构及荷载参数的变化对网壳结构的失效和抗震性能产生的影响.通过改变下部支承结构、矢跨比和屋面质量分析强震作用下结构的各项响应指标的变化规律.
4.2.1 支承结构的影响
图6为40 m跨度,1/5矢跨比的网壳结构在0.6,1.2和1.8 kN/m2屋面荷载下不同下部支承结构对网壳特征响应的影响.

图6 随支承结构变化网壳失效时刻特征响应
网壳的各项特征响应对网壳下部支承结构的变化非常敏感.当下部支承结构刚度大时,由于对网壳的较好的约束作用,结构的极限承载力很高,塑性深度和广度都较好,延性好.当下部支承结构刚度很弱时,由于较好的减震作用,结构的极限承载力也很好.而对于实际工程中常用的中等刚度的下部支承结构,由于约束作用和减震作用都较弱,网壳的极限承载力较以上两种情况低.
4.2.2 矢跨比的影响
图7为40 m跨度,不同下部结构的单层球面网壳在1.2 kN/m2的屋面荷载下特征响应随矢跨比的变化规律.
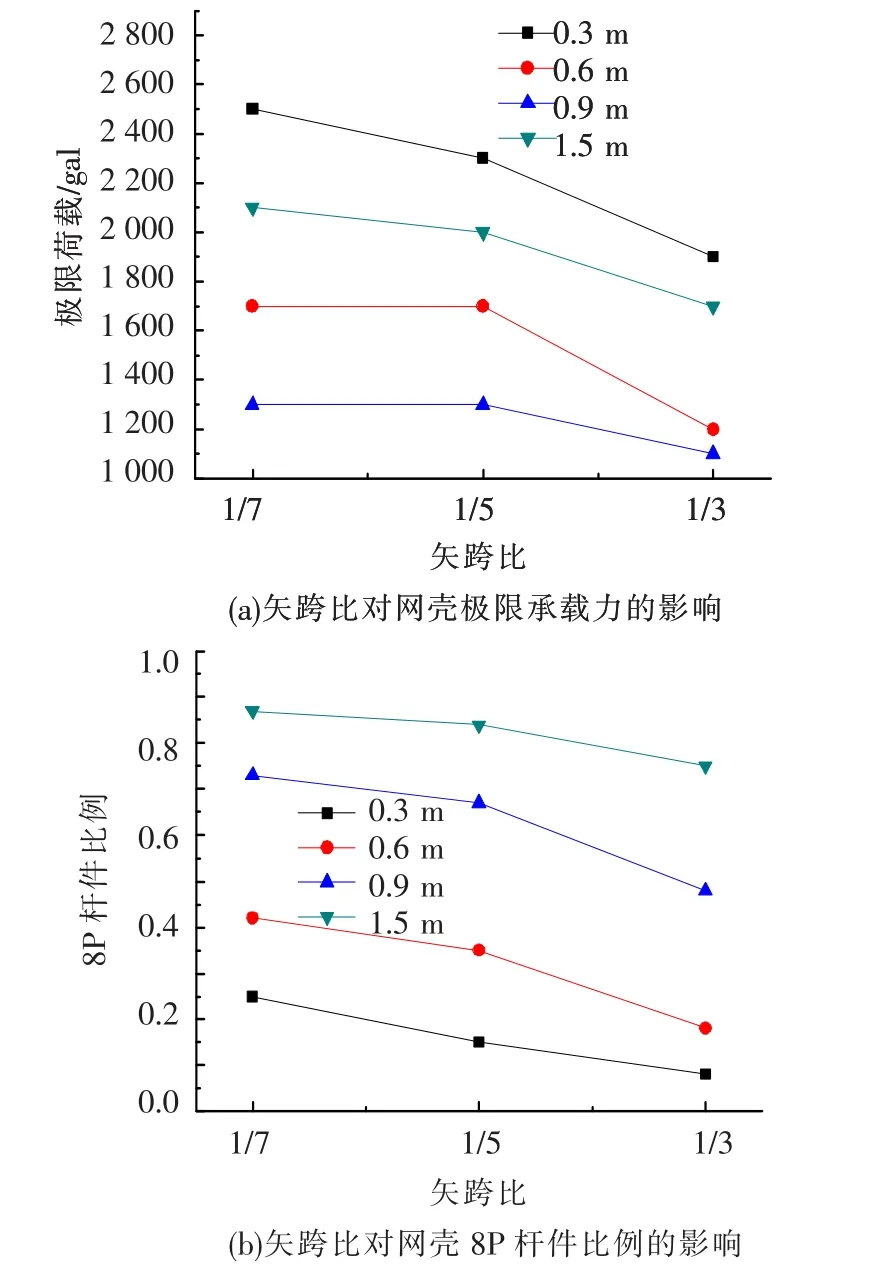
图7 随矢跨比变化网壳失效时刻特征响应
随着矢跨比减小,极限荷载增加.高矢跨比网壳更接近壳体的受力状态,竖向抗震性能较好,抵抗水平荷载的能力较弱,而地震以水平地震为主.因此,失效荷载随矢跨比的增大而降低网壳杆件塑性发展程度随矢跨比的减小而逐渐加深,小矢跨比网壳在失效时上部杆件有大部分进入较深的塑性,随矢跨比的降低结构塑性分布的广度和深度都有提高,表明材料利用率高,结构延性更好.
4.2.3 屋面荷载的影响
图8给出了40 m跨度,矢跨比1/3、1/5和1/7的网壳与支承整体结构在taft地震波作用下的特征响应对比,可以看出屋面质量越大,网壳在地震作用下越不利,网壳的极限承载力越低.
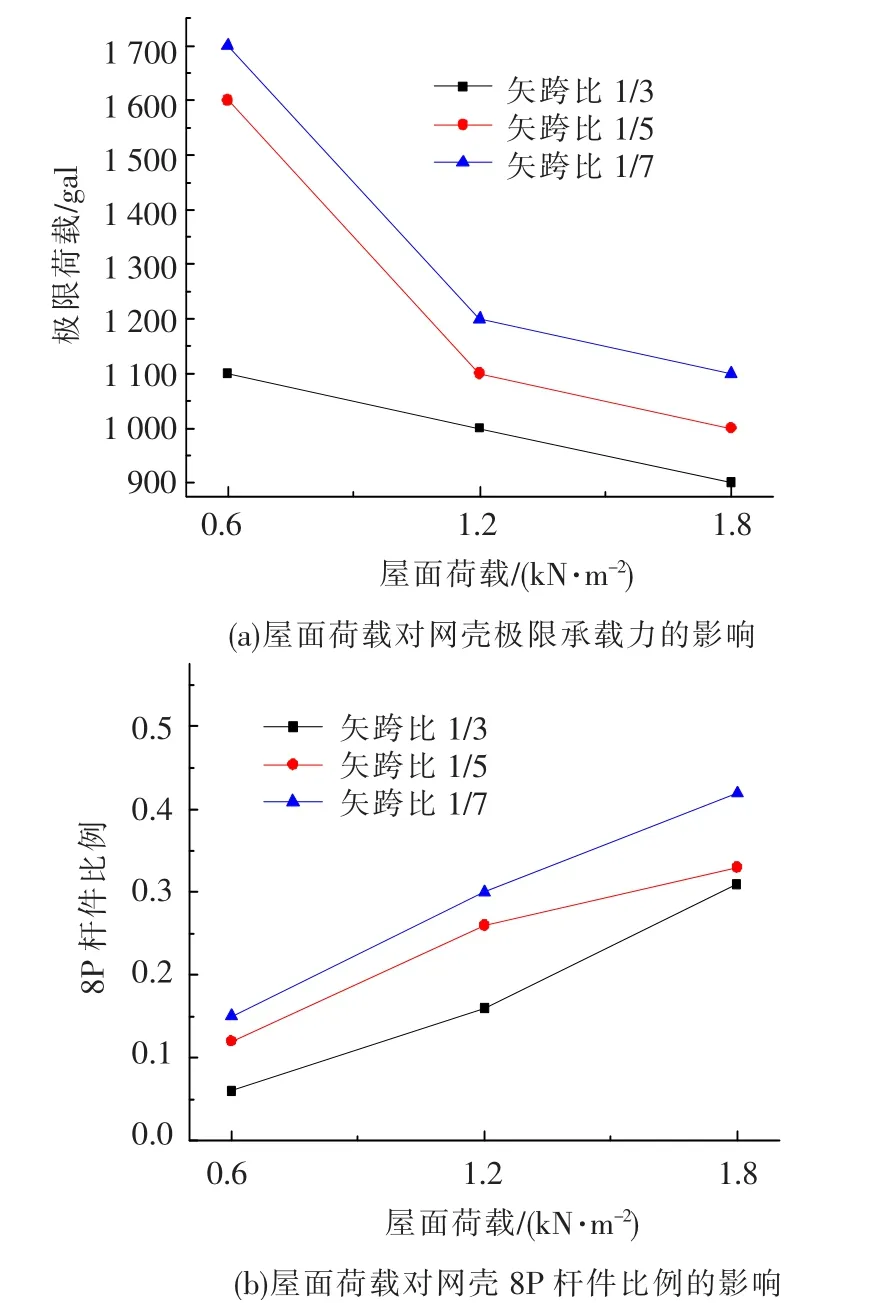
图8 随屋面荷载变化网壳失效时刻特征响应
5 结论
1)在强震作用下,考虑下部支承结构的单层球面网壳,根据下部支承结构刚度不同,存在强支承网壳和弱支承网壳两类不同的失效特征.
2)通过算例分析,得到了失效特征的变化规律:支承结构的影响:网壳的各项特征响应对支承结构非常敏感.当支承结构刚度大时,对网壳的较好的约束作用,结构的极限承载力很高,塑性深度和广度都较好,延性好.当支承结构刚度较弱时,由于较好的减震作用,结构的极限承载力也很好;矢跨比的影响:随矢跨比减小,结构的极限承载力显著提高,并且塑性程度加深,延性增强;屋面荷载的影响:屋面荷载越大,网壳的极限承载力越低.
[1]MOKOWSKI Z S.Space structures-a review of the developments within the last decade[C]//The fourth international conference on space structures.Guildford,UK:University of Surrey,1993:1-8.
[2]SHEN Shizhao.Recent advances on the fundamental research of spatial structures in China[J].Journal of the International Association for Shell and Spatial Structures,2006,47(2):93-100.
[3]BORRI C,SPINELLI P.Buckling and post-buckling behavior of single layer reticulated shells affected by random imperfections[J].Computers&Structures,1988,30:937-943.
[4]FORMAN S E,HUTCHINSON J W.Buckling of reticulated shell structures[J].International Journal of Solids and Structures,1970,6:909-932.
[5]KATO S,UEKI T,MUKAIYAMA Y.Study of dynamic collapse of single layer reticular dome subjected to earthquake motion and the estimation of statically equivalent seismic forces[J].International Journal of Space Structures,1997,12(3-4):191-204.
[6]WANG Bingbing,LI Yingyue.A theoretical study of super-span latticed shells[J].Journal of Constructional Steel Research,1999,51:287-296.
[7]范峰,钱宏亮,邢佶慧.强震作用下球面网壳动力强度破坏研究[J].哈尔滨工业大学学报,2004,36 (6):722-725.
[8]邢佶慧,柳旭东,范峰.单层柱面网壳结构地震模拟振动台试验研究[J].建筑结构学报,2004,25(6): 1-8.
[9]ZHI Xudong,FAN Feng,SHEN Shizhao.Failure mechanisms of single layer reticulated domes subjected to earthquake[J].Journal of the International Association for Shell and Spatial Structures,2007,48(1):29-44.
[10]支旭东,范峰,沈世钊.材料损伤累积在网壳强震失效研究中的应用[J].哈尔滨工业大学学报.2008,40(2):169-173.
[11]SHIBATA A S.Substitute structure method for seismic in design in R.C.[J].Proc ASCE,1976,5:102.
