考虑地面运动的多模态静力弹塑性分析方法
2010-03-14吕西林
张 松,吕西林
(1.同济大学土木工程防灾国家重点实验室,上海200092,zhangsongyy@163.com; 2.中国中元国际工程公司,北京100089)
结构设计的本质就是使结构的能力大于结构的需求,满足提出的各种功能要求,弹塑性动力时程分析方法被认为在理论上是最为完善和精确的计算地震需求的方法,但其计算量大、复杂,限制了其应用,而非线性静力计算方法作为一种结构非线性响应的简化计算方法,得到了广泛的应用[1-2].传统的静力弹塑性分析方法采用不变的加载模式进行推覆分析,这种方法虽然简单但有不可忽视的缺点[3].Gupta和Kunnath指出:尽管大多数结构的第一层层高较大,但最大层间位移并未发生在第一层;在不同时刻惯性力的分布有很大的不同,且高振型的贡献明显;对于大多数的框架结构,在最大层间位移时刻的惯性力分布类似或接近于第二振型的形状[4].Goel和Chopra指出虽然高阶模态的能力曲线在实际工程中很少出现翻转的异常情况,但确实存在,通过考察不同参数的人工地震波作用下一实际结构塑性铰的发展机制,发现破坏形式有可能由第二或第三振型控制[5].Hernandez-montes等提出基于能量的方法解决高阶振型能力曲线异常的问题,易伟建等也采用这一方法改进了pushover分析方法[6-7].一些学者提出了改进的静力计算方法,通过采用弹性振型组合的方式考虑高阶振型的影响[2,8-11].一些学者考虑了结构振动特性的变化,即自适应静力弹塑性分析方法[4,12-13].文献[14-15]都指出了传统的静力弹塑性分析方法不能正确评估结构在近场地震作用下的抗震性能.本文提出了考虑地面运动建立等效单自由度的多模态静力弹塑性分析方法,克服了多模态静力弹塑性分析方法(MPA)在计算等效单自由度时不能考虑地面运动及加载制度仅由结构特性决定的缺点.
1 改进的多模态静力弹塑性分析方法的提出
多模态静力弹塑性分析方法(MPA)的物理意义明确,其基本假设为:1)忽略结构屈服后各模态坐标之间的耦合;2)结构的地震需求值通过各模态SRSS方法得到.对于非线性体系两点假设都不是严格成立的,本文即针对假设的第一点进行研究,在建立等效单自由度时考虑地面运动的影响,提出一种新的等效单自由度的计算方法.最后通过对12层钢筋混凝土标准框架振动台模型为算例进行了对比计算[16].
1.1 改进的建立等效单自由度模式的提出
静力弹塑性分析方法的核心即为采用逐步加载的静力方式给出结构等效单自由度的能力曲线,而影响能力曲线的主要因素则是结构塑性铰的发展机制.传统的多模态静力弹塑性分析方法就是根据多自由度结构的弹性刚度求解结构的前n阶动力参数,用弹性阶段的模态定义加载制度,进行pushover分析,则此时结构非线性行为的发展和地面运动没有关系,完全决定于结构特性,因此也不可能捕捉到结构在地面运动作用下的真实屈服机制.为了在多模态静力弹塑性分析方法中,尽可能捕捉结构真实的非线性行为,首先用弹性阶段的多模态静力弹塑性分析方法计算结构的地震响应,然后再利用计算结果的结构特性定义加载制度,进行pushover分析.以结构非线性行为发展后的结构特性计算,可减少模态坐标之间的耦合程度,从而减少误差.这样在计算等效单自由度时既能考虑地面运动的影响,克服了传统多模态静力弹塑性分析方法的缺点,又避免了自适应多模态静力弹塑性分析方法每步进行振型组合的缺点,且概念简单,理论意义明确.
1.2 改进的多模态静力弹塑性分析方法的步骤
1)基本步骤.a)计算结构弹性状态的结构动力特性(模态、自振周期);b)对第n阶模态计算加载向量;c)对第n阶模态进行推覆计算,并采用位移控制法,建立基底剪力-顶点位移的能力曲线;d)根据n阶模态能力曲线建立n阶等效单自由度;e)用时程分析法计算等效单自由度体系的地震响应,得到各个等效单自由度的峰值响应,再对计算的模态峰值响应(如前三阶模态)进行振型组合(可采用SRSS方法进行组合)得到结构的地震峰值响应;f)根据第e步的结果,重新计算结构的动力特性(模态、周期),此时如果e步计算的峰值响应在结构的弹性范围内,则无需进行计算,e步结果即为最后结果,如结构进入非线性,产生损伤,则计算结构产生损伤后的动力特性; g)重复b~e步,最后得到结构的地震响应.
2)等效单自由度反应量的求解.目前等效单自由度的求解方法有很多,例如周定松,吕西林提出的延性需求谱法[1];Erol Kalkan等提出的等延性能力谱法[13];徐福江,钱稼茹提出用到的常延性系数弹塑性位移谱法[17]等.由于现在的非线性反应谱法还不成熟,能力谱法又缺乏严格的理论基础,为了避免在求解等效单自由度动力反应时产生的误差,在本文中对等效单自由度的地震响应均采用MATLAB语言编程,直接用动力时程法求解,便于分析误差产生的原因.由文献[17]和文献[18]可知滞回模型的刚度和强度退化特性对结构的位移影响较小,为了方便起见,采用双折线模型进行结构的分析,图1为标准框架振动台模型在kobe波作用下通过本文方法得出的等效单自由度双折线模型.
2 分析方法的验证与对比分析
对12层标准钢筋混凝土框架模型建立数值模型(采用CANNY程序),由此确定结构X向前三阶频率分别为4.17,12.42,20.42,与试验中白噪声初次扫描得到的前三阶频率3.74,14.82,28.03基本一致.表1为标准框架振动台试验的动力相似关系,表2为原型结构和模型结构的对比,图2为试验中得到的一个工况顶层X向位移时程图.
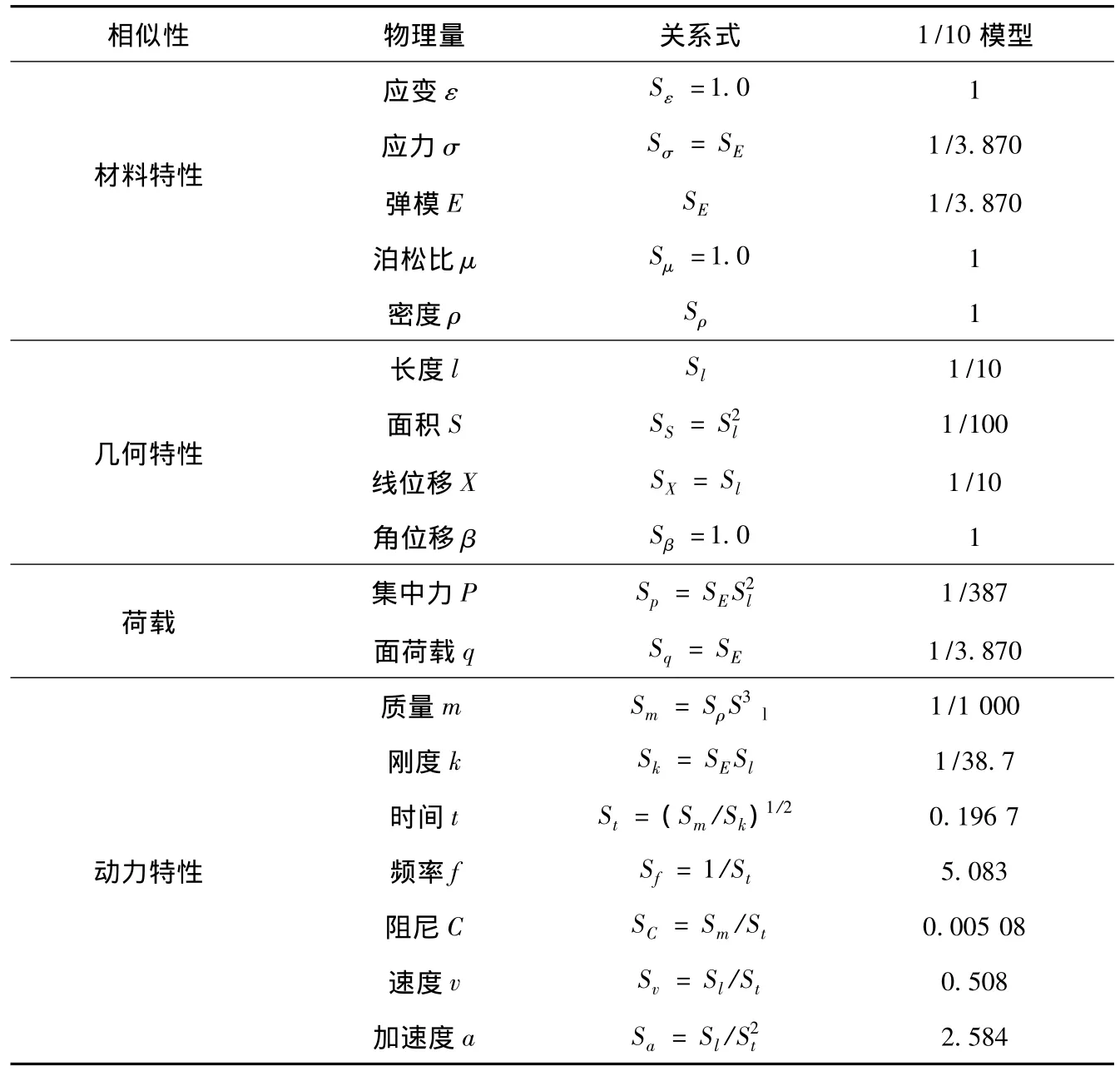
表1 试验模型的动力相似关系

表2 原型和模型对比

图1 等效单自由度的双折线模型(Kobe波)
2.1 模态坐标耦合程度的影响因素
多模态静力弹塑性分析方法,采用结构初始模态坐标进行结构地震响应计算过程中的解耦,并忽略非线性行为发生后各个振型坐标之间的耦合.振型坐标之间的耦合程度和结构以及地面运动相关,结构非线性行为发展越严重,地面运动对高阶振型的激励越明显,则耦合程度越大.
图3和表3为标准框架模型分别在加速度峰值为353.2,775.2 cm/s2和1317.8 cm/s2的Kobe波作用下结构相对地面位移和层间位移的弹塑性动力时程计算方法和多模态静力弹塑性计算方法的计算结果对比,由图3和表3可看出多模态静力弹塑性计算方法的计算结果相对于弹塑性动力时程计算结果的误差并没有随着地震动峰值的增加而增加,分析其原因为结构模型是一个规则的模型,自振特性以第一振型为主,且地震动对高阶振型不敏感,第一阶振型的反应为地震响应量的主要成分.表4为前三阶等效单自由度的顶点位移,由表中可看出第二、三阶振型的响应量较小,因此振型耦合程度弱,计算误差并没有随着地震动峰值的增加而增加.这也说明了多模态静力弹塑性分析方法对于规则结构和以长周期为主的地面运动具有较好的精度,能满足工程需要.
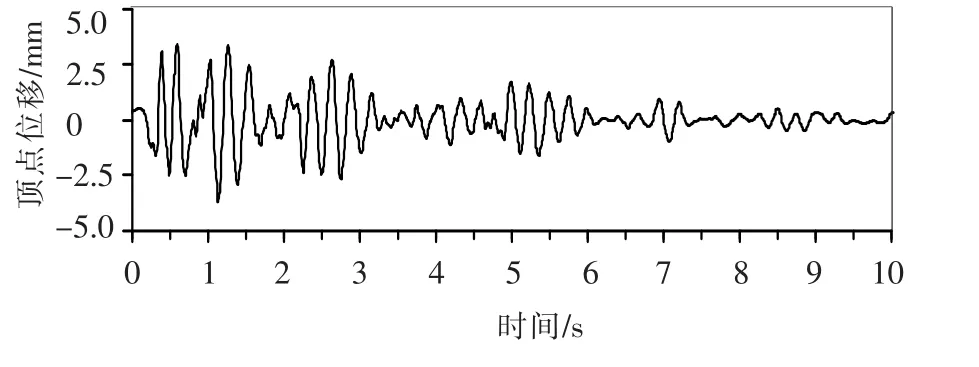
图2 顶层X向位移的时程图
文献[14]指出传统的静力弹塑性分析方法不能正确地评估结构在近场地震作用下的抗震性能,可见地面运动对静力弹塑性分析方法的影响是不能忽略的.地面运动对高阶振型的敏感程度很大程度上决定着模态坐标之间的相对耦合程度和静力弹塑性分析方法的适用性.为了验证地面运动对高阶振型敏感程度对计算结果的影响,用同一条实际地震波,通过改变地震波数据点的间隔时间,来改变地震动的频谱特性,从而增加对高阶振型的敏感程度.表5为Kobe地震波加速度数据点间隔时间的不同压缩比例对各个等效单自由度相对响应大小的影响程度和相对于弹塑性时程分析方法计算误差的关系,由表中数据可明显地看到随着地面运动频谱特性的改变,第二、三阶振型的相对响应量逐渐增加,引起的计算误差也逐步增大.

图3 多模态静力计算方法和弹塑性时程分析的计算结果对比
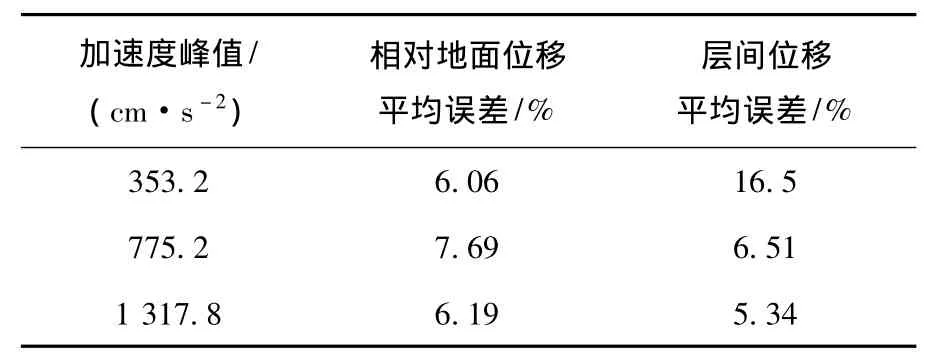
表3 多模态静力计算方法在不同地震动峰值下的计算误差
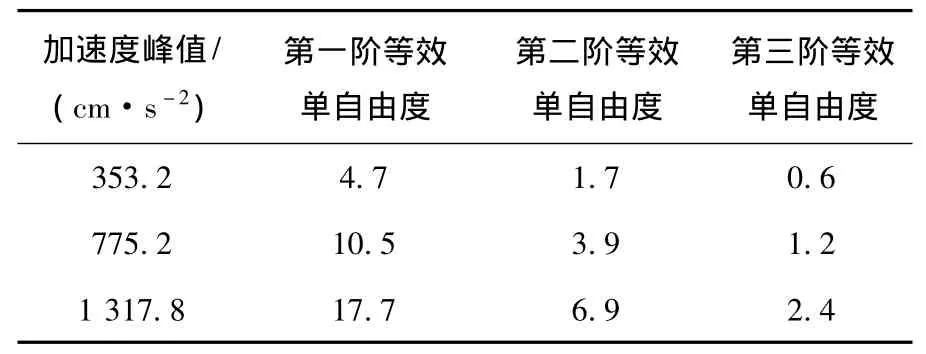
表4 前三阶等效单自由度的顶点位移
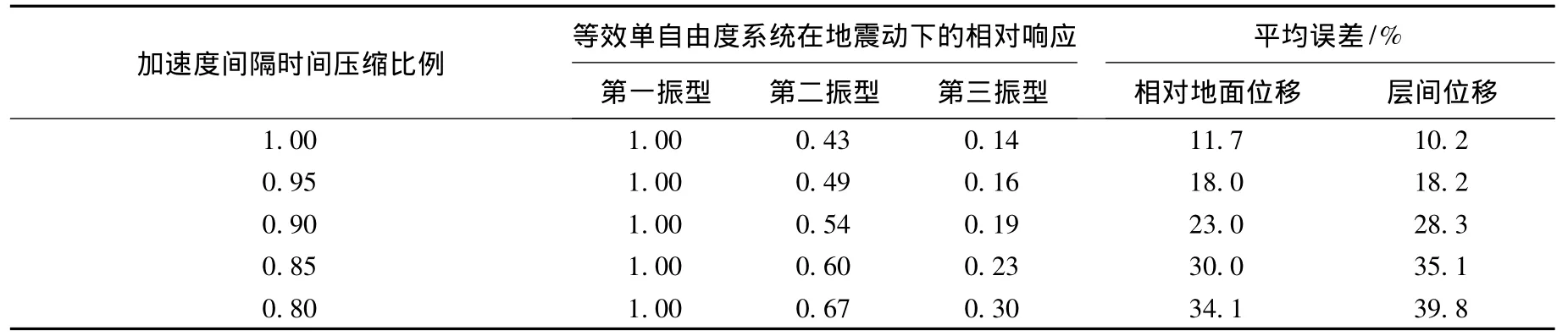
表5 地面运动频谱特性对多模态静力弹塑性分析方法精度的影响
图4为Kobe波加速度数据点间隔时间压缩为0.5倍时,各层平均层间位移误差随地震动加速度峰值的变化规律.由图中可看出当地面运动对高阶模态激励明显时,造成的误差随着地震动峰值的增加而增加,即各模态坐标之间的耦合程度随着结构非线性行为的发展而越来越严重.
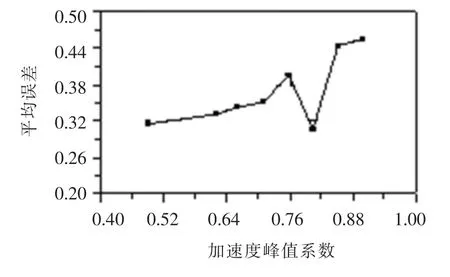
图4 地面运动强度对多模态静力弹塑性分析层间位移计算精度的影响
由以上分析可看出影响模态坐标耦合程度的主要影响因素为地面运动对高阶振型的相对激励程度,对高阶振型越敏感,在结构非线性行为发展过程中耦合程度越大.如地面运动对高阶振型的相对激励程度很小,即使结构的非线性行为发展得很严重,其振型耦合程度也不大,因此造成的计算误差较小.在地面运动对高阶振型的相对激励较大时,其耦合程度随着地面运动强度的增加而增加.
2.2 不同计算方法的对比分析
多模态静力弹塑性分析方法的主要缺点是没有考虑结构非线性行为发生后结构动力特性的改变,采用初始模态坐标解耦,造成各个模态等效单自由度之间的耦合,产生误差.因此改善多模态静力弹塑性分析方法应着眼于如何确定模态坐标,尽可能地减轻结构在非线性行为发生后各个等效单自由度之间的耦合程度.本文采用迭代的思路提出如第2节所示的改进的多模态静力弹塑性方法,对其在地面运动对高阶振型敏感程度不同的情况分别进行了计算分析.
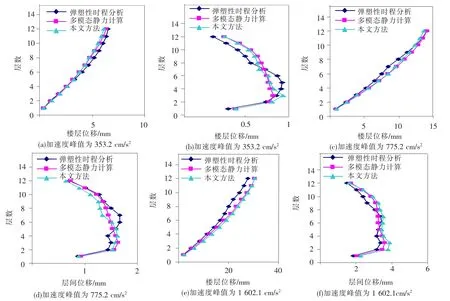
图5 不同计算方法在Kobe波不同峰值作用下计算结果的对比
图5为在Kobe波不同加速度峰值作用下分别采用弹塑性时程分析、多模态静力弹塑性分析方法和本文的改进多模态静力弹塑性分析方法进行计算结果的对比.由图5可看出对于一般对高阶振型不敏感的地面运动作用的情况,本文方法和多模态静力计算方法的计算精度(相对于弹塑性时程计算方法)相当.
图6为Kobe波加速度时间间隔压缩为0.5倍,不同加速度峰值时,本文方法和多模态静力弹塑性分析方法计算的层间位移相对于弹塑性时程计算方法的误差对比.因为静力弹塑性分析方法计算的层间位移较相对地面位移误差要大,因此图中数据仅给出层间位移的对比结果.表6为地震动加速度峰值为1 500 cm/s2时,各层的相对地面位移和层间位移多模态计算方法和本文方法的计算误差对比结果.由图6和表6中对比结果可以看出在地面运动压缩比例为0.5时,两种方法计算的误差都很大,这是因为对加速度时间间隔压缩为0.5倍以后,地面运动对高阶振型的相对激励程度就很大,因此振型耦合程度也很大,也说明了地面运动特性对静力弹塑性分析方法的影响很大,但是本文方法在所列四种情况下的计算精度都比多模态静力计算方法改善很多,验证了本文方法的适用性要优于传统的多模态静力计算方法.
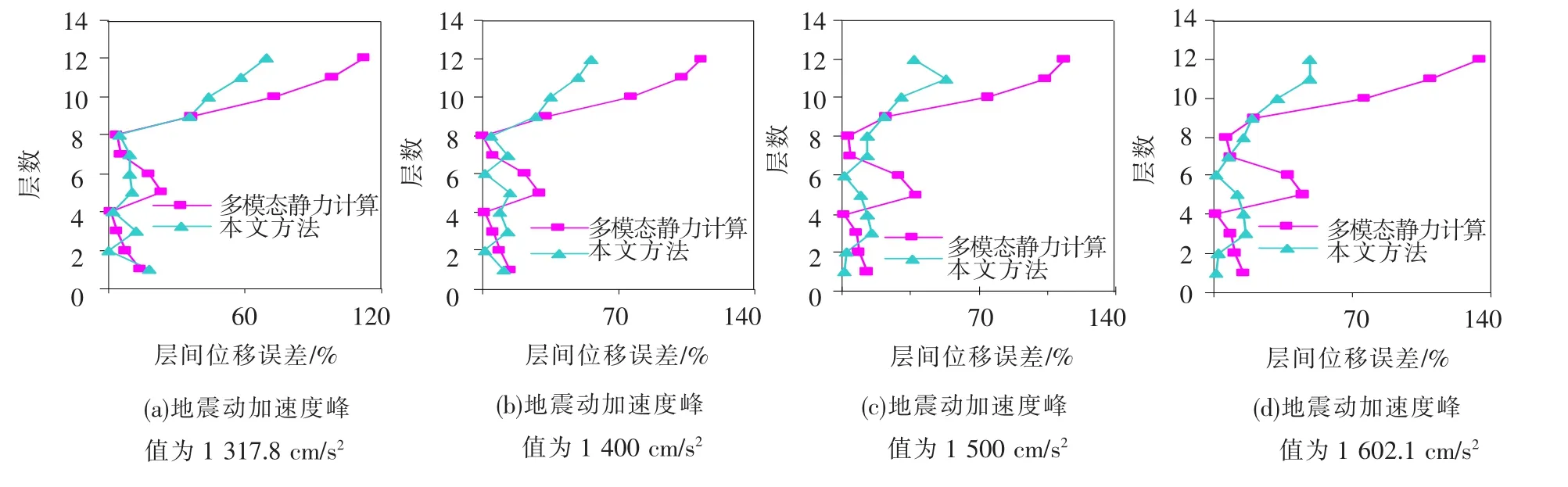
图6 不同计算方法在Kobe波不同峰值作用下计算结果对比
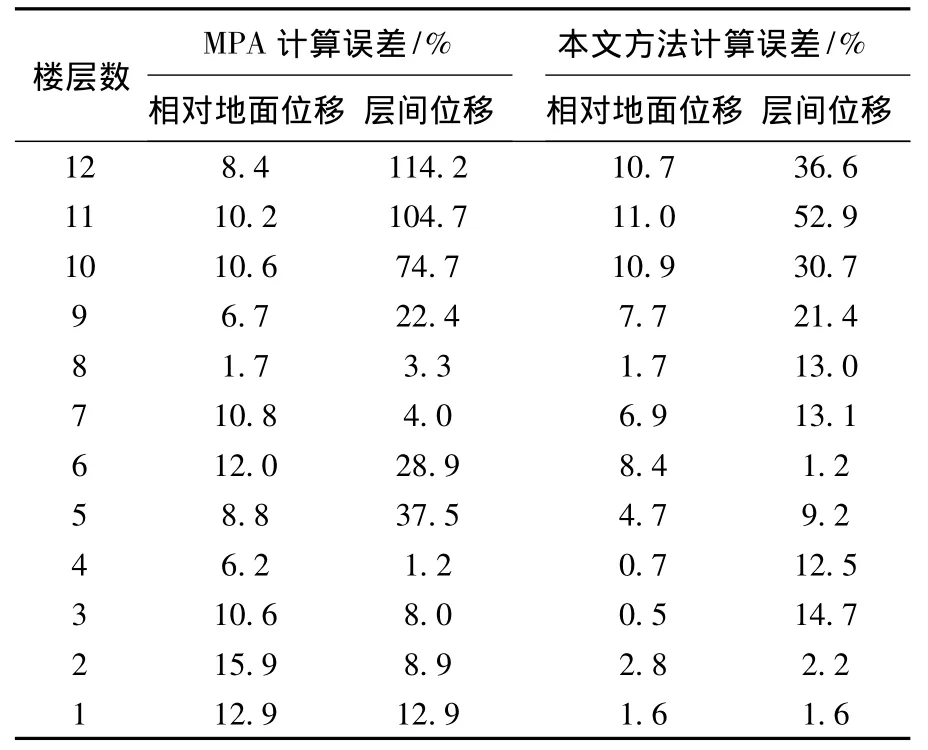
表6 本文方法和MPA方法计算误差对比结果(地震动加速度峰值1 500 cm/s2)
图7为Kobe波加速度时间间隔压缩为0.5倍,加速度峰值为1 317.8 cm/s2时,采用多模态静力弹塑性分析方法不同组合振型数和动力时程分析方法层间位移计算结果的对比图.由图中可看出当高阶振型的相对激励较大时,三阶振型的计算精度要差于两阶振型的计算结果.
3 结论
1)影响静力弹塑性分析方法精度和适用性的主要影响因素是地面运动的频谱特性,即地面运动对结构高阶振型相对激励的大小程度,如地面运动对高阶振型的激励较大时,即使结构为规则结构误差也很大.
2)如地面运动对高阶振型的相对激励较小,即使结构的非线性行为发展的程度很大,模态坐标之间的耦合程度也较小,即结构非线性行为的发展并不能明显改变多模态静力弹塑性计算方法的计算精度.

图7 不同振型组合数和动力时程计算结果的对比
3)当地面运动对高阶振型的相对激励较大时,计算精度可能随着组合振型数的增加而降低.
4)本文提出的考虑地面运动建立等效单自由度的多模态静力弹塑性分析方法,可改善静力弹塑性分析方法在地面运动对高阶振型相对激励较大时的计算精度,可增加静力弹塑性分析方法的使用范围.
5)随着地面运动对高阶振型相对激励程度的增加,两种静力弹塑性分析方法的计算结果将严重失真,所以静力弹塑性分析方法不能应用于地面运动对高阶振型相对激励程度很大的情况.
[1] 周定松,吕西林.延性需求谱在基于性能的抗震设计中的应用[J].地震工程与工程振动,2004,24 (1):30-38.
[2] CHOPRA A K,RAKESH K G.A modal pushover analysis procedure for estimating seismic demands for buildings[J].Earthquake Engineering and Structural Dynamics,2002,31(3):561-582.
[3] GOEL R K,CHOPRA A K.Evaluation of modal and FEMA pushover analyses:SAC buildings[J].Earthquake Spectra,2004,20(1):225-254.
[4] GUPTA B,KUNNATH S K.Adaptive spectra-based pushover procedure for seismic evaluation of structures[J].Earthquake Spectra,2000,16(2):367-391.
[5] GOEL R K,CHOPRA A K.Role of higher-mode pushover analyses in seismic analysis of buildings[J]. Earthquake Spectra,2005:21(4),1027-1041.
[6] HERNANDEZ-MONTES E,KWON O S,ASCHHEIM M A.An energy-based formulation for first and multiple mode nonlinear static(pushover)analyses[J].Journal of Earthquake Engineering,2004,8(1):69-88.
[7] 易伟建,蒋蝶.一种基于滞回耗能的改进pushover分析方法[J].自然灾害学报,2007,16(3):104-108.
[8] CHOPRA A K,GOEL R K,CHINTANAPAKDEE C. Evaluation of a modified MPA procedure assuming higher modes as elastic to estimate seismic demands[J].Earthquake Spectra,2004,20(3):757-778.
[9] JAN T S,LIU M W,KAO Y C.An upper-bound pushover analysis procedure for estimating the seismic demands of high-rise buildins[J].Engineering Structures,2004,26(1):117-128.
[10] 卢文生,吕西林.框架剪力墙结构模态静力非线性抗震分析方法研究[J].地震工程与工程振动,2005,25(1):58-66.
[11] 卢文生,吕西林.模态静力非线性分析中模态选择的研究[J].地震工程与工程振动,2004,24(6): 32-38.
[12] ANTONIOU S,PINHO R.Development and verification of a displacement-based adaptive pushover procedure[J].Journal of Earthquake Engineering,2004,8(5):643-661.
[13] KALKAN E,KUNNATH S K.Adaptive modal combination procedure for nonlinear static analysis of building structures[J].Journal of Structural Engineering,ASCE,2006,132(11):1721-1731.
[14] 易伟建,张冰.近场地震作用下框架结构的损伤机理[J].自然灾害学报,2007,16(2):112-117.
[15] KALKAN E,KUNNATH S K.Assessment of current nonlinear static procedures for seismic evaluation of buildings[J].Engineering Structures,2007,29 (3):305-316.
[16] 吕西林,李培振,陈跃庆.12层钢筋混凝土标准框架振动台模型试验的完整数据[R].上海:同济大学土木工程防灾国家重点试验室,2003.
[17] 徐福江,钱稼茹.常延性系数弹塑性位移谱及其应用[J].工程力学,2007,24(6),15-20.
[18] 吕西林,周定松.考虑场地类别与设计分组的延性需求谱和弹塑性位移反应谱[J].地震工程与工程振动,2004,24(1):39-48.
