样本选择模型及其估计方法＊

张 磊 王 彤

样本选择模型 (sample selection model)源于芝加哥大学的 James J.Heckman教授在 20世纪 70年代中期所从事的关于劳动供给的大量研究。1974年,他在《Shadow Prices,Market Wages,and Labor Supp ly》一文中通过对妇女劳动力供给与市场工资关系的研究提出样本选择模型及其似然估计,但因其估计方法复杂、计算量大等原因使得该模型并未得到重视〔1〕。稍后的五、六年间,Heckman对该模型的估计方法做出了进一步发展,终于在 1979年首创样本选择模型的两步估计,即著名的“heckman correction”。此后的二十年间,样本选择模型在劳动力供给、消费、教育、出生率和种族、性别歧视等诸多方面研究得到了极大的应用。自2000年始,国外医学领域已逐步将样本选择模型用于解决医学问题如医疗费用、生存质量评价和 HIV检验方法评价等,而该模型在国内医学领域的应用尚未见报道〔2-4〕。

样本选择模型的主要价值在于它可以有效校正抽样设计无法消除的样本选择性偏倚。例如在慢性疾病医疗费用的研究中,常将医疗费用作为因变量而家庭收入等影响因素(x′i)作为自变量建立研究所需的回归方程,即结果等式。事实上,我们仅能收集到确实去就诊患者的医疗费用(yi),无法获得确诊但不选择住院或其他治疗的这部分病人的医疗费用,这样就发生了样本选择偏倚。是否住院治疗是一种选择,每一个人都会很谨慎地评估它的成本和效益,而不太可能以丟硬币这样完全随机的方式来决定是否住院治疗,故而缺失的那部分应该发生的医疗费用通常不是理论上假设的完全随机缺失 (MCAR,missing completely at random)。每个确诊病人都会根据自身状况(z′i)(如家庭收入、婚否和知识程度等)来拟定出一个“承受费用”。确诊病人只有在发现住院费用(c)不高于承受费用时才会选择住院治疗;否则,不选择住院治疗。即每个确诊病人是否住院是根据承受费用和真正住院医疗费用(c)的比较来决定。而每个确诊病人的承受费用(d＊i)与该病人的自身状况(z′i)也可建立回归方程,即选择等式。由于仅能观察到确诊病人是否住院(di)而无法获得承受费用(d＊i)的信息,所以可以将二分类变量(di)作为选择等式的因变量构造出 Probit或 Logit模型。那么在给定z′i后,选择等式的回归系数γ和误差项vi以及界值c都决定了个体被选入可观测样本(di=1)的概率。γ值越大,则个体被选入样本(di=1)的机会越大,医疗费用被观测到的(yi=y＊i)可能性越大。而c值越大,个体被剔出样本(di=0)的机会越大,医疗费用缺失(yi=0)的可能性越大。如果γ=0,则个体是否被选入样本是随机的,仅受样本含量的影响。如果c取 -∞,无论γ值多大,所有个体都会被选入样本;如果c取 +∞,无论γ值多小,则所有个体都会被剔出样本。然而,仅基于上述可观测到的有偏样本(di=1)来估计结果等式是存在偏倚的。这样就可以构建出样本选择模型的基本结构:(1)是理论上存在的结果等式,(2)是因变量无法观测到的选择等式。(3)和 (4)分别反映了di和以及yi和的对应关系。当≥c时,di=1则yi=否则,di=0则yi=0。样本选择模型要求εi和vi相关且E[εi|vi]≠0。由于结果等式中x′i和 εi相关且εi和vi也相关,应用最小二乘估计无法获取一致的参数估计量β,故衍生出有关该模型估计方法的大量研究。

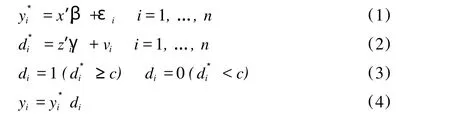
估计方法

一、似然估计

1.参数方法

Heckman和 Gronau率先引入似然估计。该法需对误差项分布做出如下假设 A:εi和vi服从均数为 0的双变量正态分布,且相关系数介于 0～1之间。在假设 A成立的条件下,应用似然估计来获取模型参数是最优的,且该法常作为检验其他估计方法功效损失的一个参考。当误差项不服从双变量正态分布但分布型已知时,可通过对应分布型的逆标准正态分布函数将结果等式与选择等式的误差项转换为双变量正态分布后仍选用似然估计。

2.半参数方法

尽管转换分布的方法并不严格要求误差项服从正态分布,但仍需要获得误差项边缘分布的信息。Gallant和 Nychka提出的方法可以不需要获得误差项分布的任何信息而产生一致估计量〔5〕。该法通过将误差项的联合密度函数近似为 Hermite级数来构造受限形式的似然函数,进而获得联合密度函数和模型参数的一致估计。通过实例分析发现在背离正态分布的假设下,应用该方法是有效的。但是由于该法涉及较多数学理论且计算相对复杂,所以在实际应用中比较少见。

二、两步估计

似然估计对于初始值的选择比较敏感,并且样本选择模型的对数似然函数常不是全局凹的,因而无法保证似然函数的解唯一,所以该法在实际应用中也受到局限。而最常见的估计方法是 Heckman提出的两步估计。依据误差项的分布假设,两步估计可分为基于双变量正态分布的参数两步估计和不要求分布假设的半参数两步估计。

1.参数两步估计

参数两步估计仍要求误差项服从双变量正态分布即上述假设A。两步估计的具体计算可归纳为以下几个步骤:①将有二分类因变量的选择等式构建成 Probit模型,然后应用最大似然估计获得选择等式参数的一致估计量。由于γ和σv常以比值形式出现,所以在样本含量为n的完全样本中,可应用似然估计来获得。Probit模型的对数似然函数是严格凹的,所以最大似然估计量γ是唯一的。②通过估计量γ获得每个人的预测值(z′iγ-c)/σv后 ,将其密度函数与分布函数的比值 ,构造出 λ((z′iγ-c)/σv)。 ③在因变量可观测到的有偏样本中,将σερεv^λi作为校正项加入结果等式后 ,应用最小二乘获得 σερεv和 β的一致估计量〔6〕。

参数两步估计假设误差项服从双变量正态分布,本质上是要求误差项间的关系是线性的,即εi是vi的线性函数。由此可以考虑适当放宽vi的分布做出假设 B:vi的分布已知且εi是vi的线性函数。如vi服从正态分布就意味着εi和vi服从双变量正态分布,这时假设 A等价于假设 B。由于假设 B允许vi服从其他分布,所以对选择等式可以构建除 Probit以外的其他模型。如vi服从均匀分布,可应用线性概率模型中最小二乘残差的简单变换来代替 λ((z′iγ-c)/σv),然后仍应用两步估计来获得一致估计量。当然,也可以对误差项进行分布转换来应用参数两步估计。

2.半参数两步估计

参数两步估计对分布假设异常敏感的特性限制了该法的应用,故而在样本选择模型问世后的二十多年里,一直有学者致力于研究对分布假设较为稳健的半参数两步估计。与参数两步估计不同,半参数两步估计仅需做出假设 C:E[εi|zi,di=1]=g(z′iγ),其中g是未知函数。参数两步估计中可通过双变量正态分布的分布假设详细刻画出校正项g(·),即σερεv^λi。但是半参数两步估计对于校正项的具体形式并不作要求。此外,半参数两步估计不需要利用vi的分布来获得选择等式估计量,且不需要通过误差项的分布关系来获得校正项。而半参数两步估计正是围绕着这两个“不需要”发展起来的,且这类估计方法的核心大致分为以下两个方面:选择等式回归系数γ的估计和校正项的估计。

(1)选择等式回归系数γ的估计

为了避免对误差项分布的过分依赖,常在第一步中对选择等式应用一些半参数或非参数估计方法来获得回归系数γ。自 20世纪 80年代始,二分类选择概率模型的估计方法在不断完善,所以对选择等式回归系数γ的估计方法也在逐步发展。以下对文献中所选用的方法作简要介绍:

Cosslett首先通过应用非参数最大似然估计 (nonparametric maximum likelihood estimator)来获得选择等式回归系数^γ。Powell、Stock和Stoker选用的平均导数估计 (average derivative estimator)计算相对简单,但是要求自变量是连续的。Kim和 Pollard选用最大得分估计 (maximum score estimation),但由于该法所获估计量^γ不是连续和渐近正态的,故不能应用标准的最优化方法。为了避免最大得分估计量的不连续性,Horowitz提出光滑最大得分估计 (smoothed maximum score estimation)。尽管该估计量是一致和渐近正态的,但是窗宽的选择相对困难〔7〕。此外,Ahn和 Powel选用非参数 Kernel估计方法 (nonparametric kernel estimation method)要求选择等式的误差项是连续分布。Ichimura通过应用对分布不作要求的半参数最小二乘法 (SLS)和加权半参数最小二乘法 (WSLS)不仅可获得一致和渐近正态的^γ估计量,且可获得协方差阵的一致估计〔8〕。另外,Klein和 Spady引入了轮廓似然估计法(profile likelihood estimator)来获得选择等式的回归系数,且所获估计量是一致和渐近正态的,同时还可以计算出相应的半参数可信区间。此外,该方法还可以解决多分类和有序分类的选择问题〔9〕。

(2)校正项的估计

在获得选择等式回归系数^γ的基础上,如何估计校正项是比较棘手的。事实上,样本选择模型的半参数两步估计难点就在于如何沟通选择等式与结果等式之间的关系,即在未知分布的基础上如何获得校正项的一致估计。对于校正项的估计,众多学者包括Heckman本人都做出了深入的研究:

Heckman和 Robb率先提出样本选择模型的半参数两步估计。该法通过对选择等式应用非参数方法获得回归系数估计量^γ,然后进行傅里叶级数展开近似获得校正项。Newey应用类似的方法在获得校正项的同时,还可以直接计算出结果等式的协方差阵〔10〕。Powell和 Robinson则是依据差分思想,比较结果等式中因变量存在缺失和不缺失对象的差别,来达到消除校正项的目的。而 Ahn和 Powell在此基础上还引入了加权变量〔11〕。Ichimura与 Lee对选择等式和结果等式的联立方程,应用迭代非线性最小二乘法,可获得参数的一致估计。

综合上述估计方法,Marcia Schafgans将半参数两步估计归纳为:第一步,可选用多种半参数估计法如最大得分估计、光滑最大得分估计、轮廓似然估计、半参数最小二乘估计和平均导数估计等。由于最大得分估计量不是渐近正态的,光滑最大得分估计中参数窗宽的选择比较困难,平均导数估计要求自变量是连续的,所以上述三种方法在实际应用中并不推荐。而轮廓似然估计和半参数最小二乘估计则由于所获估计量是一致和渐近正态的,所以在实际应用中较为常见。第二步,存在以下两种估计方法:(1)级数近似法该法利用第一步所获的γ估计量进行级数近似来估计校正项后,应用最小二乘来获得参数一致估计量。(2)核回归估计该法通过核回归估计来获取校正项,进行差分后构造新的结果等式。

小 结

由于似然估计的计算需要占用大量时间,而两步估计的计算相对简单,所以最初对样本选择模型的估计方法常选用两步估计。但是随着计算机技术的发展和软件包 (L IMDEP等)的开发,两步估计与似然估计在计算上所需的时间相差无几,但是许多学者仍然选用两步估计。这主要是由于两步估计还具有似然估计所不具备的优势:①当样本含量很大和参数数目较多时,似然估计比两步估计的计算仍要复杂很多,且样本选择模型的对数似然函数常常不是全局凹的,故无法保证似然函数的解是唯一的。②似然估计对于参数估计初始值的选择是比较敏感的,常需要给出一个好的初始值才能获得较好的估计量,而两步估计可以为似然估计提供可靠和有效的初始值。③两步估计比似然估计更稳健。当结果等式的因变量存在测量误差时,似然函数常会被误设以至于最大似然估计量不一致。然而,由于测量误差会被吸收到结果等式的残差项中,则所获得的两步估计量是一致。由于两步估计与似然估计的比较中存在以上优势,所以两步估计已成为计算样本选择模型参数估计量的标准程序,但该法仍存在需要完善的地方:

(1)共线性问题

尽管大多数应用学者认为样本选择模型两步估计所获估计量是完美的,但仍有部分学者基于两步估计中存在的共线性问题而心存疑虑。事实上,许多统计学家对两步估计中存在的共线性问题均给予了极大的关注,并提出了相应的解决办法。在样本选择模型的建模过程中,常发现选择等式的自变量向量和结果等式的自变量向量常是类似甚至是相同的。由于两者之间存在一定程度的相关性,且校正项在特定的取值范围内与选择等式的自变量向量呈线性关系,那么结果等式的自变量向量与校正项间也存在某种程度的相关性,故对结果等式的估计极易产生共线性问题,而共线性问题又会导致较大标准误以致所获估计量不稳定。

(2)异方差问题

如果随机误差项的方差不是常数,即对不同的自变量观测值彼此不同,则称随机项具有异方差性,这也是两步估计过程中亟待解决的问题。两步估计中,对结果等式标准误估计是比较复杂的。由于样本选择模型要求两等式残差项不独立,那么结果等式的方差很难退化为标准的方差 -协方差阵,且结果等式中常存在异方差性。显而易见,结果等式中V(εi)并不是常数项,它是随着选择等式自变量向量和校正项的不同而不同。当校正项已知时,扩大结果等式可以通过广义最小二乘法来获得。但是当校正项未知且需要估计时,应用上述方法就不再适合。因此,众多学者都提出了解决办法如“sandwich”估计法和自助法等〔12〕。尽管对标准误的估计有多种解决措施,但是至今尚没有公认最优的方法,故在实例分析中,多数应用学家仍倾向于直接应用两步估计的渐近协方差阵来获取标准误。此外,由于异方差与分布假设紧密相关,所以在对分布不作要求的半参数两步估计中,异方差问题的解决也是比较棘手的。

在医疗费用调查研究中,每个病人常要面临住院与否这样的二分类选择,而且还要对多种医学检查如尿检、血检、X线和 CT检查等作出决策,这就意味着样本选择模型中选择等式的因变量可能为多分类的,可构建成多分类 probit(polychotomous probit)或多项logit(multinomial logit)模型。尽管我们可以将选择等式构建成有多分类因变量的离散选择模型,但是如何反映选择等式与结果等式的联系将是很困难的。因此,如何将样本选择模型与离散选择模型相结合可能会是该方法在医学应用问题中需解决的发展方向之一。

3.社会实践 PBL法

单纯的课内加强实践教学编排并不能让学生马上就会解决实际问题,还要定期组织学生上课期间或假期积极参与社会实践活动,并对学生在课堂上学会的基本理论进行实际应用指导,培养学生对实际问题的判断能力,缩短学生学习理论与实际工作应用的时间,从而为社会培养出实用型人才。我们在临床本科专业采用了“指定式”社会实践 PBL法,即指定调查方向,实践前一到两周教师将相关资料分发给学生,要求学生根据所提出的问题去调查、获取和分析数据并撰写论文;而在预防医学本科和劳动与社会保障专业采用“查阅文献 -开题报告 -讨论审核 -具体实施 -统计分析 -形成论文”这一完整的科研模式,让学生围绕问题从调查单位和对象的确定、样本的抽取、问卷的编写、发放、回收与审核、数据的录入、整理与分析、直到论文的撰写。这样,学生经过亲身参与统计设计与调查、收集、整理和分析的整个过程,就比较系统地掌握了统计工作的各个环节。经过社会实践活动,医学生接触和参与了实际的医学科研工作,既拓展了科学视野、锻炼了实践能力、激发了探索和学习的热情,又增强了学生运用统计知识处理实际问题的能力,更有利于培养医学生严谨的科研思维,使学生毕业后很快融入到实际工作中去。

我们利用上述 PBL实践教学法在我院临床、预防、市场营销和劳动与社会保障四个本科专业学生中试行。不仅提高了学生自主查阅资料、获取信息的能力,拓宽了学生的知识面,还提高了学生统计逻辑思维和综合分析的能力,并使学生在 PBL实践中学会与他人进行有效的沟通、交流与合作,改革效果初现。总的来说,PBL模式的实践教学激励了学生实践的主动性、积极性和创造性,推进了学生自主学习、合作学习和研究型学习。也鲜明地显示了实践课在培养学生创新意识、综合实践能力与科研能力,培养现代化应用型人才中的重要作用。PBL教学效果并非是一个短期效应,它对学生解决实际问题能力的培养需要一个长期的过程,而这种能力一旦形成则终身受益。

1.叶小华,部艳晖,李丽霞,等.信息时代提高医学统计学教学质量的探索.医学教育探索,2008,7(2):138-139.

2.孙亚林,贺佳,吴骋,等.构建《医学统计学》课程群的实践探索.西北医学教育,2008,16(6):1166-1168.

3.张罗漫,孟虹,孙亚林,等.信息化条件下《医学统计学》分层次多目标教学探索与实践.中国卫生统计,2009,26(3):311-312.

4.闫国立.中医院校医学统计学教学改革的探索与实践.中医药管理杂志,2008,16(11):834-835.

5.王春平,王汝芬,翟强.多媒体技术在医学统计学教学中的应用.中国卫生统计,2006,23(3):266-267.

6.Bhattacharya N,Shankar N,Khaliq F,et al.Introducing p roblem-based learning in physiology in the conventional.Indian M edical Curriculum.Natl M ed J India,2005,18(2):92-95.

7.邓海燕,姚良悦,马蓉.PBL教学模式在护理教学中的应用探讨.护理研究,2008,22(1):262-264.

8.胡良平,刘惠刚.统计学的三型理论及其在生物医学科研中的应用.中华医学杂志,2005,85(27):1936-1940.