组学数据的核主成分聚类分析的可视化方法＊

2010-03-11哈尔滨医科大学卫生统计学教研室150086

中国卫生统计 2010年6期

哈尔滨医科大学卫生统计学教研室 (150086) 孙萌张涛李康

采用核主成分分析法(kernel p rincipal component anal

ysis,KPCA)。近几年,核主成分分析法受到越来越多的重视,本文在简要介绍 KPCA原理的基础上,通过对模拟数据和实际数据的运算考核其可视化效果,并且对 PCA和 KPCA两种方法进行了比较。

基本原理

核主成分分析法是将核函数与主成分分析法结合,通过事先确定的非线性映射函数φ,将输入向量 Xk(k=1,2,…,m)映射到特征空间 H:φ(Xk)中,然后在该特征空间 H中对数据进行主成分分析〔1,2〕。通常情况下,我们并不了解变量间真正的关系,采用不当的非线性函数,反而使结果不理想,并可能引起维数灾难。核函数则可以避免上述问题,它把非线性变换后的高维空间的内积运算转换为原始空间中的核函数计算,不需要明确给出φ的具体形式,而是通过计算核函数K(Xi,Xj)的值来计算内积。核主成分分析方法不是基于变换后的特征空间的协方差矩阵来计算特征向量,而是先求出输入向量的核矩阵,在此核矩阵的基础上算得其特征向量和特征值,从而避免了直接在变换后的高维空间求特征向量的运算,大大减小了计算量。

KPCA法进行数据可视化分析的基本计算步骤简述如下:

(1)选定核函数,并以此来计算输入向量的核矩阵K;

(2)将 K矩阵中心化;

(3)按公式λiαi=Kαi计算矩阵 K的特征向量αi和特征值λi;

(4)为了确保原样本的非线性相关系数矩阵的特征向量为单位向量,还需将相应的αi通过进行规范化;

针对具体数据,核函数的选择是一个重要的问题,采用不同的核函数,可以构造原始变量不同类型的关系。任何一个函数只要满足M ercer条件,就可以作为核函数,常用核函数有多项式核函数、径向基核函数(RBF)、平方核函数和 Sigm oid核函数〔1,2〕。其中径向基核函数 (RBF)被认为是一个较为稳健的核函数。计算软件可以使用M atlab7.6.0核主成分分析工具包等程序。

模拟试验

模拟试验的目的是,在类间可分的情况下,考察核主成分聚类分析的可视化效果,并在相同条件下对PCA和 KPCA两种方法的可视化效果进行比较。

1.模拟实验 1

由图 1(a)和图 1(b)可见,当对分类有作用的差异变量间存在非线性关系时,KPCA的聚类可视化结果明显优于 PCA的结果。KPCA的分析结果不仅能够准确地反映两组的分类情况,而且组间的样品点相距较远,而 PCA两类的样品却混在一起无法分辨。

图 1 PCA和径向基 KPCA的两种可视化方法比较

2.模拟实验 2

在模拟实验 1的基础上,分别混入 m′=50,200,500,1000个与分类无关的正态变量作为干扰变量,PCA和 KPCA分析结果如图 2。结果显示,加入 50、200和 500个对分类不起作用的无差异变量时,KPCA仍具有显著的分类可视化效果,但随着无差异变量数目的增加 (如 m′=1000),其聚类效果会明显变差。

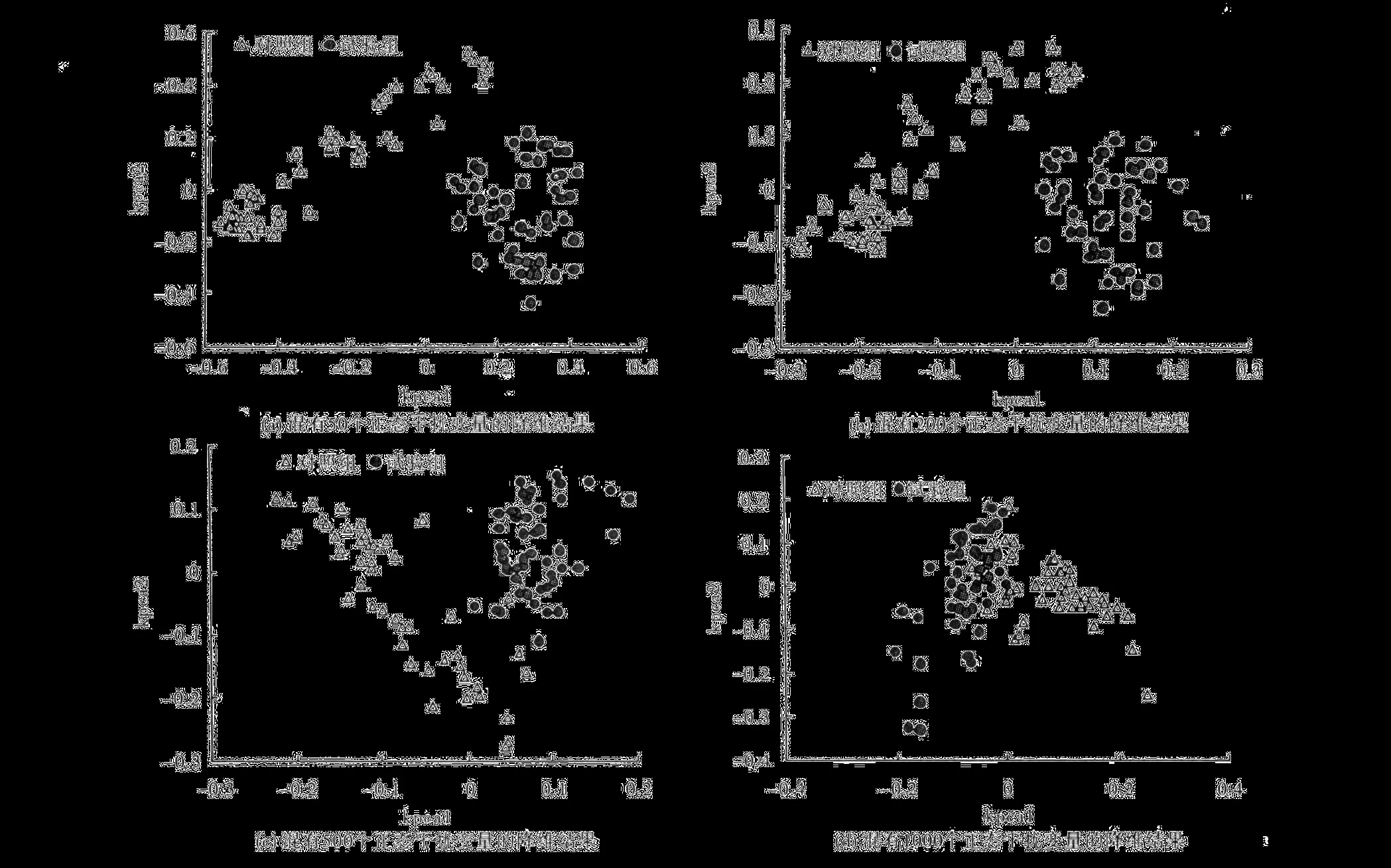
图 2 加入不同数目正态干扰变量时径向基 KPCA的可视化结果比较 (σ=8)

实例

为进一步研究核主成分分析法对高维数据的可视化效果,现选取一个真实的实验数据。实验分为对照组、服用营养素两组,每组各 10只小鼠,对其尿液的代谢组分用超高效液相色谱 -质谱联用仪进行检测,其中具有 886个代谢组分。在保持所有代谢组数据未进行变量筛选情况下,采用径向基函数作为核主成分分析法的核函数,比较 KPCA与 PCA的效果,结果见图3。结果显示,PCA的分析结果不够理想,但径向基KPCA分析结果则较好地表示出了两组的分类情况,说明其中可能含有具有生物学意义的代谢组成分。

小结

与主成分分析法不同,核主成分分析法能够解决变量间的非线性相关问题,其适用性更广。用核主成分进行聚类分析时,需要设置的参数很少,改变这些参数可以得到更好的效果,本文用模拟试验和实例说明了使用核主成分进行可视化分析的有效性。由于设定不同核函数的参数会产生不同的可视化效果,因此实际应用中需要确定最合适的核函数和参数。如果在作核主成分分析前,有针对性地对变量进行筛选,能够获得更好的可视化效果。