光纤光栅车辆称重测速关键装置设计与试验

2010-03-07张怀玉夏吉庆孟令权

东北农业大学学报 2010年12期

张怀玉，夏吉庆*，孟令权

（1.东北农业大学工程学院，哈尔滨 150030；2.黑龙江省计算中心，哈尔滨 150036）

车辆动态称重，即在非停车的运动状态下的称重。动态称重与传统的静态称重相比有许多优点，主要表现在节省时间、效率高、在称重时不至于造成交通拥堵[1-2]。目前国外产品的单轴载称重平均误差从±5.0%～±30%不等，相应置信度为90%或95%，最好的WIM（Weigh-in-Motion）系统单轴载称重误差可以控制在±5.0%以内[3]，但成本太昂贵仅适应于低速场合。本设计是将光纤布拉格光栅传感器埋入到复合材料中，制作成动态汽车秤，由于复合材料具有良好的耐腐蚀性，光纤光栅不需要单独的封装，使得整个结构能够应用于一些恶劣的环境，不受电磁干扰并且可以在完全浸水的环境下工作而不用特殊的维护，并且可以在车速较高的场合使用。本文旨在对复合材料秤体的研究进行阐述，解决了光纤光栅易损坏的问题。

1 材料与方法

1.1 试验材料

本车辆称重测速装置采用复合材料（由玻璃钢预浸料和碳预浸料等复合构成）制造，复合材料具有重量轻、刚度大，耐腐蚀的优点。称重传感器则采用FBR（光纤布拉格光栅），在试验时，把光纤Bragg光栅贴在秤体上，做成压力传感器，其工作原理是:光源发出的宽带光经光纤传输到被测量点，光栅有选择性地反射回一窄带近红外光[4-5]，经光分路器传送到波长鉴别器或波长解调仪，然后通过光探测器进行光电转换。当秤体受到外界压力产生形变时，光栅反射的窄带光中心波长会发生相应的变化，从而反应出秤体所受的相应压力[6-8]。FBR光纤光栅压力传感器具有灵敏度高、线性度好、结构简单、性能可靠、抗干扰性强等优点[9-12]。

1.2 试验方法

本试验通过应变反算载荷。为此把秤体简化为简支梁的形式，其一端采用固定铰支约束，另一端采用可动铰支约束。由于载荷的变化及传感器位置的影响，整个梁上各截面的剪力和弯矩有时不能由一个函数描述，因此根据不同情况分别加以考虑。为了计算载荷大小首先粘贴两个FBG传感器，假设简支梁长为l，以简支梁的固定铰支端为坐标原点，两个传感器距坐标原点分别为x1和x2，其中（x1＜x2），载荷F的加载位置为x。根据载荷的变化及传感器铺设位置，将分以下三种情况考虑。即①载荷F加载到两个传感器之间（x1＜x＜x2）、②载荷F加载到两个传感器左端（x＜x1＜x2）、③载荷F加载到两个传感器右端（x1＜x2＜x）。

下面重点介绍载荷F加载到两个传感器之间（x1＜x＜x2）的情况。

简支梁结构和载荷F的加载位置如图1所示。

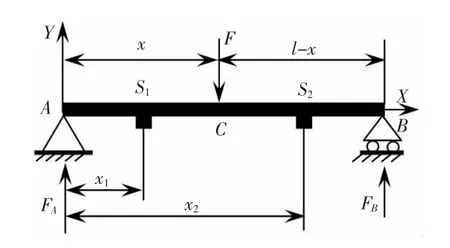
图1 简支梁结构和加载位置Fig.1 Simple beam structure and loading positions

材料力学分析可知，当载荷加载位置固定时（x为常量），应变与载荷呈线性关系；当载荷一定时（F为常量），加载位置x也与应变测量点的应变呈线性关系。这就是由传感器应变反算载荷的重要依据。

而在实际应用中，承重结构受到的力并不是集中力，而是小面积的均布力，当这个小面积的均布力可以看作由n个集中力组成，如图2所示（d为轮胎接地面的宽度，由于车型的不同、轮胎充气量的不同（d值会存在一定的差异，d作为常量考虑，d=200 mm）。

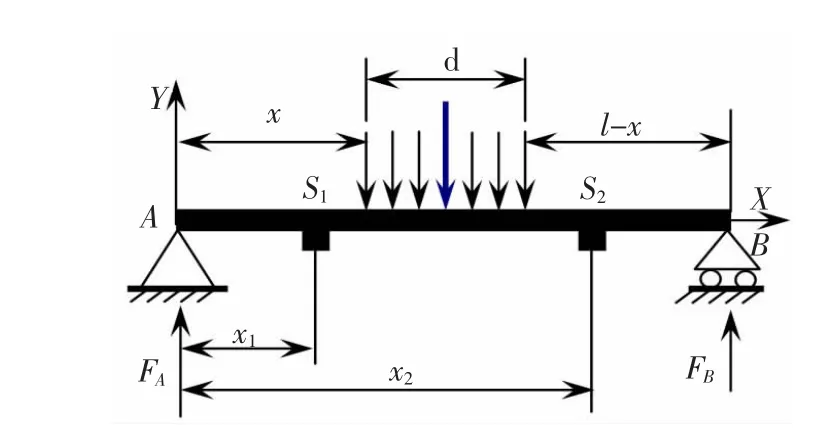
图2 均布载荷向集中载荷的等效Fig.2 Uniform load equivalent to the concentrated load

在计算中需要将公式进行修正，进行修正并整理后得到如下三组实用公式:

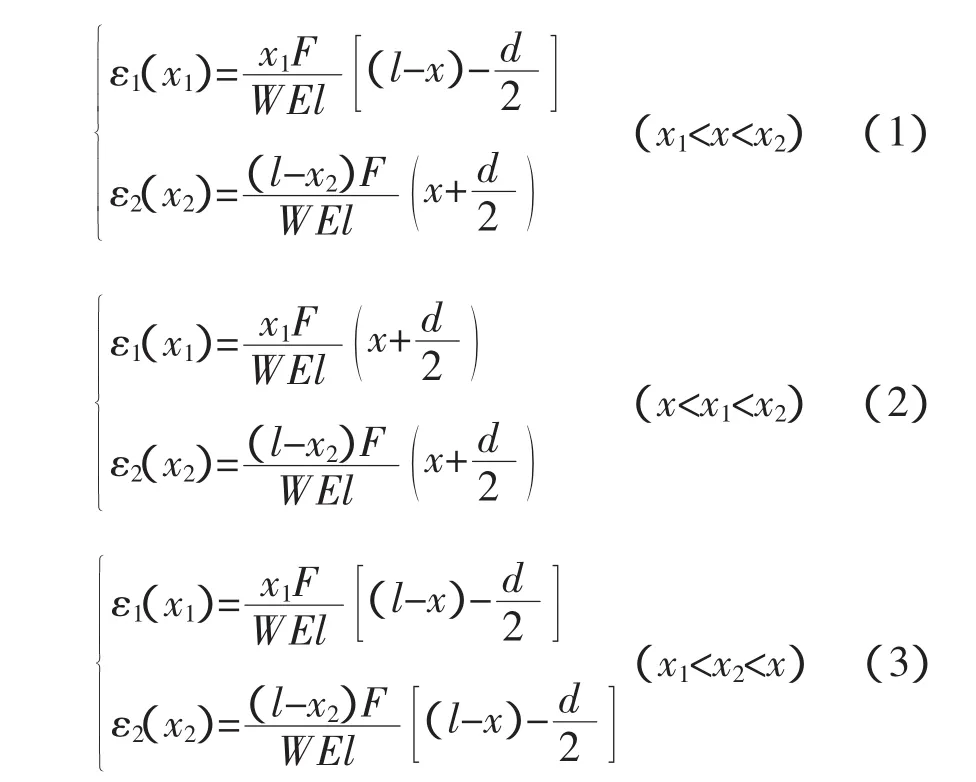
式中，W-抗弯截面系数（m3）；

E-弹性模量（MPa）。

从公式（1）～（3）可以看出，梁结构上加载的均布力与应变是一个符合ε=（kx+b）F关系的线性函数，当确定加载位置后，只要获得一个传感器的应变值就可以计算出所加载荷F；或者获得两个传感器的应变值就可以根据方程组分别计算出加载位置x及载荷大小F。这个线性函数中的斜率k，是一个与加载位置呈线性关系的函数，通过一定的静力试验测量获得的系统参数值会更真实，更实用。由于条件限制，研究只能在实验室进行秤体静力模拟试验，来获得秤体的固有参数。

1.3 试验安排

1.3.1 复合材料称体的结构设计与制造

结构设计决定了称体称重精度和载荷识别能力。称体的主承载结构为梁结构，这个梁结构一方面要具备足够的承载能力，一方面在载荷作用下要有一定规模的变形以保证测量的精度。这样，称体的刚度与测量精度成为一对互相牵制的因素:刚度大则测量精度低。在设计的过程中需要找到一个切入点使结构满足刚度要求并且具有足够的测量精度。综合考虑这些因素，称体的总体结构见图3。

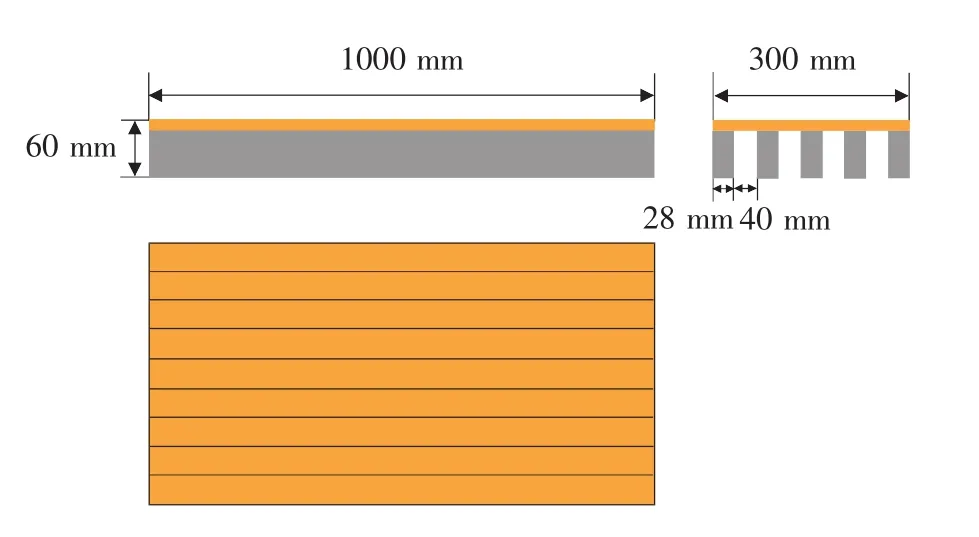
图3 称体的总体结构Fig.3 Scale structures

称体主要由面板和筋条组成，面板由玻璃纤维增强复合材料制造，筋条由碳纤维增强复合材料制造，其中有5根筋条，它们是主要承载的梁结构，当在其中一根梁上布置传感器时，可以测量整个加载于称体面板之上的载荷。复合材料汽车称实验件见图4。

图4 复合材料汽车称实验件Fig.4 Experiments pieces of compositematerials scale

1.3.2 静力试验

复合材料秤体静力实验主要通过对秤体不同位置加载时，测量主梁上各个传感器的应变响应，判断加载位置并换算出载荷。为了对秤体在加载过程中的变形情况进行掌握，在秤体的主梁粘贴光纤布拉格光栅应变片3个，秤体长度l取1000 mm，宽度取300 mm，S1、S2、S3分别粘贴在简支梁的300、500、700 mm 处，依据 ε=（kx+b）F 公式，分别对载荷作用的三种位置情况进行仿真，依次加载0.5 t，直到载荷5 t为止。具体实验步骤:

① 在 S2传感器附近加载，即 ε2＜ε1并且 ε2＞ε3的情况（具体x=400mm），使用公式（1）计算；

② 在 S1传感器附近加载，即 ε1＞ε2＞ε3的情况（具体x=200 mm），使用公式（2）计算；

③ 在 S3传感器附近加载，即 ε3＞ε2＞ε1的情况（具体x=600 mm），使用公式（3）计算。

对所测得的应变进行记录得到数据见表1。

对表1数据进行线性拟合，得到下列三组方程:

在传感器S1、S3之间加载方程:

在传感器S2、S3左侧加载方程:

在传感器S1、S2右侧加载方程:

把相应载荷代入上述三组方程，验证上述三组方程是否可行，得到如表2所示数据。

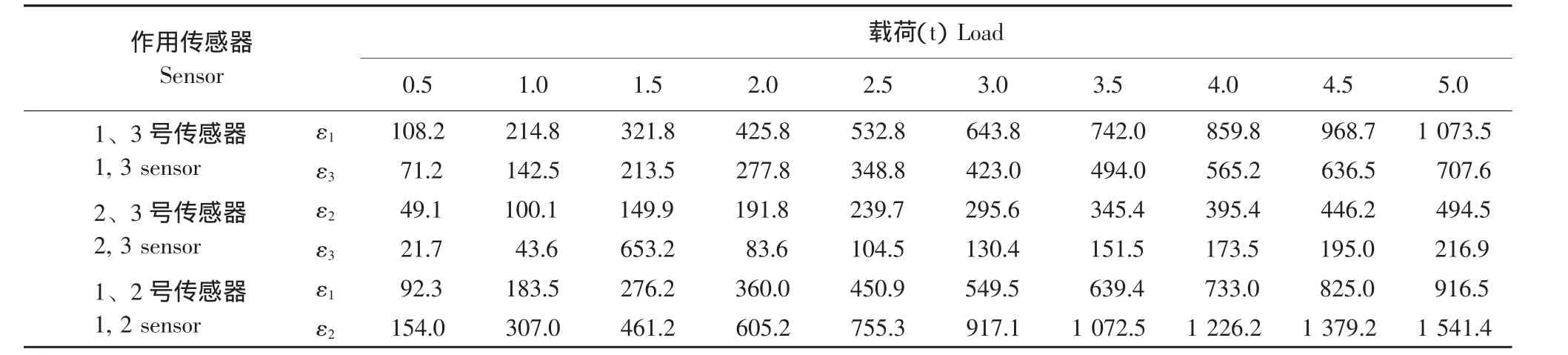
表1 载荷位置与传感器应变电压ε对应Table1 Load location and sensor strain ε correspondence (μV)

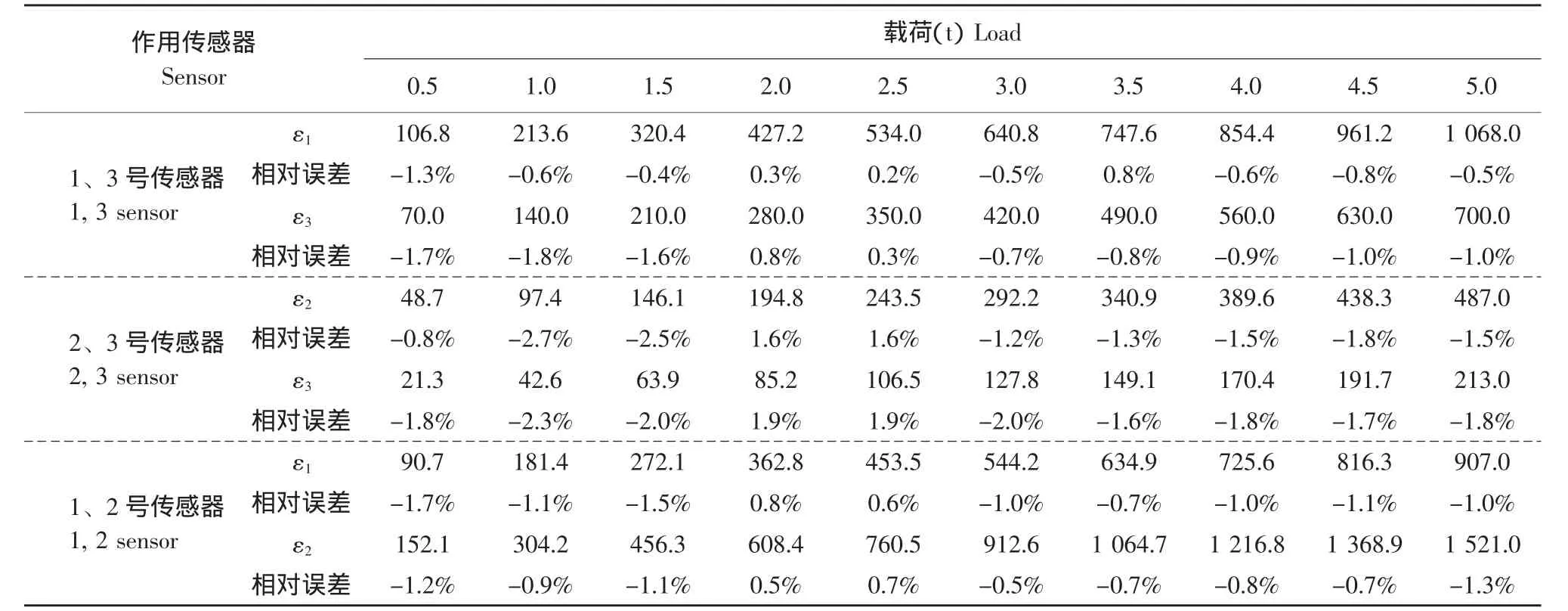
表2 由载荷与加载位置计算应变电压ε数据Table2 Calculated by the location of load and load strain ε data(μV)

1.3.3 复合材料秤体动态试验

为了开展复合材料秤体的路面动态测试，采用图5中所示的测试方案:①首先选择一个具有硬化路面，长度至少500 m状态良好的路段；②在实验路段上，按照国家的相关标准施工，建立秤体的混凝土基础；③使用专用的检衡车，通过向车内添减标准砝码，测试在不同速度下、不同载重下的秤体动态测重能力；④在秤体附近建立测试平台，集中测试设备对秤体传感器采集数据及光电测速数据进行采集。

1.3.3.1 秤体的标定和静态测量

静态测量是对秤体的标定，标定值作为标准值，便于动态测量值与其比较，计算动态测量误差。在动态实验开始实施之前，首先使用车载砝码对秤体进行简单标定，首先吊装车轮状的砝码分别置于A、B秤体上，由于轮形砝码本身形状的限制，秤体上只能安放一个，由于秤体对同一位置载荷的线性度，可以通过安放一个砝码使秤体产生的应变来检验载荷解算公式。通过方形砝码的累加来检验双轮上称时结构的线性情况。施加方形砝码首先加1 t，第二次加至3 t，第三次加至5 t，通过这三点的测量值可以拟合结构的线性斜率。针对传感器测量到的最大值拟合结果如图6所示。两称的斜率很接近，说明两秤体很稳定。

图5 动态试验的实施方案Fig.5 Dynamic experiment implementation plan

1.3.3.2 车辆动态测量

车辆动态测量数据记录在表3中。

1.3.3.3 动态数据的解算方法

实时监测软件采用Labview8.5编制[13]，软件采用PCI总线网卡实现和SI425光纤解调仪的数据传输，采用软件触发原理，实时捕捉称体所受外载荷时光纤应变状态。通过数值算法提取传感器的应变峰值和载荷时间，并计算车体的运行速度。根据动力学原理，利用称体结构和传感器分布位置反算出车体的重量[14－16]。

当车辆以一定的速度通过秤体时，光纤布拉格光栅传感器采集到的数据如图7所示，图中曲线按照时间顺序具有1、2、3、4四个峰值，说明该车具有四个轴，每个峰值应变是最关键的数据，将这些峰值应变代入到对应的公式（4）、（5）、（6）就可以计算出加在秤体上的载荷，对于同一轴重采用两个秤体测量，将两个秤体测量值相加就是该轴的轴重，将所有轴重相加就可以获得全车重量。至于车辆速度的测量，可以采用下述方法:由于秤体宽度一定，第一轴的车轮经过秤体的时间为t1，用秤体宽度除以t1就可以得到车辆速度。根据车辆速度还可以计算出某两个轴之间的轴距。由于同一轴使用两个秤体进行测量，通过车辆位置识别可以测出同一轴上的轮距。通过测量出的轴距、轮距与车型数据库内的信息进行比较，对车型做出正确判别，继而判断车辆是否超载。

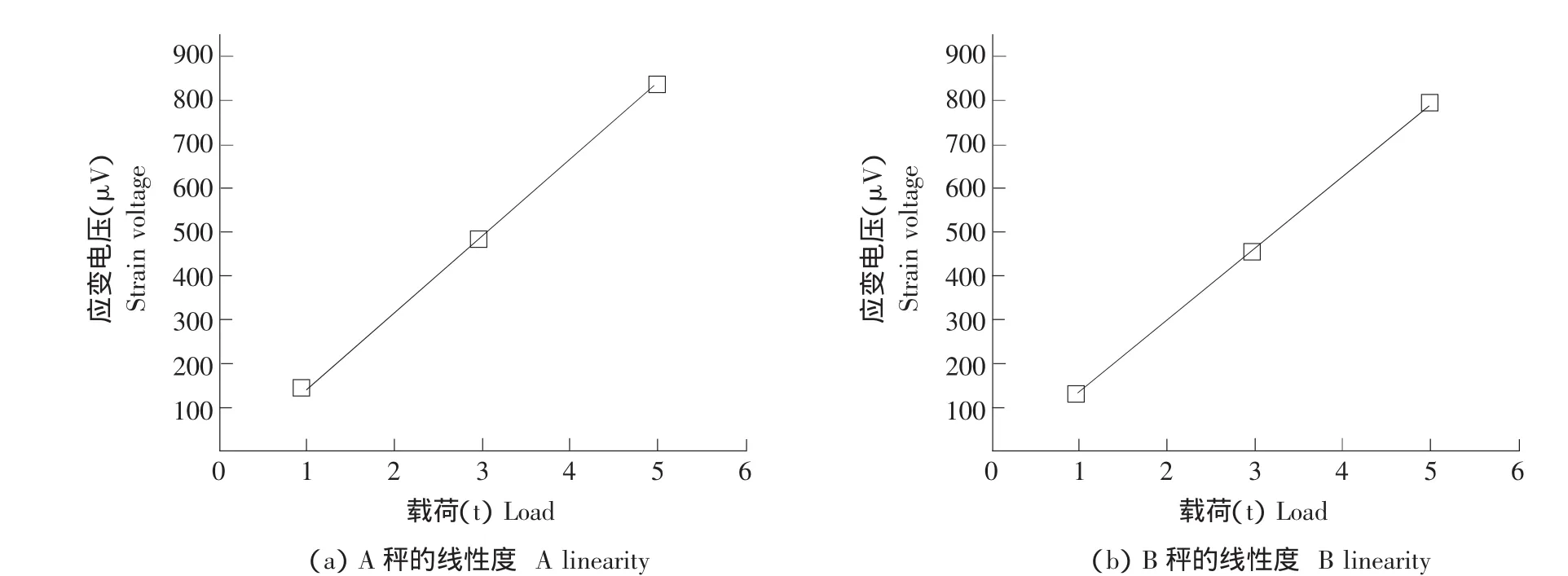
图6 双集中力作用下结构的线性度Fig.6 Linearity under the action of pairs concentrated force structure

2 分析验证

根据表1和表2的数据，对静力试验误差进行分析，得到应变的最大绝对误差 Δε =20.4，最大相对误差。

对表3车辆动态测量数据进行分析，在剔除粗大误差之后，得到载荷的最大绝对误差，载荷的最大相对误差

由分析结果可见，无论静力应变试验，还是动态载荷试验，相对误差都在设计要求的5%以内。

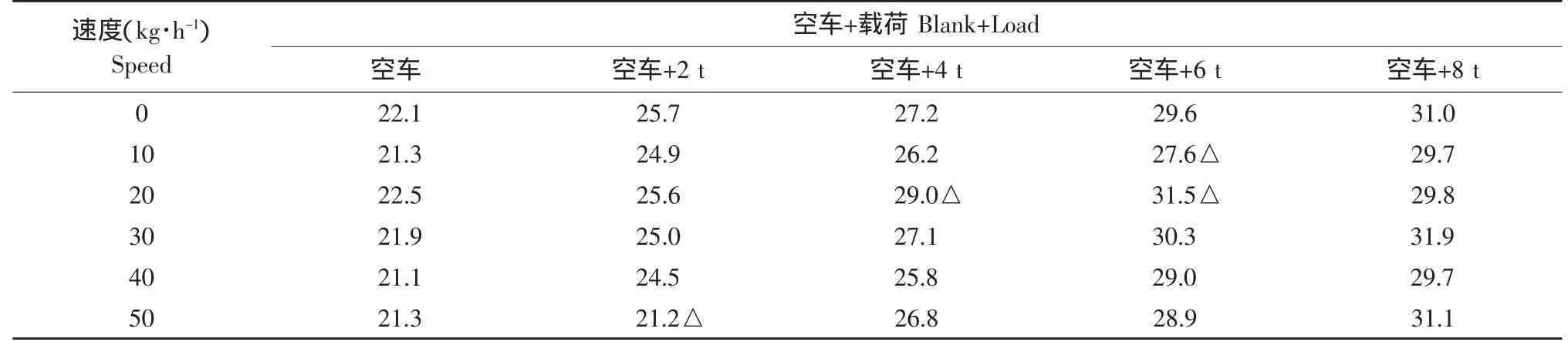
表3 动态测量记录数据Table3 Dynamic measurement record data (t)

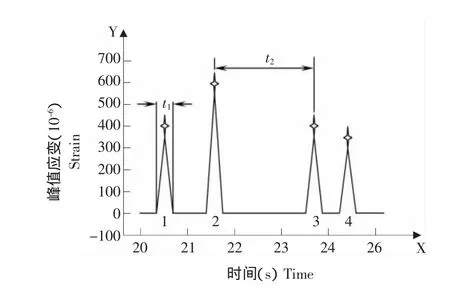
图7 测量获得的数据形式Fig.7 Measurement obtained data form

3 结论

a.以静态值为基准，测量的误差最大在2.7%，并且在增添砝码时，不同载荷下测量到的差值情况较稳定，秤体对载荷的变化敏感，系统误差在设计的范围内，完全满足设计指标。

b.动态实验的测量值具有一定的离散性，这种离散性对秤体称重的置信度有一定影响，主要有两方面原因:一是那些离散度很大的测量值都是车轮位置比较靠近秤体边缘的位置，也就是说车轮压在了称重无效区域，在这类位置，载荷的解算公式不再适用或已经误差很大；二是秤体本身在最初的设计时是针对单轮胎驶过秤体时的动态测量，实验中的检衡车第一轴、第二轴为单轮，第三轴、第四轴为双轮，对第一轴和第二轴的测量使用解算公式可以比较准确地进行，而对于第三、第四轴的测量只能利用砝码检称时的线性关系进行粗略测量，这是将来需要对秤体进行改进的地方。

[1]冯玉昌,史冬琳,冯锁丽,等.DSP在动态称重系统中的应用[J].仪表技术,2007(7):33-34.

[2]贺曙新.车辆动态称重技术的历史、现状与展望[J].中外公路,2004(12):104-108.

[3]周祖濂.高速公路管理与WIM技术[J].衡器,2007,36(5):2-5.

[4]燕昌江,李锋,徐良梅,等.近红外光谱技术在畜牧生产中的应用[J].东北农业大学学报,2008,39(11):140-144.

[5]宋一弘,刘文洋,杨宇姝.基于IPV6协议重构校园网的研究[J].东北农业大学学报,2006,37(6):853-856.

[6]陈宏波,蔡雄飞,姜德生.光纤光栅压力传感器的研究[J].武汉理工大学学报,2003,25(8):55-56.

[7]胡志新,张桂莲,张陵.基于薄壁应变筒的光纤布拉格光栅压力传感器[J].南京理工大学学报,2004,28(3):277-280.

[8]廖延彪.光纤传感发展近况[J].光电子技术与信息,2006(6):23-25.

[9]禹大宽,乔学光,贾振安.光纤光栅传感系统的现状及发展趋势[J].传感器,2005,24(3):4-6.

[10]魏鲁原,伍斌,崔霞.动态称重系统的设计[J].自动化仪表,2002,23(8):4-37.

[11]宋爱娟,闫冬梅.基于DSP的动态称重系统设计[J].仪器仪表学报,2003,24(4):115-117.

[12]杨亦飞,刘波,张伟刚,等.工程化光纤光栅应变传感器的制作及其应用[J].仪表技术与传感器,2005(4):1-2.