基于欧拉梁理论的管路纵向波功率流简化模型误差分析

刘 彦 周进华

中国舰船研究设计中心，湖北 武 汉 430064

基于欧拉梁理论的管路纵向波功率流简化模型误差分析

刘 彦 周进华

中国舰船研究设计中心，湖北 武 汉 430064

为分析基于欧拉梁理论的管路纵向波功率流简化模型的误差，首先基于壳体理论推导了充液管路纵向波功率流的精确模型，该模型解析和表述了管路材料、几何参数以及管内液体流速等因素与功率流之间的关系，通过与基于欧拉梁理论的功率流简化模型的对比即可得到简化模型的误差。理论分析与仿真结果表明：在低频区，基于欧拉梁理论的纵向波功率流模型误差近似为一恒定的常数，该常数与厚径比以及管路的材质有关，而管路半径以及管内流速对简化模型误差的影响可以忽略。

管路；功率流；简化模型；误差分析

1 引言

管路作为输送水、油、蒸汽的主要载体在化工、核电、船舶等领域发挥重要的作用，然而在其发挥主要功能同时也成为不必要振动和噪声的传输载体，严重影响了周围环境，甚至会因振动造成管路损坏而带来安全隐患。开展管路功率流测试是分析管路振动传递特性、控制管路振动的重要手段，因此管路功率流测量研究受到国内外学者的关注［1－4］。

目前对充液管路建模的精确理论无疑是壳体理论，而壳体理论认为管路存在无穷多个径向模态，而每个径向模态又对应无穷多轴向模态，尽管经过简化依然包含较多变量［5－7］， 不利用实际操作。因此，在工程上退而求其次，采用欧拉梁理论对充液管路进行简化处理，这势必会带来一定的误差，故有必要对该误差进行理论分析，为功率流测量精度的提高奠定理论基础。虽然国内外学者对基于欧拉梁理论简化模型的误差有过一定的分析［8］，但是这些分析都是定性的、片面的，目前尚没有对管路特性参数与管内液体流速等因素对简化模型误差的确切影响的研究。为了全面分析该误差，本文首先基于Flügge方程推导了充液管路纵向波功率流的精确模型，通过与工程上使用的基于欧拉梁理论的功率流模型对比，即可分析基于欧拉梁理论的简化模型的误差，通过分析得出了简化模型的应用范围以及注意事项，为纵向波功率流精确测试提供理论支撑。

2 理论模型

由于工程中使用管路的管壁远小于其半径，因此充液管路一般可等效为充液薄壁圆柱壳体，充液薄壁圆柱壳体的自由振动Flügge方程可表示为：

式中，a为壳体中性面半径；ν为泊松比；E为壳体材料的杨氏弹性模量；ρ为密度；h为壁厚；β2为厚度因子（β2＝h2／12a2）；Δ2是 Laplacian 算子（Δ2＝a（∂2／∂x2） + ∂2／∂θ2），U、V、W 分别为中性面上任意一点的轴向、切向和径向位移；x、r、θ为柱面坐标。具体情况如图1所示。

依据参考文献［9］～［11］，U、V、W 以及 P 具有以下的形式：

式中，kns为轴向波数；为径向波数，ρf为管内液体密度；cV为液体流速，J（·）为一阶贝塞尔函数。

将式（4）～式（7）代入式（1）～式（3）整理后可得充液管路系统的耦合模型的矩阵形式。

式中，Ω＝ωa／cL为无量纲频率；cL液体中的声速；FL为流固耦合项。

而流固耦合项可以用贝塞尔函数表示为：

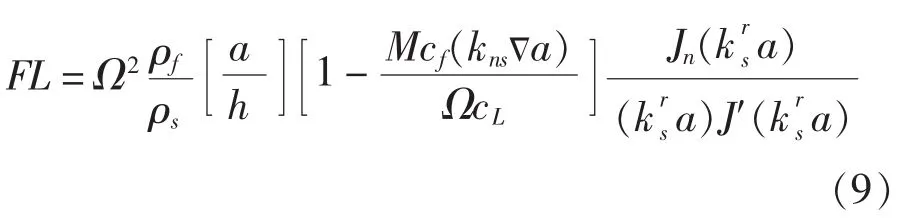
式中， M＝cV／cf为马赫数。

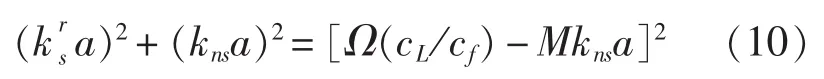
依据式（8）可得壳体中性面上的任一点三向位移之间的关系：

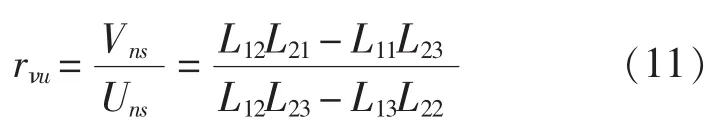
基于壳体理论的纵向波功率流可以表示为：

式中，〈A，B〉为 A和B的互谱；Nx为轴向力。

而壳体总轴向力可以表示为：

式中， D 为膜刚度，D＝Eh（1－ν2）

将式（14）带入式（13）整理后可得功率流表达式。

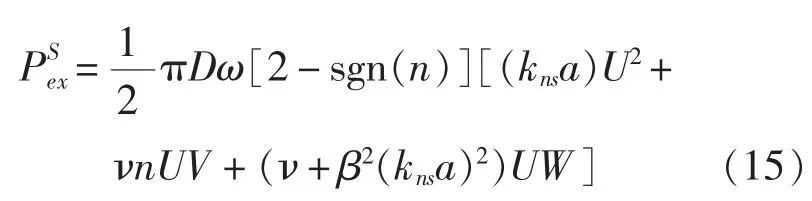
由于不同轴向模态之间没有能量交换，因此对于任意模态（n，s）有：

为了便于工程应用，往往利用梁模型理论对管路进行简化。依据欧拉梁理论，梁内仅存在相互解耦的纵向波、扭转波和弯曲波，而纵向波功率流可以表示为：

式中的k为波数，虽然基于欧拉梁理论获得的波数与基于壳体理论获得的波数具有一定的差别，但在工程测试时，无论用那种方法测量纵向波功率流，所用波数都是同一实测结果。因此，此处的波数k可以直接利用壳体理论所获得的kns代替。

在频率低于壳体一阶环频率时，壳体内可以传递能量的传输波只有n＝0时对应的扭转波（s＝0）、纵向波（s＝2）和 n＝1 时的弯曲波［9］，此时将式（16）和式（18）相除，并将式（11）和式（12）带入可得：

首先利用式（8）～式（10）求出沿管路传递的纵向波的波数 k02，然后结合式（11）～式（12）可以获得任一点三向位移之间的比值，将这些参数带入式（19）即可求得基于两种不同理论的纵向波功率流之比，而通过分析这一比值就可以得到基于欧拉梁理论纵向波功率流简化模型误差的变化规律。

3 数值仿真与分析

在工程实际中，应用最多的管材是不锈钢和硬橡胶，它们的基本参数如表1所示。下面就以这两种材料为研究对象，分析不同条件下的纵向波功率流简化模型的误差。

表1 材料的特性参数

首先分析不同厚径比（h／a）对功率流简化模型误差的影响。利用上一节推导的公式，分别求出h／a＝0.1、0.05 和 0.005 条件下， 两种模型所获得功率流比值随无量纲频率的变化情况，结果如图2所示。

由图2（a）可见，对于不锈钢材质管路而言，基于梁理论的简化模型获得功率流要大于基于壳体理论的精确值。随着厚径比的减小，功率流简化模型误差变化不是单调的，而是先变大然后再减小；而在厚径比相同的情况下，功率流简化模型误差都是随着无量纲频率的增加而增加。在所分析频段内误差保持在15%以内，而在无量纲频率0.3以下，误差随着频率变化很小，近似为常数。依据图2（b）可知，与不锈钢材质的管路相反，对于硬橡胶材质的管路而言，基于梁理论的简化模型获得功率流要小于基于壳体理论的精确值。随着厚径比的减小，功率流简化模型误差呈现单调递减的趋势。值得注意的是，在厚径比相同的情况下，简化模型的功率流误差在整个分析频段内基本保持恒定而与频率无关，因此在无量纲频率0.7以下，对简化模型的功率流进行简单修正就可以获得相应的精确值。

工程中应用的管道半径多为 0.01～0.1 m，对铁质管路而言，无量纲频率0.3对应的频率是25～2.5 kHz，对于硬橡胶材质管路而言，无量纲频率 0.7 对应的频率是16 ～1.6 kHz，而工程实际中所关心的频段主要集中在1 kHz以下。因此在工程实际中，可以直接使用基于欧拉梁理论的简化模型测量功率流，然后乘以一个修正系数就可以获得对应的精确值，这个系数与管路材质以及厚径比有关。

其次分析相同厚径比（h／a），不同半径对功率流简化模型误差的影响。对于厚径比比较小的薄壁管路而言，管路横截面积s≈2πah，带入式（19），整理后得：

由上一节的推导过程可知，管路系统的无量纲纵向波数k02a与无量纲频率Ω的关系受厚径比影响，而与半径无关，因此由式（20）可知，在厚径比相同且以无量纲频率Ω作为横坐标的前提下，半径的变化对功率流简化模型误差没有影响。需要注意的是，半径的变化会造成实际频率ω发生变化，因此在以实际频率作为横坐标的条件下，图2所示的一条曲线将变成一簇曲线，但变化趋势以及误差的最大值将不会发生变化。

最后，分析管内流速变化对功率流简化模型误差的影响。同样以不锈钢材质和硬橡胶材质的管路为研究对象，分别分析 h／a＝0.05，流速 v＝5 m／s、20 m／s、40 m／s情况下， 两种模型所获得功率流比值随无量纲频率的变化情况，所得结果如图3所示。

由于水中的声速v为1 500 m／s，因此所分析的3种流速条件下，对应马赫数都远小于1，对管路系统的纵向波数基本不产生影响，因此无论对于不锈钢管路还是硬橡胶管路系统，流速的变化对功率流比值影响都不大，亦即对简化模型的误差影响较小。在工程实际中管路中的流速通常小于5 m／s，因此流速的影响可以忽略不计。需要注意的是，这个结论是在无限长直管模型下获得的，因此只在长直管道成立，而在管路的弯管、变径等不连续位置处并不成立。

4 结论

本文分别基于壳体理论和欧拉梁理论建立了充液管路的纵向波功率流模型，并利用两者的比值定量分析了基于欧拉梁模型的纵向波功率流简化模型的误差随厚径比、半径以及管内液体流速的变化发生变化的情况，得到以下结论：

1）基于欧拉梁理论的纵向波功率流简化模型的误差随着管路材质与厚径比的变化而变化，对于铁质管路而言，基于欧拉梁理论测得的纵向波功率流将偏大，而对于硬橡胶材质管路则偏小，但在低频区，两种材质的管路都可直接使用基于欧拉梁理论的简化模型测量功率流，然后乘以一个修正系数即可获得对应的精确值，这个系数与管路材质以及厚径比有关。

2）对于相同的厚径比，纵向波功率流简化模型的误差随无量纲频率的变化情况与半径无关。

3）由于工程实际中管内流体马赫数远小于1，因而对较长的直管段进行纵向波功率流测量时，管内均匀流速的影响可忽略。

［1］PAVIC G.Vibration energy flow in elastic circular cylindrical shells［J］.Journal of sound and vibration，1990，142（2）：193－310.

［2］朱显明，张国良，黄其柏，等.均匀流管自由振动的能量分布特征［J］.振动、测试与诊断，1999，19（2）：95－99.

［3］THIEN A B，CHIAMORI H C，CHING J T，et al.The use of macro－fibre composites for pipeline structural health assessment ［J］.Structural control and health monitoring，2008，15（1）：43－63.

［4］KARAGIOZIS K N，AMABILI M，PAIDOUSSIS M P，et al.Nonlinear vibrations of fluid－filled clamped circular cylindrical shells ［J］.Journal of Fluids and Structures，2005，21：579－595.

［5］BREAVART B J， FULLER C R.Radial impusive excitation of infinite fluid －filled elastic cylindrical shells ［J］.Journal of sound and vibration， 1994， 177（3）： 411－422.

［6］XU M B.Three methods for analyzing forced vibration of a fluid－filled cylindrical shell［J］.Applied Acoustics，2003，64： 731－752.

［7］徐慕冰，张小铭，张维衡.充液圆柱壳中的振动能量流［J］.华中理工大学学报，1997，25（2）： 85－87.

［8］FINNVEDEN S.Simplified equations of motion for the radial－axial vibrations of fluid filled pipes ［J］.Journal of sound and vibration， 1997， 208（5）：685－703.

［9］FULLER C R，FATHY F J.Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid ［J］.Journal of sound and vibration，1982，81（4）： 501－518.

［10］BREAVART B J，FULLER C R.Effect of an internal flow on the distribution of vibrational energy in an infinite fluid－filled thin cylindrical elastic shell ［J］.Journal of sound and Vibration， 1993， 167（1）： 149－163.

［11］朱显明，朱英富，张国良.壳式管道管壁振动能量流的测量方法［J］.中国造船，2004，45（4）：29－34.

Error Analysis of Simplified Model Based on Euler Beam Theory for Power Flow of Longitudinal Waves in Pipes

Liu Yan Zhou Jin－hua
China Ship Development and Design Center， Wuhan 430064，China

In order to analyse the error of simplified model based on Euler beam theory for power flow of longitudinal waves in pipes， the exact model was developed firstly.based on shell theory， which shows the relationship among materials of pipes， geometrical parameters， internal flow velocity and power flow.Then the error of simplified model based on Euler beam theory can be obtained by comparing the simplified model with the exact model.Theory analysis and simulation results show that in low frequencies，the error of the simplified model is approximately a constant， which is determined by thickness－radius ratio and materials of pipes，and the effect of the radius and internal flow velocity on the error can be neglected.

piping system；power flow；simplified model；error analysis

TB532

A

1673－3185（2010）02－13－05

2009－05-06

刘 彦（1979－ ），男，博士，工程师。 研究方向：噪声振动控制。E-mail：liuyanhit＠gmail.com