考虑流体加载效应的板结构声辐射损耗因子和辐射效率的计算分析

黎 胜

1大连理工大学 工业装备结构分析国家重点实验室，辽宁大连 116024

2大连理工大学 船舶工程学院，辽宁 大连 116024

考虑流体加载效应的板结构声辐射损耗因子和辐射效率的计算分析

黎 胜1，2

1大连理工大学 工业装备结构分析国家重点实验室，辽宁大连 116024

2大连理工大学 船舶工程学院，辽宁 大连 116024

采用有限元法和Rayleigh积分耦合方法对考虑流体加载效应的板的结构声辐射损耗因子和声辐射效率进行了计算分析，其中结构振动模态的声辐射损耗因子和声辐射效率分别基于模型降阶的结构模态参数识别方法和考虑流体附加质量的实模态进行计算。对板在空气和水中的声辐射损耗因子和辐射效率进行了计算，计算结果表明：板的奇奇振动模态的声辐射损耗因子远大于其他类型模态；板奇奇振动模态在空气中的声辐射损耗因子远小于水中的声辐射损耗因子，约差一个数量级；板在水中的声辐射损耗因子远大于板的结构损耗因子，空气的声辐射损耗因子与结构损耗因子相当；空气中的声辐射效率比水中的声辐射效率约高两个数量级。

流体加载效应；声辐射；损耗因子；辐射效率

1 引言

结构的声辐射损耗因子和声辐射效率分别体现了流体附加阻尼的大小和结构声辐射能力的强弱，目前已有不少研究探讨了空气中结构的声辐射效率［1，2］，但对考虑流体加载效应的结构声辐射损耗因子和声辐射效率研究还不多见。众所周知，考虑流体介质加载效应的结构振动声辐射计算是一个结构—声耦合问题。对中低频激励作用下的结构—声耦合问题的求解，目前最有效、最能发挥求解方法自身优点的是耦合有限元／边界元方法，即结构问题用有限元法进行处理，声流体问题用边界元法进行处理［3］。常规的有限元／边界元耦合方法，其不足之处在于不能进行考虑流体加载效应的结构模态分析。GIORDANO等［4］和CUNEFARE等［5］采用激励频率的幂级数形式对声阻抗矩阵中的元素进行拟合，将声阻抗矩阵元素中隐含的激励频率用显式表示出来，再将激励频率的不同次幂项与速度的乘积用位移的不同阶导数表示后就消除了声阻抗矩阵的频率依赖性，然后在状态空间内将结构有限元方程和流体边界元方程耦合起来。此后，由状态空间特征向量的双正交性，通过求解一个标准的复特征值问题可以得到流体加载下结构的固有频率、振型和声辐射模态阻尼比等。考虑到声阻抗矩阵的频率依赖性来源于格林函数，黎胜［6］对 Giordano和 Cunefare的状态空间有限元／边界元耦合方法进行了改进，不采用拟合而是直接对格林函数进行最佳平方逼近或级数展开，直接得到不隐含激励频率的声阻抗矩阵，并直接对逼近误差和截断误差进行估算以保证模态分析的精度。李贤徽和黎胜［7］基于模型降阶法也实现了考虑流体加载效应的结构振动声辐射的模态参数识别。

本文采用有限元法和Rayleigh积分基于考虑流体附加质量的实模态和基于模型降阶的水下结构模态参数识别方法对空气和水中板结构振动模态的声辐射模态辐射效率和模态损耗因子进行了计算分析和比较，还对点力作用下的结构声辐射效率和损耗因子进行了计算分析。

2 理 论

2.1 结 构

结构在简谐激励力作用下，考虑流体加载效应的有限元形式的运动方程为：

式中， ω 为激励圆频率； i＝（－1）1／2； ［M］、［C］和［K］分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；｛x｝为结构位移向量；｛F｝为外激励力向量；［G］为转换矩阵，其作用是将结构表面法向力向量转换为与结构自由度对应的力向量；矩阵［A］＝∫S［N］T［N］dS，［N］为形状函数矩阵，S 为结构表面；｛p｝为结构表面声压向量。

2.2 声辐射

结构表面声压向量和表面法向速度向量的关系式可统一表示：

式中，［Z］为声阻抗矩阵；｛νn｝为结构表面法向振速向量。对嵌在无限大平面障板中的平板结构，式（2）可通过对板表面Rayleigh积分进行离散得到。对具有封闭表面的三维结构，结构表面声压和结构表面法向振速的关系式也可通过对表面Helmholtz积分方程进行离散得到。

2.3 结构声辐射的声辐射效率和损耗因子的计算

结构表面法向速度向量｛νn｝、结构有限元节点速度向量｛ν｝和结构位移向量｛x｝之间的关系式可表示为：

求出结构位移向量｛x｝后，进而可求出｛ν｝、｛νn｝和｛p｝等。结构的辐射声功率W可由结构表面声压｛p｝和表面法向振速｛νn｝通过下式求得：

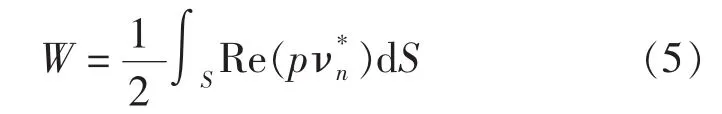
结构的声辐射效率一般定义为：

式中，W为结构的辐射声功率；ρ为流体介质的密度；c为流体介质中的声速；S0为结构的表面积；〈〉为结构表面法向振速均方值，定义为：

式中，νn为表面法向振速。

对板厚为h，密度为ρs的板结构，其声辐射损耗因子与辐射效率的关系为［8］：

声辐射损耗因子也可由结构辐射声功率和均方速度表示为：式中，M为结构质量。

2.4 结构振动模态的声辐射效率和损耗因子的计算

由结构表面声压向量｛p｝和表面法向速度向量｛νn｝的关系式，式（1）可用矩阵表示为：

式中，［R］＝（［A］／2）Re（［Z］）。 于是，｛νn｝又可以表示为：

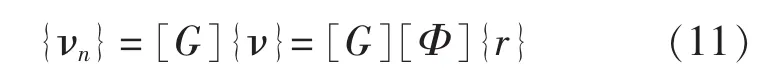
式中，［Φ］为结构振动模态矩阵（振型矩阵）；｛r｝为结构振动模态速度向量。所以，式（10）又可以表示为：

由式（12）可见，各振动模态对声辐射的贡献是不独立的，［T］的对角元素体现了各阶振动模态自身对结构辐射声功率的贡献，而非对角元素则体现了各阶振动模态间的耦合对结构辐射声功率的贡献。

对空气中结构的振型矩阵采用真空中的模态矩阵［Φ］，即求解广义特征值问题：

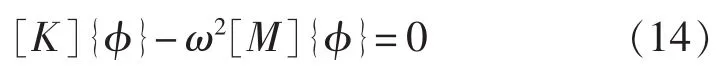
得到结构振动的固有频率ωi和固有振型｛φi｝。对水中的模态矩阵，由于与水中模态固有频率ωi对应的流体附加质量矩阵为［9］：

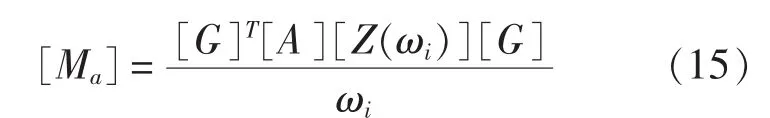
求解由［K］和［［M］＋［Ma］］确定的广义特征值问题即可得到与 ωi对应的模态矩阵｛Φi｝。 ｛Φi｝为不考虑流体附加阻尼的实模态矩阵。

各阶振动模态的辐射效率可由辐射效率的定义式（6）求得：

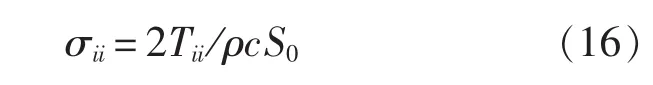
对模态阻尼损耗因子的计算，考虑流体加载效应的结构—流体耦合系统的降阶模型的刚度阵和质量阵中的分块为：

式中，H（ω） ＝ ｛F｝T（-ω2［M］ ＋iω（［C］ ＋ ［G］［A］［Z］［G］T）＋ ［K］－1）｛F｝，ωαωβ为计算频段内的插值频率。在计算频段内根据式（17）和式（18）来形成降阶模型的刚度阵［K^］和质量阵［M^］后，求解由［K^］和［M^］确定的广义复特征值问题即可以得到在计算频段内流体加载下结构振动模态的固有频率和声辐射损耗因子等模态参数。

3 数值算例和分析

3.1 结构声辐射的模态损耗因子和模态辐射效率

矩形板板长 Lx＝0.455 m， 板宽 Lν＝0.379 m，板厚 h ＝0.003 m， 板密度 ρs＝7 850 kg／m3，E ＝2.1×1011N／m2，ν ＝0.3， 边界条件为四边简支，空气密度 ρ＝1.21 kg／m3，声速 c ＝343 m／s，水密度ρ＝1 000 kg／m3，声速 c＝1 500 m／s。 参考声功率取为10－12W。计算中采用四边形四节点等参元对结构进行离散，网格为16×16，其中有限元为基于Mindlin板弯曲理论的板元，板表面Rayleigh积分的离散使用和有限元计算同样的网格。表1列出了考虑流体加载效应的板在空气中和在水中的前五阶振动模态的固有频率和声辐射损耗因子。

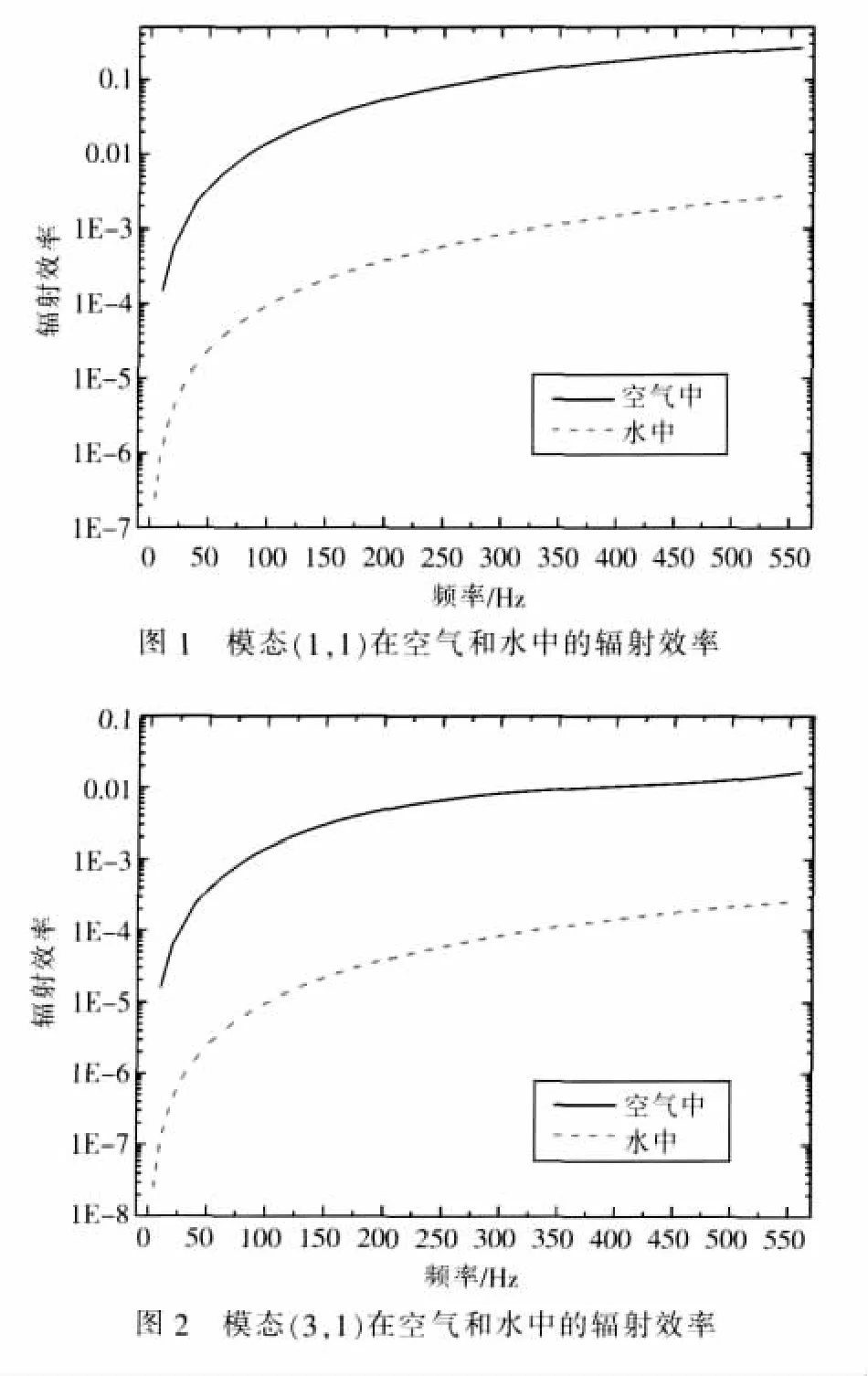
由表1可见，考虑空气的加载效应后得到的固有频率与真空中的基本一样，即空气的附加质量效应可以忽略，结构在空气中各阶振动模态的声辐射损耗因子有较大差别，奇奇模态最大，奇偶模态和偶奇模态次之，偶偶模态最小，最大的第1阶振动模态的声辐射损耗因子为0.001416。各阶振动模态声辐射损耗因子的差别实际上是由各阶模态的声辐射能力决定的，辐射效率高的模态声辐射能力强，相应地损耗因子大。从表1还可以看到，水的附加质量效应使结构的固有频率大大降低。结构在水中各阶振动模态的声辐射损耗因子较空气中有更大差别，奇奇模态（1，1）和（3，1）的声辐射损耗因子分别为0.012和0.0084，奇偶模态、偶奇模态、偶偶模态的声辐射阻尼损耗因子与奇奇模态的声辐射损耗因子相比非常小。对比空气和水中（1，1）模态的声辐射损耗因子，水中的声辐射损耗因子约大一个数量级。计算奇奇模态（1，1）和（3，1）在空气中和在水中的模态辐射效率如图1和图2所示，可以看到，空气中的模态辐射效率远远大于水中的模态辐射效率，约高两个数量级。虽然水中的模态辐射效率小于空气中的辐射效率，但由于水的特性阻抗较大，较小的速度就可以辐射出较大的能量，所以表1水中奇奇模态的辐射损耗因子大于空气中的损耗因子。关于辐射效率，损耗因子和特性阻抗的具体关系也可参见式（8）。

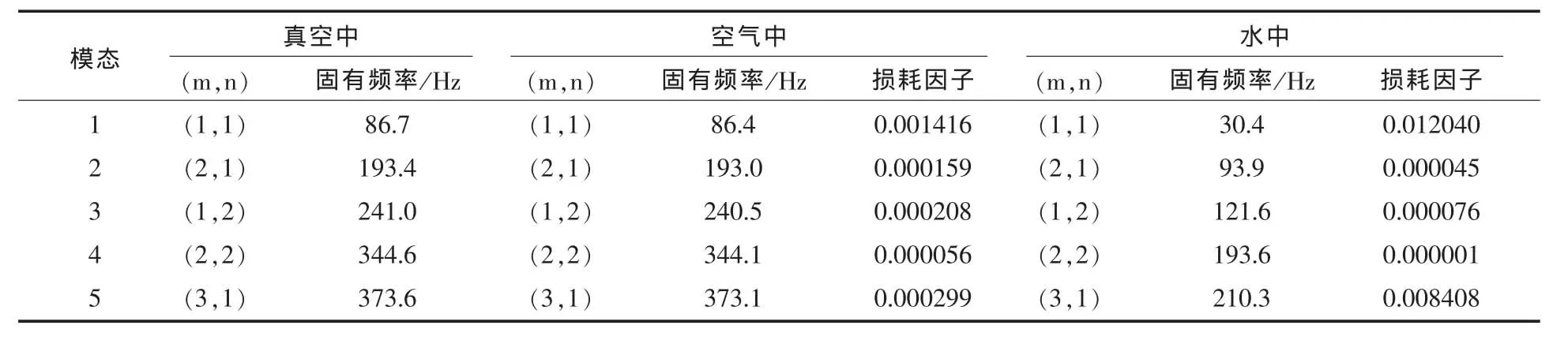
表1 空气和水中板振动模态的固有频率和声辐射损耗因子

3.2 结构声辐射的损耗因子和辐射效率

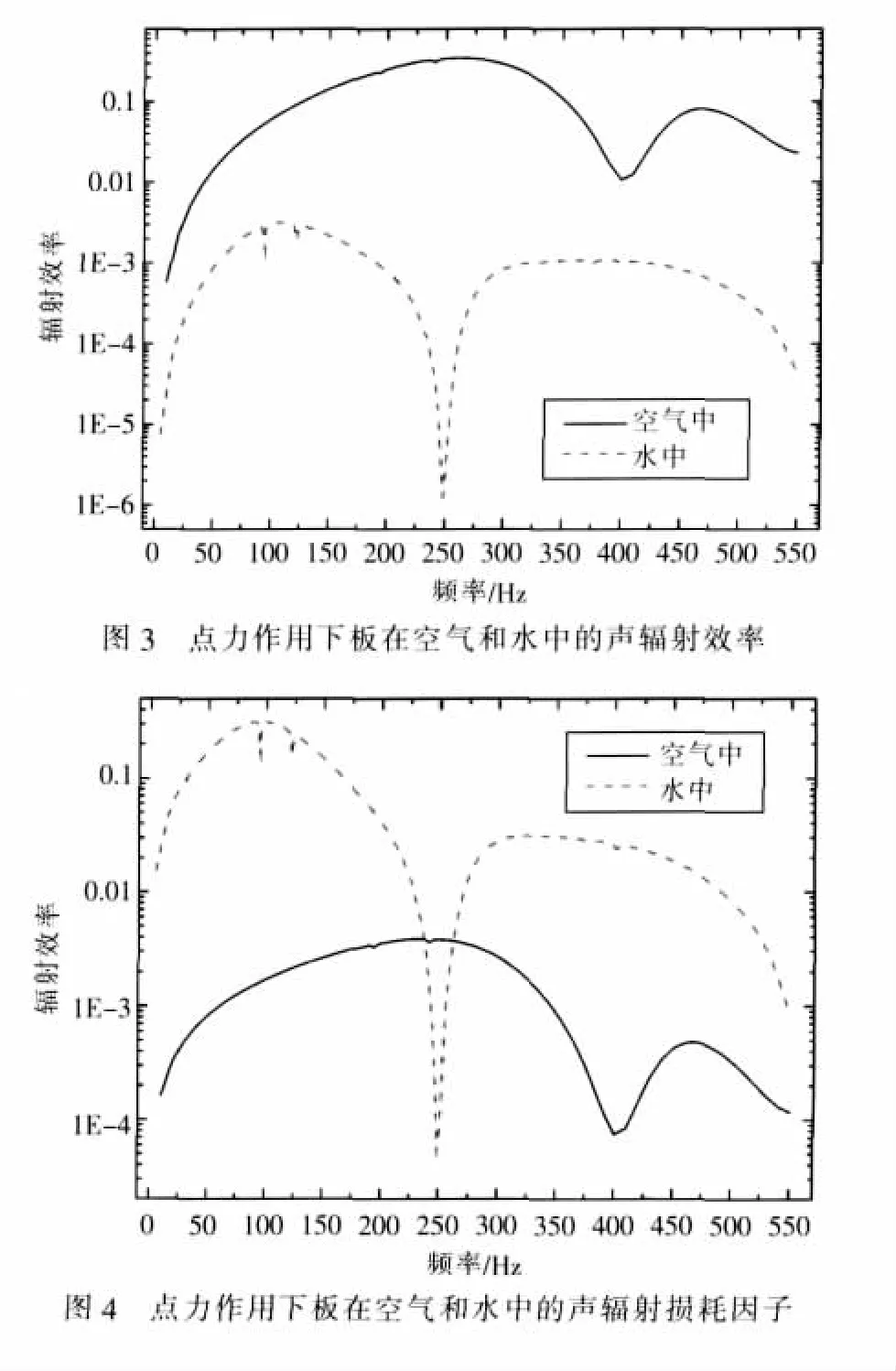
计算矩形钢板在垂向点力激励 （力幅值F0＝1N）的作用下，作用位置为板中心时激励频率从5 Hz到550 Hz间的辐射效率和辐射损耗因子如图3和图4所示。由图可见激励力作用下结构的声辐射效率和声辐射损耗因子在空气中和在水中均有较大差别，水中的声辐射效率约为0.001量级，空气中的声辐射效率约为0.1量级，水中的声辐射损耗因子基本上大于0.01，空气中的声辐射损耗因子约为0.001量级。这样，如取钢材的结构阻尼损耗因子为 0.0013［10］或1 ～ 6 × 10－4［11］，则水的声辐射阻尼的作用远大于结构阻尼的作用，空气的声辐射阻尼的作用与结构阻尼相当。空气中的声辐射效率约为0.1，较之约为0.001的水中声辐射效率高两个数量级。

4 结论

本文采用有限元法和Rayleigh积分基于考虑流体附加质量的实模态和基于模型降阶的水下结构模态参数识别方法对考虑流体加载效应的板结构振动模态的辐射效率和损耗因子进行了计算研究，还对点力作用下的结构声辐射效率和损耗因子进行了计算分析。计算分析表明：板的奇奇振动模态的声辐射损耗因子远大于其他类型模态；板奇奇模态在空气中的声辐射损耗因子远小于水中的声辐射损耗因子，约差一个数量级；板在水中的声辐射损耗因子远大于板的结构损耗因子，空气的声辐射损耗因子与结构损耗因子相当；空气中的声辐射效率比水中的声辐射效率约高两个数量级。本文中所给出的空气和水中的声辐射损耗因子和辐射效率对板结构声辐射阻尼的选取、结构动力响应的模态方法求解和结构辐射声功率的预估等具有一定的参考价值。

［1］郭骅， 姜哲.关于辐射效率的讨论 ［J］.振动工程学报，1992，5（2）：133－139.

［2］黎胜，赵德有.结构声辐射的振动模态分析和声辐射模态分析研究［J］.声学学报，2004，29（3）：200－208.

［3］EVERSTINE G C，HENDERSON F M.Coupled finite element／boundary element approach for fluid－structure interaction ［J］.Journal of the Acoustical Society of America，1990，87（5）：1938－1947.

［4］GIORDANO J A，KOOPMANN G H.State－space boundary element－finite element coupling for fluid－structure interaction analysis ［J］.Journal of the Acoustical Society of America 1995，98：363－372.

［5］CUNEFARE K A，ROSA S D.An improved state－space method for coupled fluid－structure interaction analysis［J］.Journal of the Acoustical Society of America 1999，105（1）：206－210.

［6］LI S.A state－space coupling method for fluid－structure interaction analysis of plates ［J］.Journal of the Acoustical Society of America，2005，118（2）：800－805.

［7］LI X H，LI S.Modal parameters estimation for fluid－loaded structures from reduced order models［J］.Journal of the A-coustical Society of America，2006，120：1996－2003.

［8］FAHY F.Sound and structural vibration： radiation， transmission and response［M］.London：Academic Press，1985.

［9］MCCOLLUM M D，SIDERS C M.Modal analysis of a structure in a compressible fluid using a finite element／boundary element approach ［J］.Journal of the Acoustical Society of America 1996，99（4）：1949－1957.

［10］BARRON R F.Industrial noise control and acoustics［M］.New York： Marcel Dekker Inc.， 2003.

［11］BERANEK L L.Noise and vibration control ［M］.New York： McGraw－Hill，1971.

Analysis of Structural Acoustic Radiation Loss Factor and Radiation Efficiency of a Plate Under Fluid Loading

Li Sheng1，2
1 State Key Laboratory of Structural Analysis for Industrial Equipment， Dalian University of Technology，Dalian 116024，China
2 School of Naval Architecture，Dalian University of Technology，Dalian 116024，China

The structural acoustic radiation loss factor and radiation efficiency of a plate under fluid loading were computerized and analyzed using finite element method and Rayleigh integral coupled method.The finite element method was employed for discretizing the structure.The Rayleigh integral was used for modeling the acoustic fluid.The modal acoustic radiation loss factor and the modal acoustic radiation efficiency were obtained with fluid－loaded undamped normal modes and reduced order models respectively.The numerical results of a plate in the air and in the water show that the acoustic radiation loss factor of an odd－odd mode is far larger than other types of modes， and the acoustic radiation loss factor in the air is about one order of magnitude lower than that in the water.The acoustic radiation loss factor in water is much bigger than the structural loss factor，and the acoustic radiation loss factor in the air is on the same order of magnitude of the structural loss factor.The acoustic radiation efficiency in air is about two orders of magnitude higher than that in water.

fluid loading effects；acoustic radiation； loss factor；radiation efficiency

TB532

A

1673－3185（2010）02－09－04

2009－09-01

辽宁省自然科学基金资助项目（20082170）；教育部留学回国人员科研启动基金资助项目

黎 胜（1973－），男，副教授，博士生导师。研究方向：船舶与海洋结构物振动噪声机理、预报及控制。E-mail：shengli＠ dlut.edu.cn