潜艇操纵性水动力数值计算中湍流模式的比较与运用

柏铁朝 梁中刚 周轶美 敬 军

中国舰船研究设计中心，湖北 武 汉 430064

潜艇操纵性水动力数值计算中湍流模式的比较与运用

柏铁朝 梁中刚 周轶美 敬 军

中国舰船研究设计中心，湖北 武 汉 430064

湍流模式的选取对潜艇操纵性水动力数值计算精度有着重要影响，采用六种湍流模式计算了SUBOFF主艇体及主艇体加指挥室围壳两种模型在一定漂角范围内的潜艇操纵性水动力，并与试验值进行了比较，结果表明SST k-ω模型更为适合潜艇操纵性水动力计算。在此基础上对SUBOFF全附体模型在一定漂角和攻角范围内的艇体水动力进行预报计算，并对该计算方法应用于潜艇操纵性水动力预报计算的计算精度与适用范围进行了探讨。

潜艇操纵性；水动力；湍流模式

1 引 言

潜艇操纵性是潜艇综合航行性能中非常关键的技术之一，良好的操纵性对于潜艇的战斗力、工作效能、安全性、经济性都有非常重要的意义［1］。潜艇操纵性研究的关键技术之一是确定水动力导数，而潜艇的水动力导数种类多达一百多项，有位置导数、角速度导数、舵角导数、以及复杂的耦合导数等。正是由于其复杂性，目前工程上还只能依赖缩比模型试验来获取潜艇水动力导数，但是这种方式显然存在一些缺点，比如：试验周期长、经费开支大、存在尺度效应和试验误差、原理性不强和受试验场地限制等。20世纪90年代以来，随着计算机技术的发展，运用CFD技术数值求解潜艇操纵性水动力与力矩成为可能并得到了运用［2－4］。潜艇操纵运动时外流场的典型特点是在翼面与主艇体的背流区域存在分离流现象且分离流随着来流攻角的增大更为明显。对于存在分离流的流场模拟，湍流模式是影响计算精度的关键因素之一。湍流模式的相关研究至今已经开展了100多年，可是目前仍然没有一种普遍适用的湍流模式，对于湍流模式的的分析评价一直是近几十年来流体力学的研究热点，即使是对已经存在并已获得广泛运用的湍流模式也缺乏公认的评价［5，6］。很多情况下，湍流模型的选取要考虑到研究者经验、流场流动的特点、计算精度与计算能力后方可决定。

为比较目前在CFD计算中获得广泛运用的5种二方程湍流模式及RSM湍流模式对潜艇操纵性运动时绕流场模拟的准确性，本文首先采用这些模式对SUBOFF两种简单模型在一定漂角范围内的水动力与力矩进行计算，将计算值与实验值进行比较，得出了更适用于潜艇操纵性水动力数值计算的湍流模型。在此基础上计算了全附体SUBOFF潜艇模型在一定攻角和漂角下的水动力与力矩，并讨论了该数值计算方法用于潜艇操纵性水动力预报的计算精度与适用范围。

2 湍流模型的比较与选取

在进行分析计算时，将相关参考及坐标定义为：L——主艇体长；Lpp——艇体垂线间长；LF——艇体进流段长；Lp——艇体平行中体长；LA——艇体去流段长；D——艇体最大直径；xcg——艇体重心至艇艏距；H——指挥室围壳高；LS——指挥室围壳长；B——指挥室围壳最大宽度；Ls－f——指挥室围壳前缘至艇艏距离；l——尾翼展长；bb——尾翼底部弦长；bt——尾翼端面弦长；lf－f——尾翼后缘至艇艏距离；U——来流速度；X——纵向力；Y——横向力；Z——垂向力；K——横倾力矩；M——纵倾力矩；N——转艏力矩

文中设定纵舯剖面与基面的交线为x轴 （横坐标），向艇艉为正方向；舯截面与基面的交线为y轴 （纵坐标）；纵中剖面与舯截面的交线为z轴（竖坐标），向上为正方向，向右舷为正方向。原点为艇艏端点。

2.1 计算模型的选取

本文选用SUBOFF主艇体（图1）和SUBOFF主艇体加指挥室围壳（图2）两种模型作为计算对象，其原因有以下两点：其一，潜艇操纵运动时，作用在主艇体上的水动力是潜艇总水动力的主要组成部分，且主艇体的绕流场是典型的三维分离流动，所以主艇体水动力计算的准确度将直接影响到全附体潜艇水动力的计算精度；其二，主艇体加指挥室围壳模型是典型的潜艇主／附体连接形式，对研究潜艇操纵性水动力数值计算方法具有直接的指导意义。模型的主要参数如表1所示。

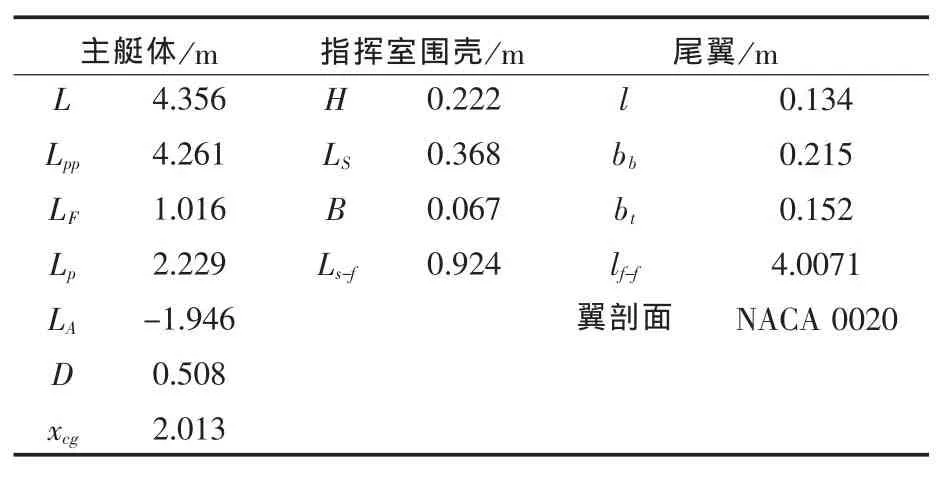
表1 SUBOFF模型主要参数

2.2 计算流域、网格划分及边界条件设定

2.2.1 计算流域

计算流域为一长方体区域（图3），L为艇体长度，其边界范围为：

2.2.2 网格划分

采用ICEM CFD软件划分网格，为提高计算精度整个流域采用全结构网格布置。其中，主艇体与主艇体加指挥室围壳模型的网格数分别为114万和162万。

2.2.3 边界条件设定

1） 进口处为速度进口边界条件，u＝3.341 m／s，入口处湍流参数根据相关文献［7］给定。

2）出口为压力出口边界条件。

3）上下面为对称边界条件。

4）艇体表面为壁面无滑移边界条件。

5）k－ε与RSM模型在近壁区采用壁面函数法，k－ω模型采用近壁模拟法。

2.3 湍流模式与数值计算方法

文中对二方程湍流模式中的Standard k－ε模式、RNG k－ε 模式、Realizable k－ε 模式、Standard k－ω模式、SST k－ω模式及RSM湍流模式进行分析比较，各湍流模式的数学表达及特点可参照相关文献［6］，［7］。计算采用直接求解三维粘性不可压RANS方程的方法，使用有限体积法对微分方程进行离散，扩散项使用中心差分格式，对流项采用二阶迎风格式，流场计算采用SIMPLEC算法。

2.4 计算结果及分析

运用FLUENT软件求解流场，得到在漂角β⊂（0°～18°）范围内主艇体模型横向力系数 Y′、转艏力矩系数N′（图4～5）与主艇体加指挥室模型的横向力系数Y′、垂向力系数Z′及转艏力矩系数N′（图6～ 图 9），并将其与文献［8］中的试验结果比较。

计算结果表明：在小角度范围内（β≤10°）文中运用的6种湍流模式计算得到的水动力与力矩与试验值均非常接近。随着漂角的继续增大，计算值的误差均随之增大，且不同湍流模式的精度亦有较大差别（表2～表3）。其中，运用RSM与k－ω模式得到的结果与试验值更为接近，而Standard k－ε模式的误差相对较大。其原因主要有：

1）随着漂角增大分离流的强度也在加强，RANS湍流模式均不能很好地处理大攻角下的分离流计算。

2）湍流模型对计算结果有着重要影响，主要体现在Reynolds应力项的处理方式及各模型在近壁区的处理方法。

对于Reynolds应力项的处理，k－ε与k－ω模型均基于Boussinesq粘涡假定，属于各向同性湍流模式，但在近壁湍流及弯曲壁面流动中的雷诺应力具有明显的各向异性。而RSM模型是基于雷诺应力转化模型，考虑了一些各向异性效应，所以计算精度应优于二方程模型。

对于近壁区的处理方法，在FLUENT软件中主要有壁面函数法及近壁模拟法。k－ε模式与RSM模式属于高Re数的湍流计算模型，而近壁区的流动仍属于低Re数流动，所以其近壁处理通常借助于壁面函数，但壁面函数法的表达式主要根据简单的平行流边界层的实测资料归纳得出，不能“真实”地反映近壁区内流动状态，而且当流动为弯曲壁面流动或流动分离过大时，这种处理方法不太理想［9］。 而k－ω 模式在近壁处采用Wilcox k－ω近壁模拟，考虑了低Re数效应，能准确地模拟近壁区的流动状况，且具有较好的数值稳定性。需要指出的是Wilcox k－ω近壁模拟模型对近壁区的网格稠密度要求较高。由于操纵性计算中关注的力与力矩的计算精度主要与近壁区内压力计算精度有关。从这个角度来看，k－ω模式的计算精度要优于k－ε、RSM模式。

为进一步开展分析，本文比较了漂角β＝18°状态下的几种模式的计算差异。比较图4～图8可知，指挥室围壳对潜艇操纵性水动力性能影响显著，以β＝18°状态下转艏力矩系数N′作为分析对象，针对靠近主艇体的一个指挥室围壳剖面（Z＝－0.27 m），比较了运用 RSM、SST k－ω 与 Standard k－ε湍流模式的计算压力分布。在指挥室围壳迎流面三种湍流模式的计算结果非常一致，如图9～图10所示。在背流面出现较大范围的分离流（图11）时，采用RSM、SST k－ω模式计算出的表压分布一致，而Standard k－ε模式与二者有较大差别，主要是在分离区域内压力值低于运用RSM、SST k－ω模式得到的压力值，这是运用Standard k－ε模式计算得到的N′值偏大的原因之一。

综合以上分析可知：在小漂角范围内，针对这两种计算模型，文中运用的二方程湍流模式与RSM模型均有较高的计算精度，在较大漂角下，RSM模式、k－ω模式的计算精度要优于k－ε模式，其中Standard k－ε模式误差较大，而改进后的RNG k－ε、Realizable k－ε模式在计算精度与数值稳定性上均优于Standard k－ε模式。值得注意的是，RSM模式虽然考虑了一些各项异性效应，但本文的计算表明，在潜艇模型处于较大的来流攻角下并没有显出其明显的数值稳定性与计算精度优势，且RSM模式的计算时间要比二方程模型多耗费40%左右。而SST k－ω模式在近壁处采用Wilcox k－ω近壁模拟，在边界层边缘和自由剪切层采用k－ε模式的k－ω形式，其间通过一个混合函数来过渡，这样消除了k－ω模式的原型对自由来流湍流度的极强依赖性，使其对自由来流的湍流度也不敏感。本文计算亦表明宜采用SST kω模式做为潜艇操纵性水动力数值计算的湍流模式。

表2 主艇体模型横向力系数、转艏力矩系数计算结果

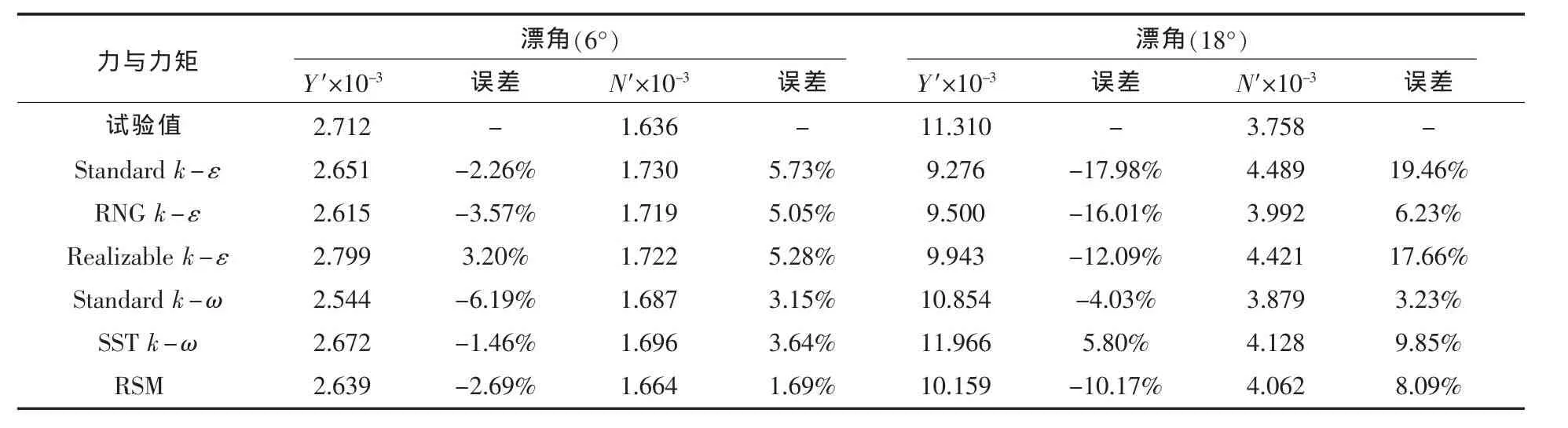
表3 主艇体加指挥室围壳模型横向力系数、转艏力矩系数计算结果

3 全附体潜艇模型操纵性绕流场数值计算

前面针对主艇体及主艇体加指挥室围壳模型的操纵性水动力性能进行了计算，计算结果与试验值较吻合。为进一步探究该方法对潜艇操纵性水动力的预报能力，作者针对SUBOFF全附体模型（图 12）在较大攻角 α⊂（－16°～16°）和漂角 β⊂（0°～14°）范围内的潜艇操纵性水动力性能进行了计算。如图13～图20所示，计算结果表明：

1） 在攻角 α ⊂（－16°～16°） 内， Realizable kε、SST k－ω两种湍流模式的计算值与试验值的比较符合预期规律，其中SST k－ω模式的计算值更为接近试验值。在小攻角（≤10°）范围内计算值与试验值非常接近（误差在7%以内）。

2） 在漂角 β⊂（0°～14°）内，采用 SST k－ω 模式的计算结果基本与试验值一致，但相对于模型在有攻角下的计算结果误差较大。其重要原因在于处于斜流之中的指挥室围壳对操纵性水动力有很大影响，而由此引发的背流区流动分离及主附体间的干扰作用对数值计算精度有着不小的挑战。需要指出的是，在漂角β＝0°时，文中引用的水池试验数据中K′、N′、Z′值均与零点有较大差别，这表明试验数据本身也存在一定的误差，但比较试验水动力导数与通过线形回归 β⊂（0°～4°）内的计算值所得的水动力导数可知两者基本一致，如表4所示，这也表明了数值计算运用于求解潜艇操纵性水动力系数的准确性。

3） 考虑到模型在有攻角 α⊂（－16°～16°）的其余4个分力变化均不明显，限于篇幅本文未列出。对比本文3个模型在攻角与漂角下的计算结果可知：指挥室围壳对水平面潜艇操纵性能有着至关重要的影响，潜艇回转过程中伴随的横倾、纵倾和潜浮运动均与指挥室围壳的外型与位置有着紧密的联系，因此基于潜艇操纵性考虑的艇体指挥室围壳外型优化的是非常必要的。

4）随着攻角和漂角角度的增加，计算值误差增大较为明显，与工程许可的误差限定亦有较大差距。影响大角度下计算精度的关键还是在于各种湍流计算模式对流动分离的模拟能力。对于存在大规模的分离湍流流场，RANS模型的计算精度有限。

表 4 中，Yν′， Kν′，Nν′试验值为试验报告直接给出，而水动力导数的计算值及 Zν′，Mν′试验值为作者通过最小二乘法线性回归 β⊂（0°～4°）时计算数据与试验数据所得。

表4 水动力导数对照表

4 结 论

本文详细比较了6种RANS湍流模式对SUBOFF主艇体及主艇体加指挥室围壳模型的操纵性水动力计算精度的影响，得出了较为适合潜艇操纵性水动力计算的湍流模式，在此基础上对全附体SUBOFF模型在有攻角和漂角下的六分力进行了计算，并对该计算方法运用于潜艇操纵性水动力预报计算的计算精度与适用范围进行了有益的探讨，初步讨论了指挥室围壳对潜艇操纵性能的影响。主要结论如下：

1）对于潜艇操纵性水动力数值计算，k－ω模式及RSM模式的计算精度要优于k－ε模式，其中运用Standard k－ε模式得到的计算误差较大。考虑到计算精度与计算时间，SST k－ω湍流模型更为适合进行潜艇操纵性水动力数值计算。当然，必须要注意的是k－ω采用的近壁模拟方法对近壁区网格稠密度要求比壁面函数法要高。

3）计算表明指挥室围壳对潜艇水平面的操纵性能影响较大，在潜艇水平面变漂角过程中，艇体所受的垂向力、横滚力矩及俯仰力矩均有较大变化，这些力与力矩对潜艇转向和回转过程中的艇体姿态控制非常重要。因此，开展基于潜艇操纵性能考虑潜艇指挥室围壳外型优化的研究非常必要。

［1］陈厚泰.潜艇操纵性［M］.北京：国防工业出版社，1981.

［2］TAYLOR L K，PANKAJAKSHAN R M，JIANG C S.Large-scale simulations for maneuvering submarines and propulsors ［C］//AIAA 29th Plasmadynamics and Lasers Conference， 1998.AIAA.98-2930.

［3］ZHENG X，LIAO C，LIU C.Multigrid multi-block computation of incompressible flows using two-equation turbulent models ［C］//AIAA 35th Aerospace Sciences Meeting and Exhibit，1997.AIAA.97-0626.

［4］潘子英，吴宝山，沈泓萃.CFD在潜艇操纵性水动力工程预报中的应用研究［J］.船舶力学，2004，8（5）：42-51.

［5］WILCOX D C， LA CÄNADA.Turbulence modeling： an overview［C］//AIAA 39th Aerospace Sciences Meeting and Exhibit， 2001.AIAA.2001-0724.

［6］张兆顺，崔桂香，许春晓，等.湍流理论与模拟［M］.北京：清华大学出版社，2005.

［7］Fluent Inc.FLUENT User’s Guide［S］.Fluent Inc.2003

［8］RODDY R F.Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model［R］.Departmental Report，Ship Hydromechanics Department，David Taylor Research Center，1990.

［9］王福军.计算流体动力学分析［M］.北京：清华大学出版社，2004.

Comparison and Application of Turbulence Modes in Submarine Maneuvering Hydrodynamic Forces Computation

Bai Tie－chao Liang Zhong－gang Zhou Yi－mei Jing Jun
China Ship Development and Design Center，Wuhan 430064，China

The selection of turbulence mode plays an important role in the accurate numerical simulation of a submarine maneuvering hydrodynamic forces.In this paper，computations with six different turbulence modes were performed for the two configurations of the SUBOFF model，one was an axisymmetric hull and the other was hull with sail.Compared with experimental data，the results for varying drift angles，indicate that SST k－ω turbulence model is more suitable for submarine maneuvering hydrodynamic forces computation.Then，computation and prediction of the maneuvering hydrodynamic forces for SUBOFF model with full appendages were processed by varying attack angles and drift angles.The accuracy and applicability of the present method for predictive computation of submarine maneuvering hydrodynamic forces were also discussed.

submarine maneuverability； hydrodynamic force； turbulence mode

U661.1

A

1673－3185（2010）02－22－07

2009－05－06

柏铁朝（1984－），男，硕士研究生。研究方向：船舶水动力数值计算研究。E-mail：baitiechao＠qq.com

梁中刚（1966－），男，研究员，硕士生导师。研究方向：船舶总体研究设计