Discrete Stress-strength Interference Model of Reliability Analysis under Multi-operating Conditions

AN Zongwen , HUANG Hongzhong, *, WANG Zhonglai, ZHANG Xiaoling, and WANG Guibao

1 School of Mechatronics Engineering, Lanzhou University of Technology, Lanzhou 730050, China

2 School of Mechatronics Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

1 Introduction

The stress-strength interference (SSI) model has been widely used for reliability analysis of mechanical components. In this model, the component reliability denoted by R can be defined as

where S and C represent the stress on a component and the strength of the component, respectively.

In further investigations concerning the SSI model, it has become an important research topic to calculate component reliability based on the probability distributions of both stress and strength. Therefore, efforts have been made by many researchers. KAPUR[1]devised an approach for determining the bounds on the exact unreliability, and this approach requires only information regarding the subinterval probabilities within an interference region. To improve its accuracy of calculation, PARK, et al[2],modified KAPUR’s formulation on the quadratic programming problem and presented a solution to this problem. SHEN[3]proposed another empirical approach to calculate the unreliability bounds based upon the subinterval probabilities of both stress and strength in the interference region. WANG, et al[4], presented a multiple-line-segment method of implementing the SSI model when only discrete interval probabilities of both stress and strength inside an interference region are available. GUO, et al[5], presented an algorithm for computing the unreliability bounds based on an improved Monte Carlo method. WANG, et al[6], presented an approach to calculate fuzzy unreliability of a component/system, and in this approach, the probability density functions of both stress and strength are approximated by piecewise fuzzy line-segments that were expressed by linear fuzzy polynomials, and the discrete interval probabilities were treated as fuzzy numbers. KOTZ,et al[7], gave a comprehensive survey of the SSI models presented in the literature before 2002, and some associated recent results. Recently, on the basis of universal generating function(UGF), AN, et al[8], presented a discrete SSI model,which can be used to determine the component reliability when both stress and strength are discrete random variables(RVs).

In the models or methods discussed earlier, the stress acted on a component is usually represented by a single RV.But under multi-operating conditions, a single RV can not reflect the actual stress state of a component. For instance,during the taking-off, cruising and landing phrases of an aircraft, the working stress of a part in the transmission system has different statistical characteristics (for example,mean values of stress). In this case, a more natural method is to employ multiple different RVs to describe the stress characteristics of the part under different working phases.Therefore, in this paper, multiple discrete RVs are defined based on the actual range of component stress firstly, which are used to represent the multi-operating conditions of the component. Then the component reliability under each operating condition is calculated, respectively.

The rest of this paper is organized as follows. Section 2 gives a brief description of UGF method and the discrete SSI model. Section 3 formulates a generalized problem and builds the discrete SSI model under multi-operating conditions. For demonstrating the validity of the model,section 4 provides an illustrative example. The conclusions are summarized in section 5.

2 UGF Method and Discrete SSI Model

2.1 UGF method

The concept of UGF was introduced by USHAKOV[9].In a series of research work by LISIANSKI and LEVITIN[10,11], the UGF method has been applied to reliability analysis and optimization of multi-state systems.

Suppose that a discrete RV X has a probability mass function(PMF) characterized by two vectors x and p, which consist of the possible values and corresponding probabilities of X, respectively. We can rewrite them as follows:

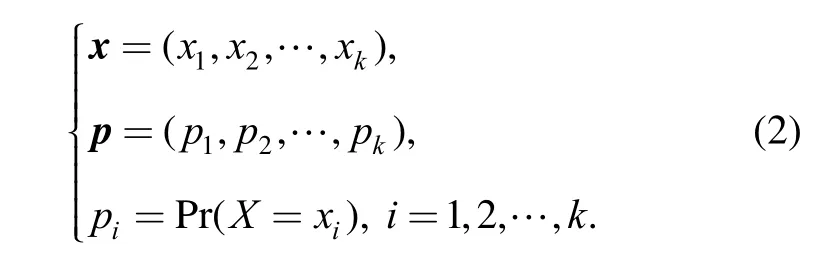
Based on the basic principle of UGF method, the PMF of discrete RV X can be represented by a polynomial function of variable z,, that relates the possible values of X to the corresponding probabilities:

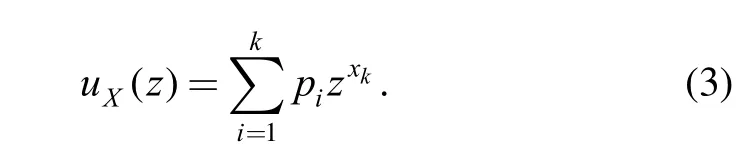
Consider n independent discreteand an arbitrary function of these variablesSuppose that the numbers of possible values of these RVs are, respectively. According to Eq. (3), the UGFs of the individual RVs can be obtained as follows:

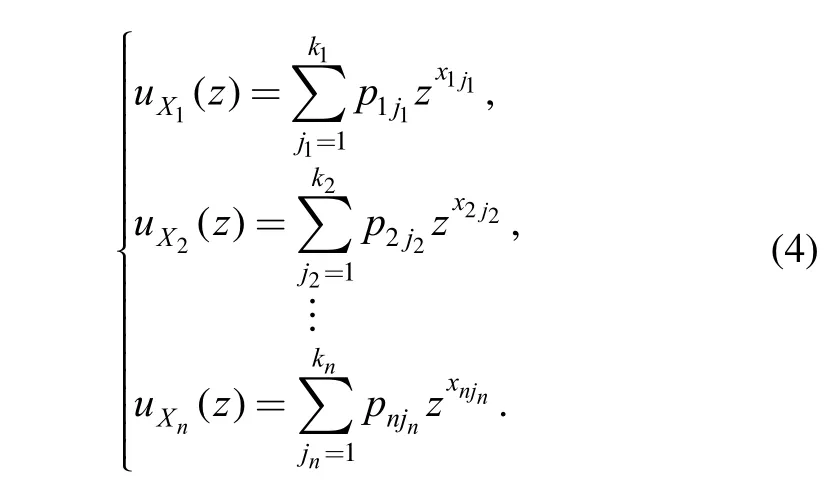
Then, by employing the composition operator ⊗, the UGF of functioncan be obtained as

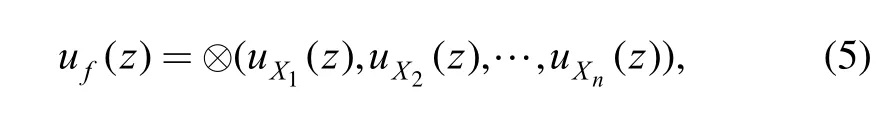
where the composition operator ⊗is defined as

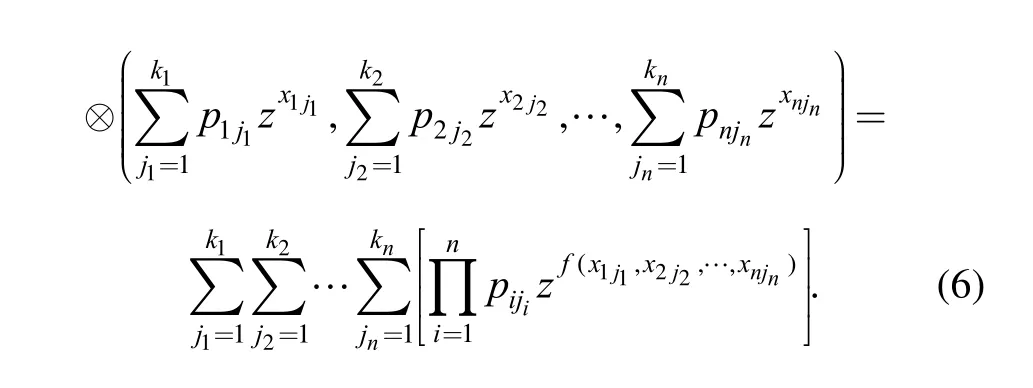
Indeed, the composition operator ⊗represents an operation rule which strictly depends on the expression of functionIn the procedure of operation,the coefficients of each term of a polynomial are multiplied and the exponents exactly correspond to the definition of function

2.2 Discrete SSI model

The discrete SSI model was established based on UGF method[8]. Its basic idea is to treat stress and strength as two independent discrete RVs. Suppose that the PMF of stress S and that of strength C are known as follows:

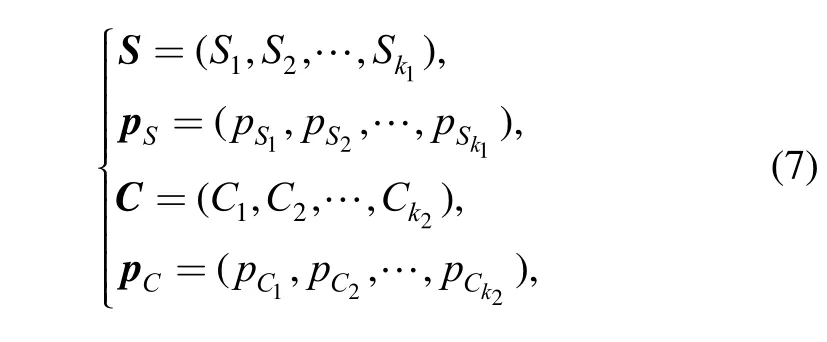
where k1and k2are numbers of possible values that S and C can take on, respectively. According to Eq. (3), the UGF of stress and that of strength can be obtained, respectively, as follows:

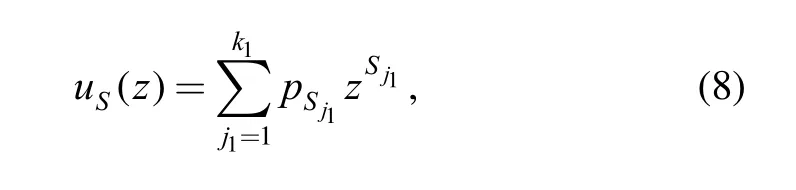
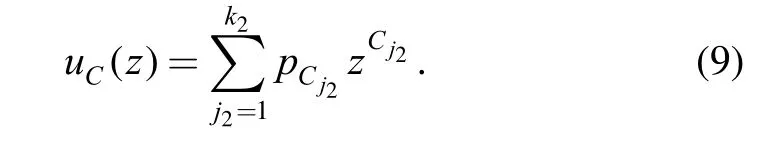
Then, define a function f ( S , C) of stress and strength as

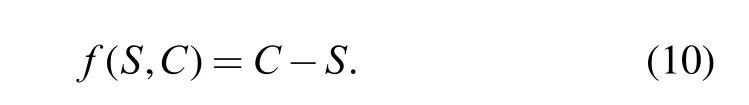
The UGF of f ( S , C) can be obtained according to Eqs. (5)and (6). Its final form is also a polynomial function containingterms (the total number of terms can be less than k1×k2after collecting like terms):

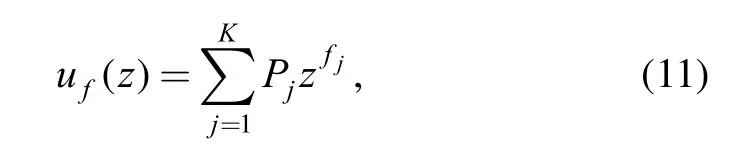
where fjandare possible values of function f ( S , C) and the corresponding probabilities,respectively.

Using Eq. (10), the component reliability given in Eq. (1)can be further expressed as

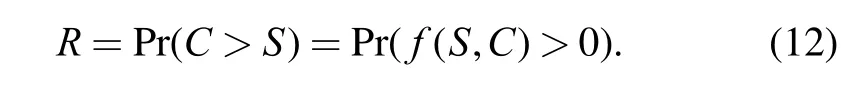
To obtain the probability in Eq. (12), the coefficients of polynomial uf(z )expressed by Eq. (11) can be summed for every term with fj＞0. For the sake of depiction, we can define a binary-valued function α(fj) with domain on the set of possible values of function f ( S , C) as

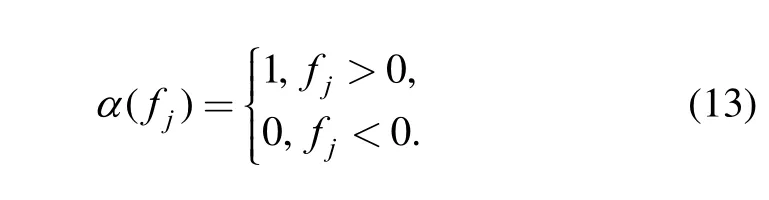
Then, Eq. (12) can be rewritten as

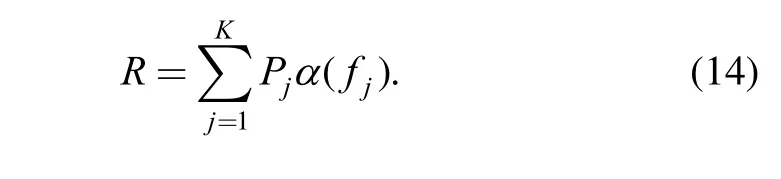
Eq. (14) is called the discrete SSI model.

3 Discrete SSI Model under Multi-operating Conditions

In this section, a generalized problem is formulated, after which the discrete SSI model under multi-operating conditions is constituted.

3.1 Formulation of the problem

In practical engineering, components are designed to perform their intended tasks in a given environment. In some cases, because of the random variation in magnitude and random occurrence of an external load, it is not appropriate to describe stress of a component as a single RV. But at least, we can estimate the range of stress.Without loss of generality, suppose that the service stress of a component vary from Sminto Smax, which depends on the change of external loads. In this case, we can naturally think that the component can perform its tasks under various stress conditions, and that it has different reliabilities under different stress conditions.

Generally speaking, the stress state of a component can be categorized based on the characteristic of external loads.For instance, the stress state of a mechanical component can be simply classified as state 1, state 2 and state 3,which correspond to low load, moderate load and heavy load, respectively. More generally, according to the change of external loads, the stress of a component can be categorized into arbitrary finite state: state 1, state 2,…,state m.

The actual stress on the component can be an arbitrary value within the interval of. This interval can be approximately treated as a finite set of stress values,which can be regarded as all possible stress values of the component. A stress state of the component can be represented by a correspondence between all possible stress values and their occurrence probabilities. Each stress state is characterized by a discrete RV with specific PMF. We can assume that a number of possible values of stress are identical for any stress state and that different states differ by probabilistic distribution of the possible values.ith stress state,the possible values of siis avector siand the

If a discrete RV si( i = 1,2, … ,m)is used to denote the corresponding probabilities is another vector ip. Then the PMF of sican be written as follows:

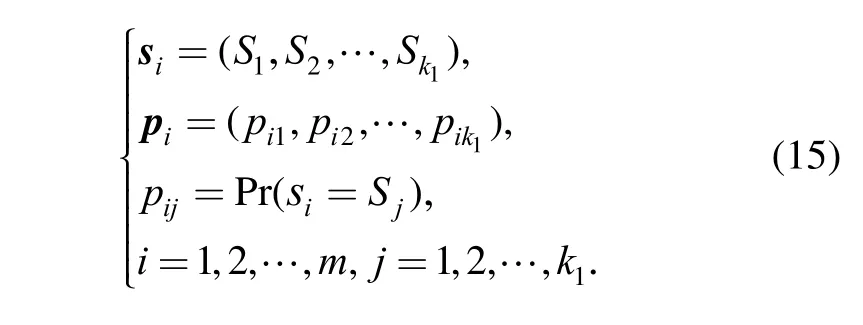
By doing so, we can obtain all PMFs of m discrete RVs that represent m different stress states. If the strength of the component is given, the final problem can be generalized to determine the reliabilities of the component under m stress states. To solve this problem, we can use the discrete SSI model introduced in section 2.

3.2 Solution to the problem

For the sake of simplicity, we suppose that the strength of the component is also a discrete RV with k2possible values. (When the strength is a continuous RV, it can be approximated by a discrete RV, see section 4.). When the PMFs of stress state siand strength C are known as follows:and the functionis defined as

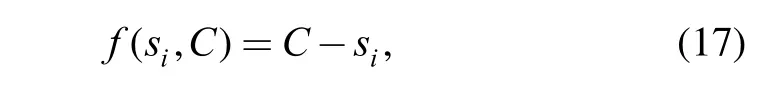
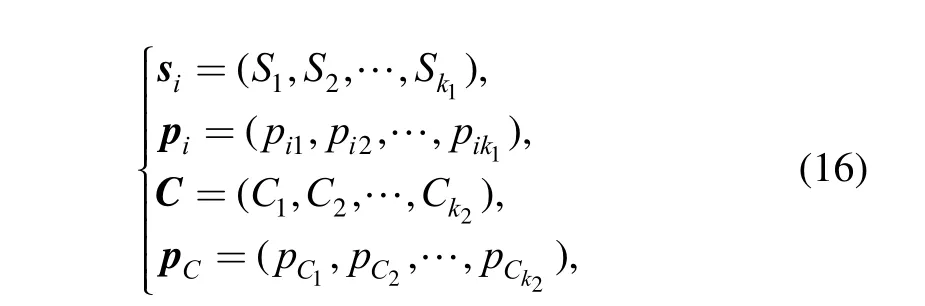
the component reliability under the ith stress state denoted by Rican be obtained according to Eq. (14) as

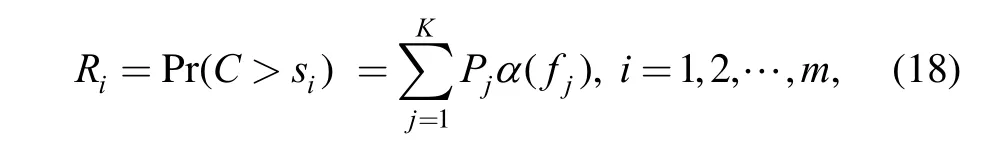
where fjand Pj(j=1, 2,…, K) are possible values of function f ( si, C ) and the corresponding probabilities,respectively.

Using this method, we can get m values of the component reliability, which correspond to m operating conditions of the component. Therefore, Eq. (18) can be called the discrete SSI model under multi-operating conditions.

4 Illustrative Example

Loading situations of a transmission component of the decelerator installed in an aeroengine are very complex during taking-off, cruising and landing phases of an aircraft.Suppose that the random external loads cause stress on the component in the range of 0–100 MPa and the strength of the component is normally distributed with mean μC= 100 MPa and standard deviation σC= 10 MPa.

To evaluate the component reliability using Eq. (18), we will approximate the continuous RV of strength with a discrete RV. Based on engineering experience, we can determine an approximate range of strength, which can be denoted by the interval of. Then, this interval can be divided into finite subintervals. The midpoint values of each subinterval are treated as possible values of strength and the area values of each subinterval are treated as the corresponding probabilities. Thus, we can obtain a discrete RV of strength with known PMF. In this example,the interval ofis determined asMPa and it is divided into six subintervals. Accordingly, the strength of the component can be expressed by a discrete RV with PMF expressed by Eq. (19):

Similarly, the range of stress, 0–100 MPa, can be divided into five subintervals, and the midpoint values of the subintervals are regarded as possible values of stress. Then,we can define multiple stress states by assigning different probability values to these possible values of stress. In this example, we define three stress states: state 1, state 2 and state 3, which represent the stress characteristic of the component during taking-off, cruising and landing phases of the aircraft, respectively. Thus, we can obtain PMFs of three discrete RVs of stress state, s1, s2and s3, which can be expressed as follows:

Now, the working situation of the component is approximately represented by three pairs of combinations of stress and strength, (s1, C), (s2, C) and (s3, C), which are depicted in Fig.

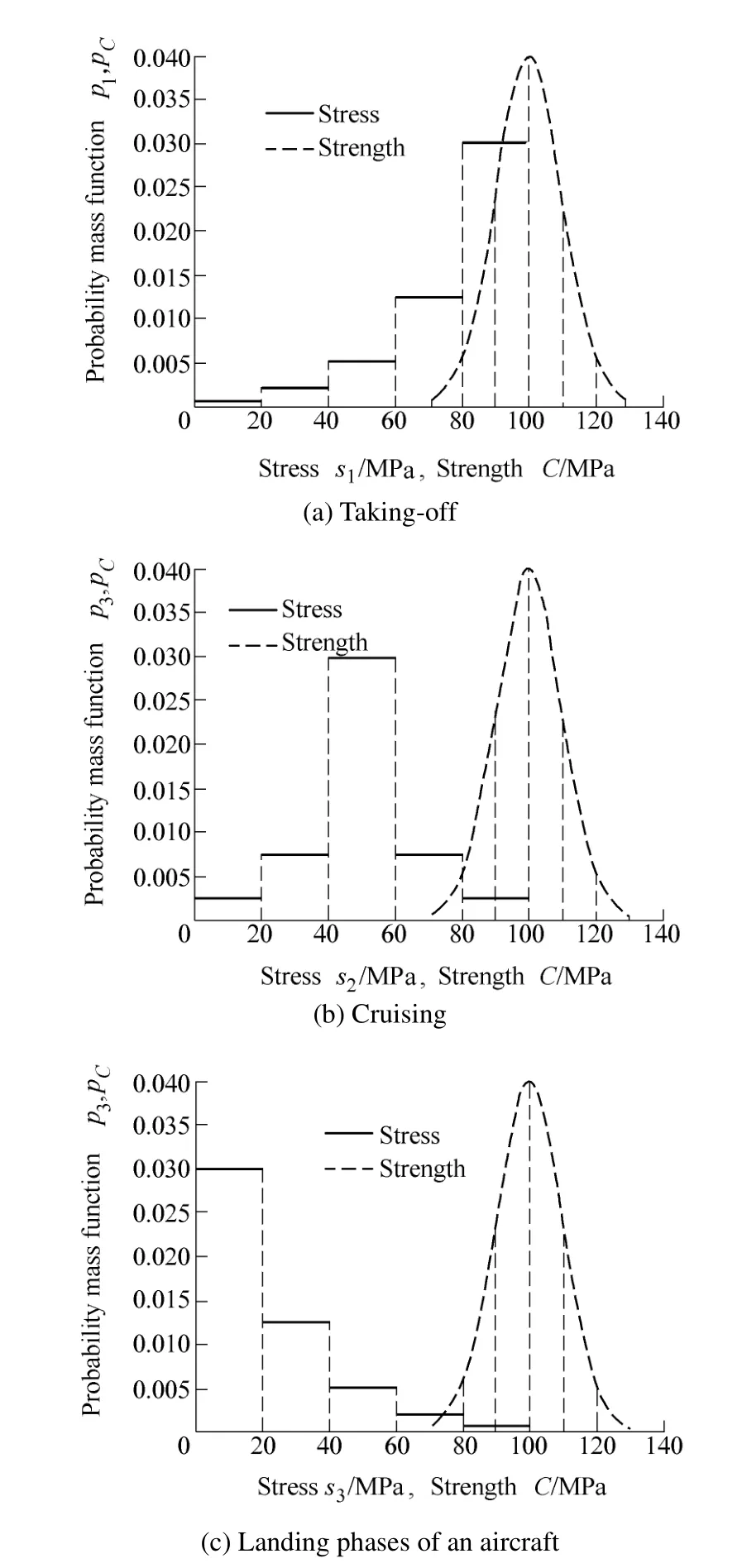
Fig. Working situation of the component during different courses

In state 1, according to Eq. (2), we can obtain the UGFs of s1and C as follows:

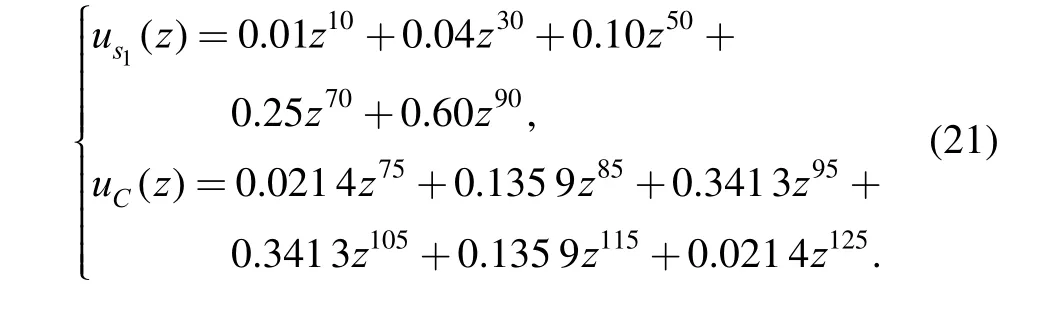
According to Eqs. (5) and (6), the UGF of functioncan be obtained as

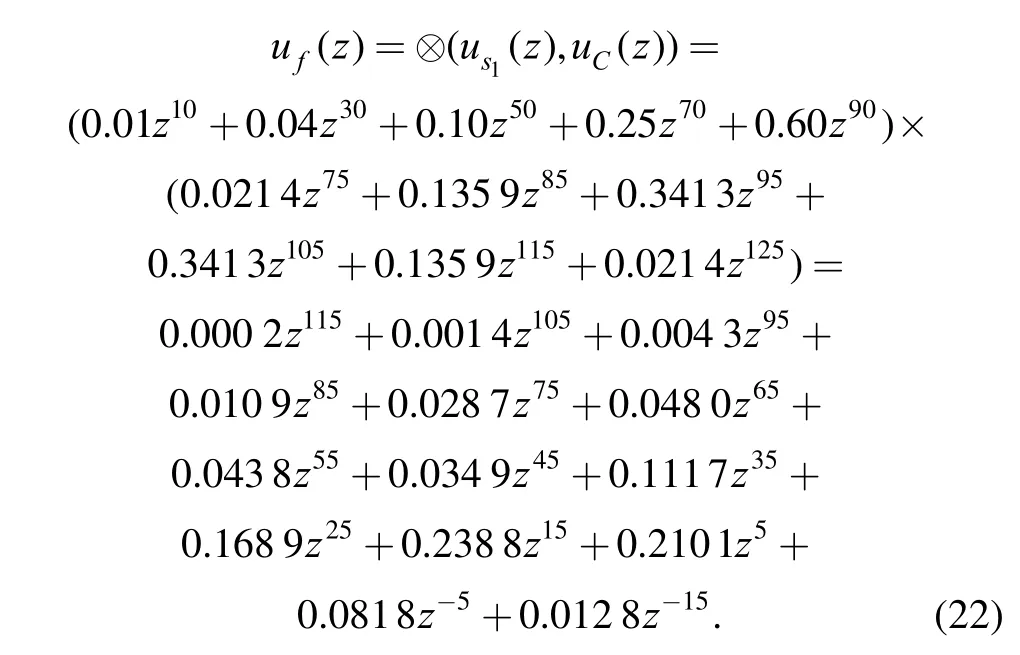
It can be seen that the UGF of function f (1s , C)contains above fourteen terms after collecting like terms.According to Eq. (18), the component reliability in state 1 can be calculated as

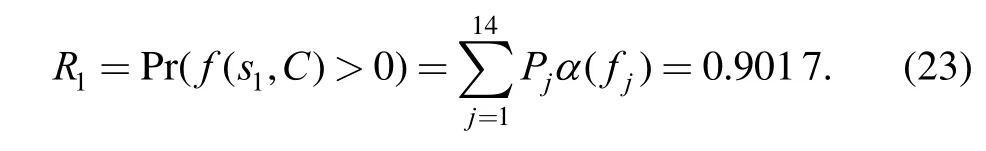
In the similar way, we can get the reliabilities of this component in state 2 and state 3, respectively:

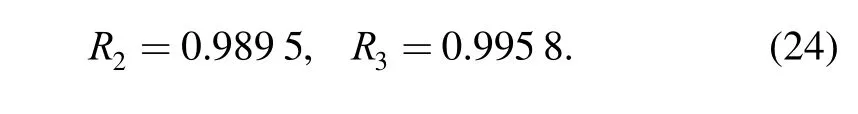
The above results indicate that the reliability values of this component are equal to 0.901 7, 0.989 5 and 0.995 8 during taking-off, cruising and landing phases, respectively.

5 Conclusions

(1) According to the actual stress range, multiple discrete RVs are constituted, which are used to represent the multi-operating conditions of the component.

(2) The component reliabilities under different operating conditions are calculated, one by one, by employing the discrete SSI model and UGF technique.

(3) The discrete SSI model under multi-operating conditions is presented and its effectiveness is demonstrated by an illustrative example. With this model,the application range of the conventional SSI model can be extended.

[1] KAPUR K C. Reliability bounds in probabilistic design[J]. IEEE Transactions on Reliability, 1975, R–24(3): 193–195.

[2] PARK J W, CLARK G M. Computational algorithm for reliability bounds in probabilistic design[J]. IEEE Transactions on Reliability,1986, R–35(1): 30–31.

[3] SHEN K. An empirical approach to obtaining bounds on the failure probability through stress/strength interference[J]. Reliability Engineering and System Safety, 1992, 36(1): 79–84.

[4] WANG J D, LIU T S. A discrete stress-strength interference model for unreliability bounds[J]. Reliability Engineering and System Safety, 1994, 44(2): 125–130.

[5] GUO Song, LIU Tianyi. Reliability bounds determined by improved Monte Carlo method for stress-strength interference system[J].Chinese Journal of Mechanical Engineering, 1994, 33(3): 93–98.(in Chinese)

[6] WANG J D, LIU T S. Fuzzy reliability using a discrete stress-strength interference model[J]. IEEE Transactions on Reliability, 1996, 45(1): 145–149.

[7] KOTZ S, LUMELSKII Y, PENSKY M. The stress-strength model and its generalizations. Theory and applications[M]. Singapore:World Scientific, 2003.

[8] AN Zongwen, HUANG Hongzhong, LIU Yu. A discrete stress-strength interference model based on universal generating function[J]. Reliability Engineering and System Safety, 2008, 93(10):1 485–1 490.

[9] USHAKOV I. A universal generating function[J]. Soviet Journal of Computer and Systems Sciences, 1986, 24(5): 118–129.

[10] LISNIANSKI A, LEVITIN G. Multi-state system reliability.Assessment, optimization and applications[M]. Singapore: World Scientific, 2003.

[11] LEVITIN G. The universal generating function in reliability analysis and optimization[M]. London: Springer, 2005.