非线性系统的多项式近似表示及电力系统应用（Ⅱ）——应用篇

孙玉娇， 刘锋， 梅生伟

（清华大学电机系电力系统国家重点实验室，北京 100084）

0 引言

在电力系统暂态稳定分析方法中，时域仿真法受系统规模及计算速度的限制，难以提供定量分析的相关信息;而直接法则可避免大量的积分过程，可利用系统的自身结构及动态特性来分析电力系统暂态稳定性，但其缺点是受系统模型的限制。

直接法中存在两个关键性问题:一是平衡点求取;二是稳定域边界近似。其中，平衡点求取是直接法中的关键，目前虽然已提出多种方法［1－10］，但却仍是一个未能解决的难题，主要原因在于:1）电力系统中平衡点个数为无限个;2）无法确定电力系统暂态稳定域边界上平衡点个数及分布情况。

为克服平衡点求解的困难，文献［11］提出了利用多项式近似系统研究电力系统平衡点及其稳定域边界近似的方法，并在理论上证明了该方法的合理性。本文结合多项式系统平衡点求解的优势及电力系统自身的特点，利用多项式近似系统研究原系统的平衡点及稳定域边界近似，并以一个单机无穷大系统及一个三机系统为例，验证了所提方法的有效性。下面将分别介绍电力系统模型的多项式近似表示及多项式近似系统与原系统的关系，最后给出算例结果并得出结论。

1 电力系统模型的多项式近似表示

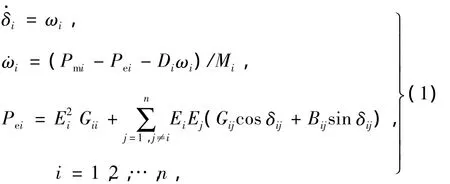
考虑一般的经典n机电力系统非线性模型对上述系统，在稳定平衡点（SEP）处进行s阶Taylor展开，利用半张量积［12］方法，可得近似系统

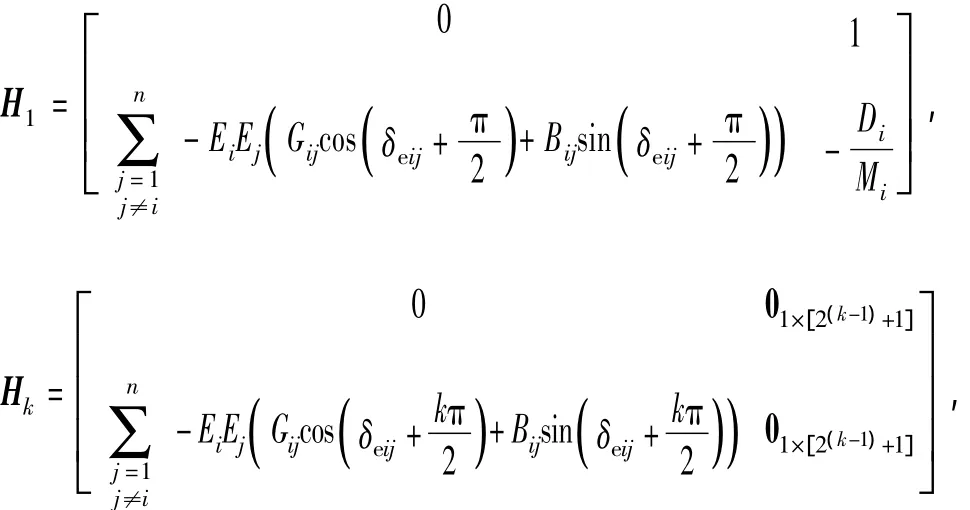
式中:H1为系统（1）在SEP处的一阶导数，即传统的Jacobi矩阵;Hk是系统（1）在 SEP处的k阶导数，为2×2k维的二维矩阵，即式中:δeij= δei－ δej;01×2（k－1）表示 1 ×2（k－1）维且元素均为0的矩阵，称其为0矩阵，是为文章表述方便而简写。本文其余用到0矩阵的地方，意义与此相同，不再作解释。

可以看出，高维系统高阶导数利用半张量积方法可进行方便的表达与操作，因此可克服传统方法中对高维高阶导数表达及操作困难的缺点。

由电力系统自身的特点及文献［11］所述多项式近似系统与原非线性系统的关系可知电力系统模型的多项式近似系统有如下特点:a）在较大范围内可保证良好的近似精度。通常Taylor展开的范围局限为展开点（或平衡点）的一个邻域，但电力系统模型主要包含正弦及余弦函数，对此类函数多项式可在较大范围内实现很好的近似;b）在足够高的近似阶数下，多项式近似系统平衡点与原系统平衡点可任意接近［11］;c）在足够高的近似阶数下，多项式近似系统平衡点与原系统相应平衡点类型可保持一致［11］。

2 多项式近似系统平衡点的求解

目前，电力系统暂态稳定分析中平衡点的求取是一个难点，其主要原因在于稳定域边界上平衡点总数及分布情况未知。而多项式系统则可在一定程度上减弱这一困难。原因如下:a）根据代数几何理论，多项式系统实根个数或其上界可确定［13－14］;b）目前多项式求解算法已有深入研究，对于某些多项式系统存在有效方法求出其全部实根。多项式系统求解方法可分为代数方法及数值方法，二者均可求出多项式系统的全部根，但代数方法计算量大，不适用于大系统，而数值方法中的同伦法［15－16］（或称连续法）则因其强大的理论基础及计算优势得到认同。最初同伦法路径数由多项式系统根的最大个数——Bezout数决定，即由多项式系统中各多项式的最高阶数之积决定，但实际系统中根的个数通常远小于Bezout数，由此导致同伦法中大量路径发散，引起不必要的计算支出，文献［16］采用齐次化方法减少同伦路径数从而提高计算速度并通过确定求解多项式系统全部根所需的最大路径数来避免盲目求解，由此克服已有同伦法的不足。此外，同伦法目前已在并行计算中实现并可解决实际中较大系统的求解问题［17］。

由此可见，多项式近似系统由于其结构的特殊性，可以在平衡点求解上具有一定的优势;而文献［11］已经证明当近似阶数足够高时近似系统与原系统平衡点可以任意接近且类型保持一致，这就为我们利用多项式近似系统研究原系统的平衡点及稳定域边界近似提供了理论基础及技术上的可行性。

3 多项式近似系统的能量函数

对于s阶近似系统（2），可构造其能量函数

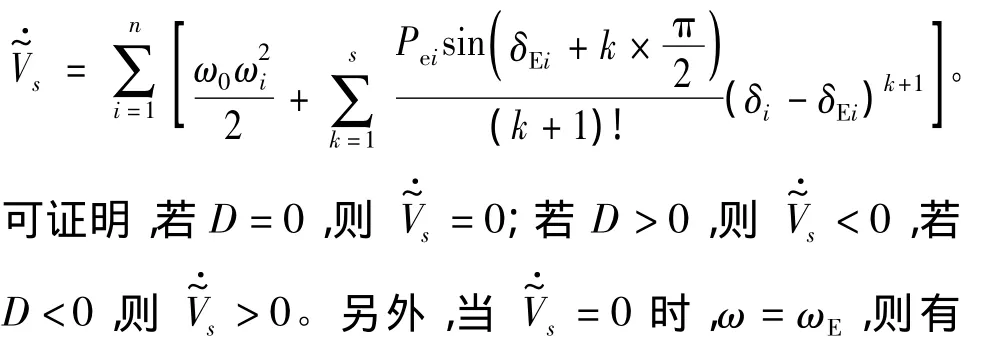
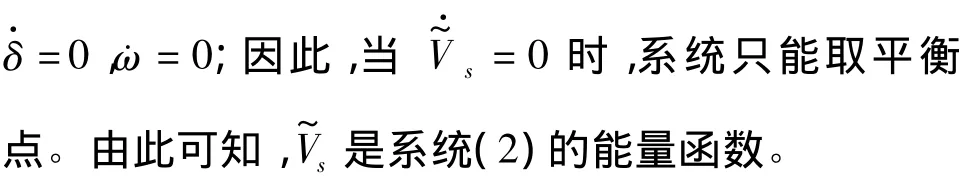
4 算例分析

4.1 单机系统稳定性分析

1）单机系统的多项式近似表示

考虑如下的单机无穷大系统（D=0）·

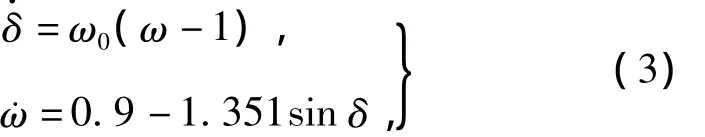
系统存在一个SEP（0.729 1，0），一个不稳定平衡点（UEP）（2.412 5，0）。采用半张量积方法得到其在SEP处的s阶近似系统

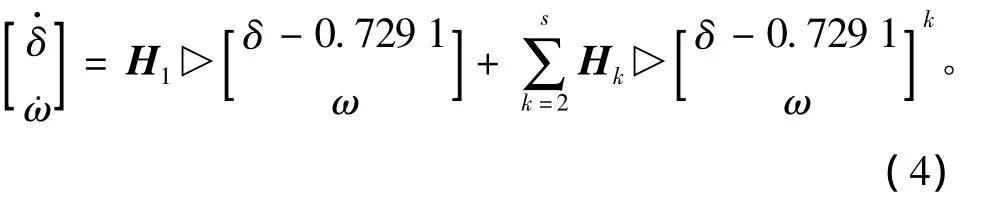
2）单机系统平衡点研究

对单机系统在SEP处分别作2～8阶Taylor展开，得7个近似系统，比较各近似系统平衡点与原系统平衡点之间的关系如下:a）SEP相同，各近似系统均在SEP处Taylor展开得到，因此其SEP与原系统相同;b）UEP随近似阶数的增高与原系统UEP越来越接近，具体地，比较2～8阶近似系统UEP与原系统UEP之间的误差，得到如表1所示结果。从表中可见，随近似阶数的增高，近似系统UEP越来越接近于原系统UEP。同时，以近似系统UEP为初值对原系统UEP求解时原系统均能收敛到其UEP;因此，可利用近似系统UEP近似替代原系统UEP或为初值求取原系统UEP。

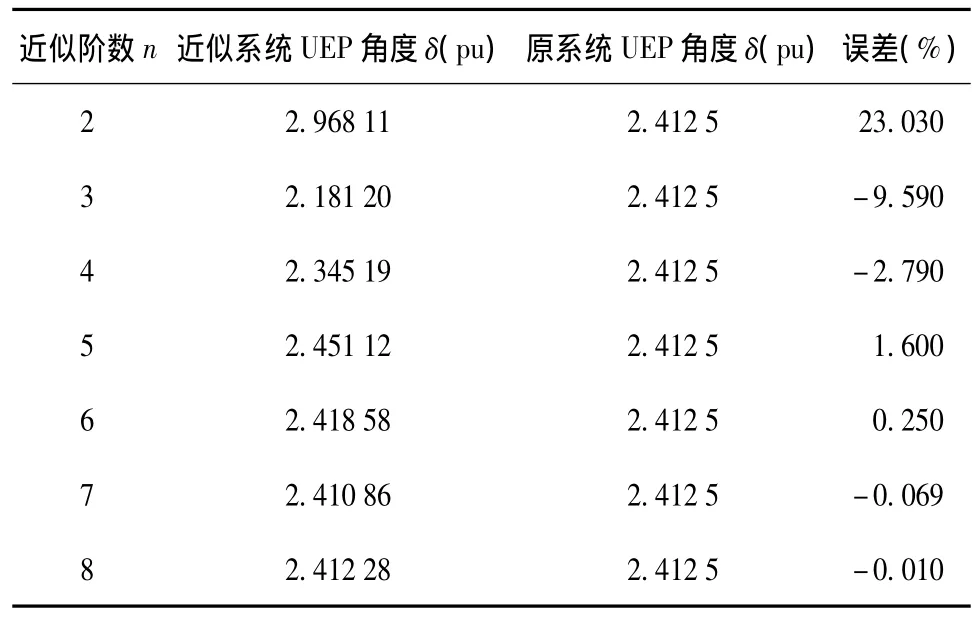
表1 单机无穷大近似系统与原系统UEP比较Table 1 Single-machine infinite-bus（SMIB）system’s UEP and its approximate systems’UEPs

3）单机系统能量函数的构造

对于近似系统（4），构造其能量函数

4）单机系统稳定域边界刻画

稳定域边界近似通常有两类方法:①基于等能量曲面近似稳定域边界［1－2］，采用的是经过 Closest UEP的等能量曲面来近似系统的稳定域边界，该方法具有一定保守性;② 利用稳定域边界上的Controlling UEP的稳定流形的局部近似［18］或者等能量面来近似稳定域边界，可减少保守性。

下面首先利用稳定流形局部近似法求单机无穷大系统及其5～7阶近似系统的稳定域边界局部近似。计算结果如图1所示，其中UEP采用原系统的UEP。实线为原系统准确的稳定域边界及其一次、二次局部近似。虚线分别为5～7阶近似系统的稳定域边界一次、二次局部近似。从图1中可以看出:a）稳定流形局部近似在平衡点附近可较好地近似原系统的稳定域边界;b）随着近似阶数的增高，近似系统稳定域边界局部近似与原系统稳定域边界局部近似越来越接近。

图1 单机无穷大及近似系统稳定域边界局部近似Fig．1 Local approximation of transient stability region boundary for SMIB system and its approximate systems

下面考虑用等能量函数曲面方法近似稳定域边界。具体地，近似系统（4）稳定域边界近似可取为过其UEP的能量函数曲线，即曲线 －c=0，其中c 为过 UEP 的能量值，即 c=|（δuep，ωuep）。

比较2～8阶近似系统稳定域边界与原系统稳定域边界的关系，如图2所示，其中实线为原系统稳定域边界，虚线为各阶近似系统的稳定域边界近似。

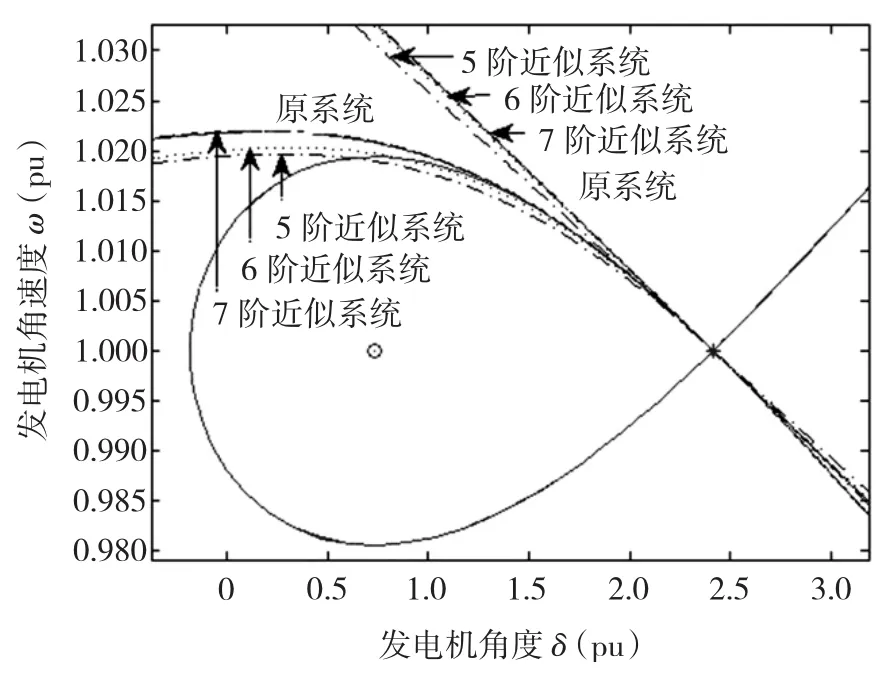
图2 单机无穷大及2～8阶近似系统稳定域边界比较Fig．2 Comparison of transient stability region boundaries between SMIB system and its 2nd-order to 8th-order approximate systems

由图2可见:a）采用能量函数曲线近似系统稳定域边界可在较大范围内近似原系统稳定域边界;b）采用能量函数曲线近似系统稳定域边界时，随着近似阶数的增高，近似系统的稳定域边界近似越来越接近于原系统的稳定域边界。以上两种方法验证了利用多项式近似系统研究原系统稳定域边界近似的合理性。

4.2 多机系统稳定性分析

1）三机系统的多项式近似表示

考察文献［1］中的三机系统模型

2）三机系统平衡点的求取

三机系统（5）共13个平衡点，其中一个SEP，12个UEP，图3给出了三机系统稳定域边界在角度面上的投影，并标注了各平衡点的类型。

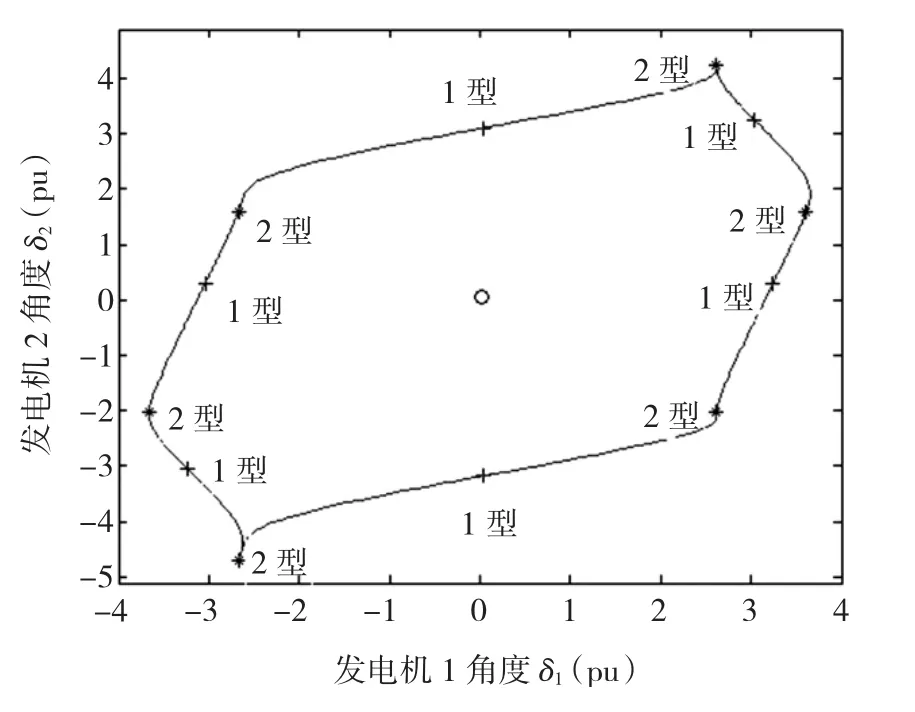
图3 三机系统平衡点及暂态稳定域边界Fig．3 EPs and transient stability region boundary of three-machine system

求取该系统在SEP处的13阶近似系统，并求解其平衡点。图4给出了13阶近似系统与原系统平衡点的关系。其中，圆圈表示原系统平衡点，星形表示近似系统平衡点。从图中标注的平衡点类型可以看出，近似系统与原系统平衡点类型一致。

图4 13阶近似系统与原系统UEP比较图Fig．4 Comparison of UEPs between three-machine system and its 13th-order approximate system

分析图4可知，系统（5）与近似系统（6）的平衡点有如下关系:a）SEP不变;b）近似系统与原系统UEP位置非常接近;c）近似系统双曲UEP性质与原系统一致。这就验证了文献［11］所提到的近似系统与原系统的平衡点的关系，为利用近似系统研究原系统的稳定域边界奠定了基础。

3）三机系统能量函数的构造

对多项式近似系统（6），构造能量函数

4）多机系统稳定域边界刻画

与单机情况相似，本文基于稳定域边界近似的两类方法对13阶近似系统进行了测试，得到如图5和图6所示的结果。

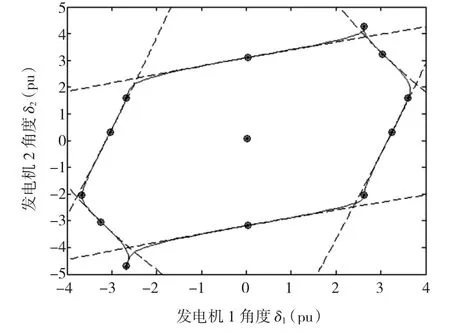
图5 三机系统13阶近似系统稳定域边界二次近似Fig．5 Quadratic approximation of transient stability region boundary of three-machine system’s 13th-order approximate system

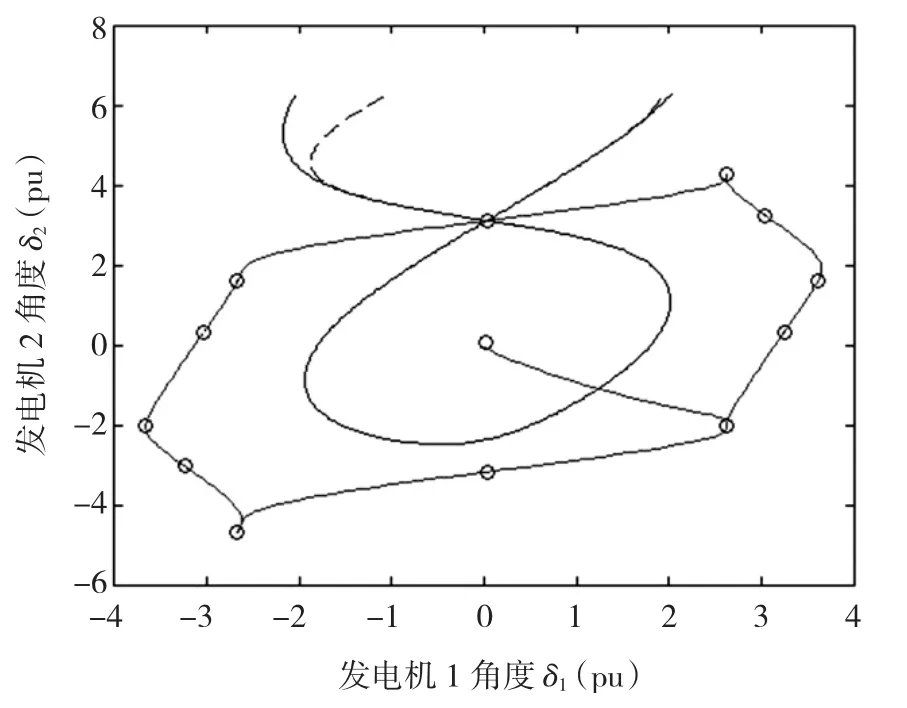
图6 三机系统及其13阶近似系统势能界面Fig．6 Closest UEP’s potential energy boundary surface of three-machine system and its 13th-order approximate system

首先采用局部近似方法，利用稳定域边界上所有1型UEP的稳定流形局部近似来构成整个稳定域边界，结果如图5所示，其中实线表示原系统稳定域边界在角度面上的投影，虚线表示13阶近似系统稳定域边界的二阶近似在角度面上的投影。从图5可以看出，利用13阶近似系统稳定域边界的二阶近似可以很好地近似原系统的稳定域边界。

其次采用通过Closet UEP的等能量曲面来近似稳定域边界，其结果如图6所示，其中，实线为原系统过Closest UEP的等能量曲面在角度面上的投影，虚线为13阶近似系统过Closest UEP的等能量曲面在角度面上的投影。由图6可见，近似系统等能量曲面与原系统的等能量曲面非常接近。

由上述测试结果可以看出，利用高阶近似系统的稳定域边界近似可较好地近似原系统的稳定域边界，因此可以考虑利用近似系统研究原系统的稳定域边界。由于本文对原非线性系统的近似系统的求取及稳定域边界的近似刻画均采用了半张量积方法，可方便地利用计算机自动实现不稳定平衡点的计算和能量函数的构造，有望实现电力系统暂态稳定分析全过程的“自动化”。

5 结论

利用半张量积方法求得一般电力系统非线性模型的多项式近似系统，并通过分析表明利用多项式近似系统分析原系统的平衡点及稳定域边界近似是可行的，从而可在电力系统暂态稳定分析中充分利用多项式系统在分析与计算上的优势。对单机无穷大系统及三机系统的仿真试验验证了本文所提方法的有效性。从某种意义上讲，将一般非线性系统表述为多项式系统，也是一种有效的“约化”。但必须说明的是，虽然多项式系统是一类“最简洁”的非线性系统，但其分析与计算仍然是困难的。本文的工作只是一个初步尝试，下一阶段的重点是充分利用代数几何等先进数学工具，最大程度地提高半张量积方法的工程实用性。

［1］CHIANG H D，CHU C C，CAULEY G．Direct stability analysis of electric power systems using energy functions:theory，applications and perspective［J］．Proceedings of the IEEE，1995，83（11）:1497－1529．

［2］CHIANG H D，WU F F，VARAIYA P P．A BCU method for direct analysis of power system transient stability［J］．IEEE Transactions on Power Systems，1994，9（3）:1194 －1208．

［3］SCRUGGS J T，MILI L．Dynamic gradient method for PEBS detection in power system transient stability assessment［J］．Int．Journal of Electrical Power＆Energy Systems，2001，23（2）:155－165．

［4］TREINEN R T，VIITTAL V，KLIEMANN W．An improved tech-nique to determine the controlling unstable equilibrium point in a power system ［J］．IEEE Transactions on Circuits and Systems（Ⅰ）:Fundamental Theory and Applications，1996，43（4）:313－323．

［5］NAZARENO I S，ALBERTO L F C，BRETAS N G．Problems in the precise detemination of BCU’s controlling unstable equilibrium points and PEBS’s exit point method in real-time transient stability analysis［C］∥2004IEEE/PES Transmission＆Distribution Conference＆Exposition．Latin America:IEEE/PES，2004:475－480．

［6］NAZARENO I S，ALBERTO L F C，BRETAS N G．Robust computation of the controlling unstable equilibrium points in transient stability analysis［C］∥Power Tech，St．Petersburg．Russia:Power Tech，IEEE，2005:1－7．

［7］LEE J，CHAING H D．Computation of multiple type-one equilibrium points on the stability boundary using generalized fixed-point homotopy methods［C］∥Proceedings of the2001IEEE International Symposium on Circuits and Systems．Sydney:ISCAS，2001，3:6－9．

［8］LEE J，CHIANG H D．Convergent regions of the Newton homotopy method for nonlinear systems:theory and computational applications［J］．IEEE Transactions on Circuits and Systems（Ⅰ）:Fundamental Theory and Applications，2001，48（1）:51 －66．

［9］LEE J，CHIANG H D．A singular fixed-point homotopy method to locate the closest unstable equilibrium point for transient stability region estimate［J］．IEEE Transactions on Circuits and Systems（Ⅱ）:Express Briefs，2004，51（4）:185 －189．

［10］侯凯元，闵勇．基于伴随系统理论的电力系统主导不稳定平衡点求解方法［J］．现代电力，2005，22（1）:21－26．

HOU Kaiyuan，MIN Yong．Computing the controlling unstable equilibrium point based on the theory of adjoint systems［J］．Modern Electric Power，2005，22（1）:22 －26．

［11］孙玉娇，刘锋，梅生伟．非线性系统的多项式近似表示及电力系统应用（Ⅰ）——理论篇［J］．电机与控制学报，2010，14（8）:19－23，30．

SUN Yujiao，LIU Feng，MEI shenwei．Polynomial approximation of a nonlinear system and its application to power system（Ⅰ）:theoretical justification［J］．Electric Machines and Control，2010，14（8）:19－23，30．

［12］程代展．矩阵的半张量积理论与应用［M］．北京:科学出版社，2007:1－134．

［13］COX D A，LITTLE J，O’SHEA D．Using Algebraic Geometry［M］．Berlin:Springer，2005:1－115．

［14］BENALLOU A，MELLICHAMP D，SEBORG D．On the number of solutions of multivariable polynomial systems［J］．IEEE Transactions on Automatic Control，1983，28（2）:224 －227．

［15］MORGAN A．Solving Polynomial Systems Using Continuation for Engineering and Scientific Problems［M］．Englewood Cliffs，N J:Prentice-Hall，1987:1 －143．

［16］刘安心．求多项式方程组全部解的连续法［J］．工程兵工程学院报，1999，14（1）:80－85．

LIU Anxin．Continuation method of solving all solutions of polynomial equations［J］．Journal of Engineer Corps and Egineering Institute，1999，14（1）:80 －85．

［17］LI Tien-Yien，TSAI Chih-Hsiung．HOM4PS-2.0 para:parallelization of HOM4PS-2.0 for solving polynomial systems［J］．Parallel Computing，2009，35（4）:226－238．

［18］ 马进．基于能量的电力系统暂态稳定分析与控制［D］．北京:清华大学，2003．

（编辑:张静）