包含零矢量的永磁同步电机直接转矩控制

卢达， 赵光宙， 李楠

（浙江大学电气工程学院，浙江杭州 310027）

0 引言

直接转矩控制（DTC）技术采用定子磁场定向，依据给定电磁转矩与实际电磁转矩、给定定子磁链与实际定子磁链的偏差，通过选择合适的电压空间矢量控制电机的电磁转矩和定子磁链。与气隙磁场定向、意在解耦的矢量控制相比，由于DTC采用的滞环控制本身不受电机参数变化影响，系统鲁棒性得到提高［1］，同时省去了坐标变换，转矩响应明显加快。但是由于滞环控制只能提供电压矢量的选择原则却无法计算出准确的电压矢量［1］，而逆变器开关频率又不够高［2］，并且在电机运行中定子电阻阻值会变化等原因［3］，系统输出的电磁转矩脉动较大，限制了DTC的应用范围。如何抑制DTC转矩脉动，一直是DTC研究者们关注的焦点。

永磁同步电机（PMSM）具有体积小、效率高、转动纹波系数小等优点，鉴于DTC在异步电机中的成功应用和PMSM研制的突破性进展，近年来DTC在PMSM中的应用已逐渐成为运动控制的研究热点。

传统研究认为，在PMSM DTC中零矢量不能起到类似于在感应电机DTC中减少电磁转矩的作用，故并不提倡使用它［4］。文献［5］根据同步电机和异步电机产生转矩增量机理的不同，分析了PMSM系统中的零矢量，认为它具有保持电磁转矩的功能，提出在PMSM DTC中引入零矢量可以让电磁转矩在滞环范围内基本恒定，可有效减少转矩脉动，并且不牺牲DTC的快速响应特性。

PMSM模糊DTC中加入零矢量的优势在于，在不增加硬件成本和软件复杂性的前提下，可以明显地提高系统的动静态性能。现有文献中的PMSM模糊DTC技术大多没有利用零矢量［11－13］。近年来，有些学者尝试将零矢量加入模糊规则表［2，14］，但这些方法并没有充分发挥零矢量的特性。本文提出的改进的基于包含零矢量模糊逻辑的PMSM DTC技术，改进了模糊控制器，经仿真验证合理有效地利用了零矢量的特性，性能优于以往的PMSM模糊DTC技术。

1 改进的包含零矢量PMSM模糊DTC

为简化分析，本文主要讨论永磁同步隐极电机。在PMSM系统中，通常逆变器能产生8种电压空间矢量，相邻电压矢量的角平分线把空间矢量平面分为6个扇区，如图1所示。6个非零矢量互差π/3，沿空间矢量平面半径方向平分各扇区角。2个零矢量位于空间矢量平面的中心。

PMSM定子磁链在静止坐标系中可以表示为

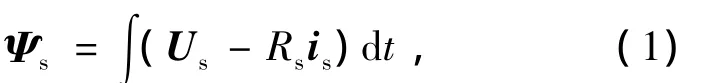
式中:Ψs为定子磁链;Us为定子电压空间矢量;Rs为定子电阻;is为定子电流。

当忽略定子电阻的影响时，PMSM定子磁链的变化量可表示为

式中:T为采样周期;ΔΨs为定子磁链经过一个采样周期的变化量。

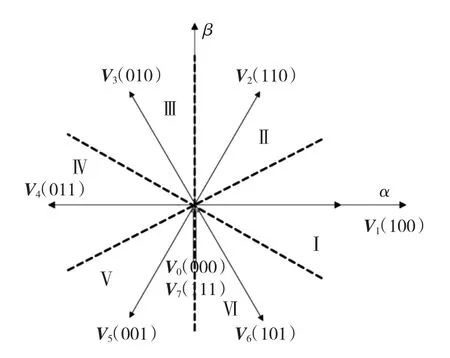
图1 电压空间矢量Fig．1 Voltage space vectors

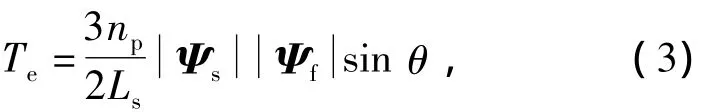
式中:np为极对数;Ls为定子电感;Ψf为转子磁链;θ为定转子磁链的夹角。

如果有一刹那，上帝忘记我是一只布偶并赋予我片刻生命，我可能不会说出我心中的一切所想，但我必定会思考我所说的一切。

定转子磁链夹角变化（Δθ）由2部分组成，即定子磁链角变化（Δθs）和转子磁链角变化（Δθr）。当零矢量作用时，由式（2）可知定子磁链不变，即Δθs为零，Δθ等于Δθr。Δθr只受转速控制，由于机电时间常数很大，在一个采样周期内，Δθr几乎不变。由式（3）可知，定转子磁链幅值不变时，控制它们之间的夹角便可控制电磁转矩的变化［4］。零矢量作用时Δθ几乎不变，故可近似的认为零矢量具有保持电磁转矩的作用。实验也证明［5－15］，零矢量作用时由Δθr造成的转矩落差与额定转矩相比不会太大。

1.1 控制系统结构

与传统的DTC不同，改进的包含零矢量PMSM模糊DTC系统中用模糊控制器（FLC）代替了转矩、磁链滞环比较器和开关表。FLC是系统中的核心部分，其输出用于驱动PWM逆变器，使PMSM按要求运行。图2为包含零矢量的PMSM模糊DTC系统框图，其中为参考速度，ωr为反馈速度;为参考定子磁链幅值，Ψs为估计定子磁链幅值，ΔΨs表示参考定子磁链和估计定子磁链之差。参考转矩是速度PI调节器的输出，T为估计转矩，ΔT表ee示参考转矩和估计转矩之差。为映射前定子磁链角，θs为映射后定子磁链角。VS为电压空间矢量。

由式（2）可知，定子电压空间矢量可控制定子磁链的变化。PMSM的电磁转矩方程为Ia、Ib、Ic为传感器检测的电流信号。

图2 包含零矢量PMSM模糊DTC的系统框图Fig．2 Diagram of PMSM DTC based on fuzzy logic with zero-voltage vector

1.2 改进的包含零矢量FLC设计

改进的包含零矢量PMSM模糊DTC系统中的FLC由模糊化、模糊推理、解模糊和模糊规则库4部分组成（见图3）。FLC的输入量为定子磁链角、电磁转矩误差和定子磁链误差，FLC的输出量为逆变器控制信号。

图3 模糊控制器结构图Fig．3 Diagram of fuzzy logic controller

定子磁链角在扇区Ⅰ［0，gπ/3］中根据角度大小划分为［0，gπ/6］（NS）、［π/6，gπ/3］（PS），隶属函数如图4（a）所示。使用式（4）可将空间矢量平面内任意角度映射到这个范围［16］，这样会有效减少模糊规则的数量，提高运算速度。

式中:θ*为映射前定子磁链角;θ为映射后LFC输入量;round（）为取整符号。

电磁转矩误差分为5个模糊子集，负大偏差（NB）、负小偏差（NS）、零偏差（ZO）、正小偏差（PS）、正大偏差（PB），隶属函数如图4（b）所示。定子磁链误差分为3个模糊子集，分别是负偏差（NS）、零偏差 （ZO）、正偏差 （PS），隶属函数如图4（c）所示。FLC输出为扇区Ⅰ的逆变器控制信号，分为 7 个模糊子集（V0、V1、V2、V3、V4、V5、V6），隶属函数如图4（d）所示。

图4 FLC隶属函数对比图Fig．4 Comparison of membership functions

根据式（2）、式（3）、输入输出量的各隶属函数以及DTC调试经验，可以制定出模糊规则库，模糊规则用IF-THEN语句表示，即

由于逆变器只能产生8种电压空间矢量，所以在大多数情况下逆变器输出不能同时满足矫正电磁转矩误差和矫正磁链误差的需要。根据经验，磁链误差更容易矫正，故当矫正电磁转矩误差和磁链误差发生矛盾时，应优先考虑电磁转矩误差的矫正。表1为本文仿真中用到的模糊规则库，共包含30条规则。

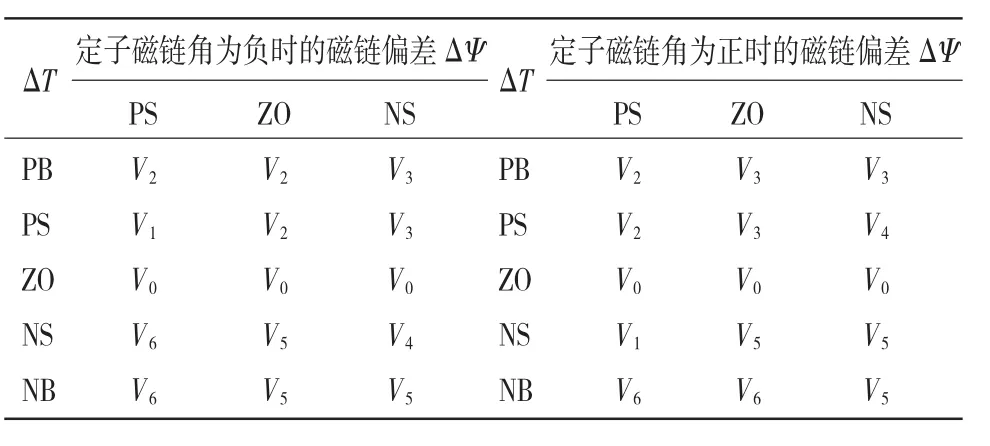
表1 模糊规则库Table 1 Fuzzy control rules

采用重心法解模糊，可得到精确的扇区Ⅰ逆变器控制信号输出。把这个值反映射回空间矢量平面，可以得到控制整个空间矢量平面的逆变器控制信号。

1.3 改进的包含零矢量的FLC分析

确定FLC中各输入输出量的隶属度函数对控制效果有重要影响。在以往的包含零矢量的FLC实现方法［2，14］中，定子磁链角的隶属函数如图4（e）所示，电磁转矩误差的隶属函数如图4（f）所示，定子磁链误差的隶属函数如图4（g）所示，电压空间矢量的隶属函数如图4（h）所示。

电磁转矩误差的ZO子集表示转矩误差较小，可以使用零矢量，其它子集表示转矩误差较大，应该使用相应的非零矢量。如果将ZO的隶属函数与其它子集的隶属函数相模糊，由模糊规则库及解模糊方法可知，系统中能够使用零矢量的概率将非常小，无法充分发挥零矢量的特点。在电压空间矢量的子集中，V0表示使用零矢量。零矢量与其它电压空间矢量的最显著区别在于空间位置不同，它位于空间矢量平面的中心而不是半径。FLC中利用重心法解模糊，是各模糊输出加权平均以得到精确的结果。如果V0的隶属函数面积不为0，零矢量就会误参与半径方向上非零矢量之间的加权平均，使解模糊量偏小，导致失控。确定定子磁链误差的隶属函数可以不考虑零矢量，因为根据模糊规则库，零矢量的使用与否只和转矩误差的大小有关。

以往的包含零矢量的FLC实现过程中通常将转矩ZO子集的隶属函数选取的很窄，这样虽能够一定程度上避免零矢量干扰非零矢量，但是却限制了零矢量的使用，失去了包含零矢量的本意，提高了逆变器所需的开关频率，大大增加了系统损耗。为充分体现零矢量的作用效果，在图4（f）中扩大了ZO子集隶属函数的跨度，将其与图4（b）中ZO子集隶属函数的跨度相等。

表2对比了在不同情况下两种FLC的输出，其中 θs=0．3，ΔΨs= －0．003。表中的量为 FLC 输出的电压空间矢量，由解模糊后的精确值取整得到，括号内为解模糊后的精确值。

表2 不同控制技术中FLC的输出比较Table 2 Comparison of outputs of FLC in different strategies

第一种情况，定子磁链应减小，转矩偏差应保持不变。改进的FLC输出零矢量，满足控制要求。以往的FLC输出的电压空间矢量偏小，会导致定子磁链减小、转矩增大，控制失败。

第二种情况，定子磁链应减小，转矩偏差应保持不变。改进的FLC输出零矢量，满足控制要求。以往的FLC输出的电压空间矢量偏小，会导致定子磁链和转矩均增大，控制失败。

第三种情况，定子磁链应减小，转矩应增大。这时转矩ZO子集隶属度为0，FLC中不使用零矢量，两种的FLC输出均满足控制要求。

2 仿真结果

为验证改进的包含零矢量PMSM模糊DTC技术的有效性，本文在 Matlab/Simulink下进行了仿真研究，并与以往的包含零矢量PMSM模糊DTC控制技术进行了对比（见图4）。本文仿真实验采用的电机参数:直流母线电压300 V，额定电流2.3 A，额定转速3 750 r/min，极对数2，转子磁链0.184 8 Wb，定子电阻0.184 8 Ω，d轴电感0.014 H，q轴电感0.014 H。系统采样周期为 50 μs，给定转速为1000 r/min，给定定子磁通为0.2 Wb。负载电磁转矩值初始时为零，在0.06 s时阶跃到1（N·m），然后保持不变。

图5为本文提出的控制技术的转速响应，图6为两种控制技术的转矩响应，图7为两种控制技术的定子磁链响应。由图6可知，改进算法的转矩脉动明显小于相同条件下以往算法的转矩脉动，而负载转矩变化时电磁转矩的响应速度依旧迅速。由图7可知，当让零矢量充分作用时，以往算法的磁链波动很大、有很多尖峰，而改进算法的磁链波动显著减小，也不存在明显的尖峰。仿真结果表明，以往的包含零矢量PMSM模糊DTC中，零矢量的作用体现的并不明显，当转矩ZO子集的隶属函数较宽时，还会干扰非零矢量的作用过程。本文提出的技术能使系统运行稳定，获得优异的动静态性能，具有比以往的包含零矢量PMSM模糊DTC控制技术更好的转矩和磁链响应。

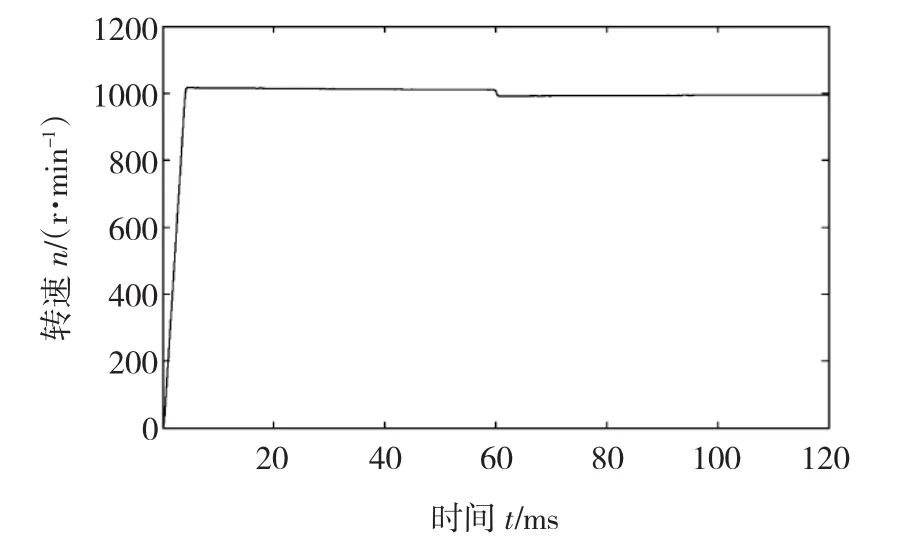
图5 改进技术的速度响应Fig．5 Speed responses in proposed strategy

图6 两种控制技术的转矩响应Fig．6 Torque responses in different control strategies for PMSM

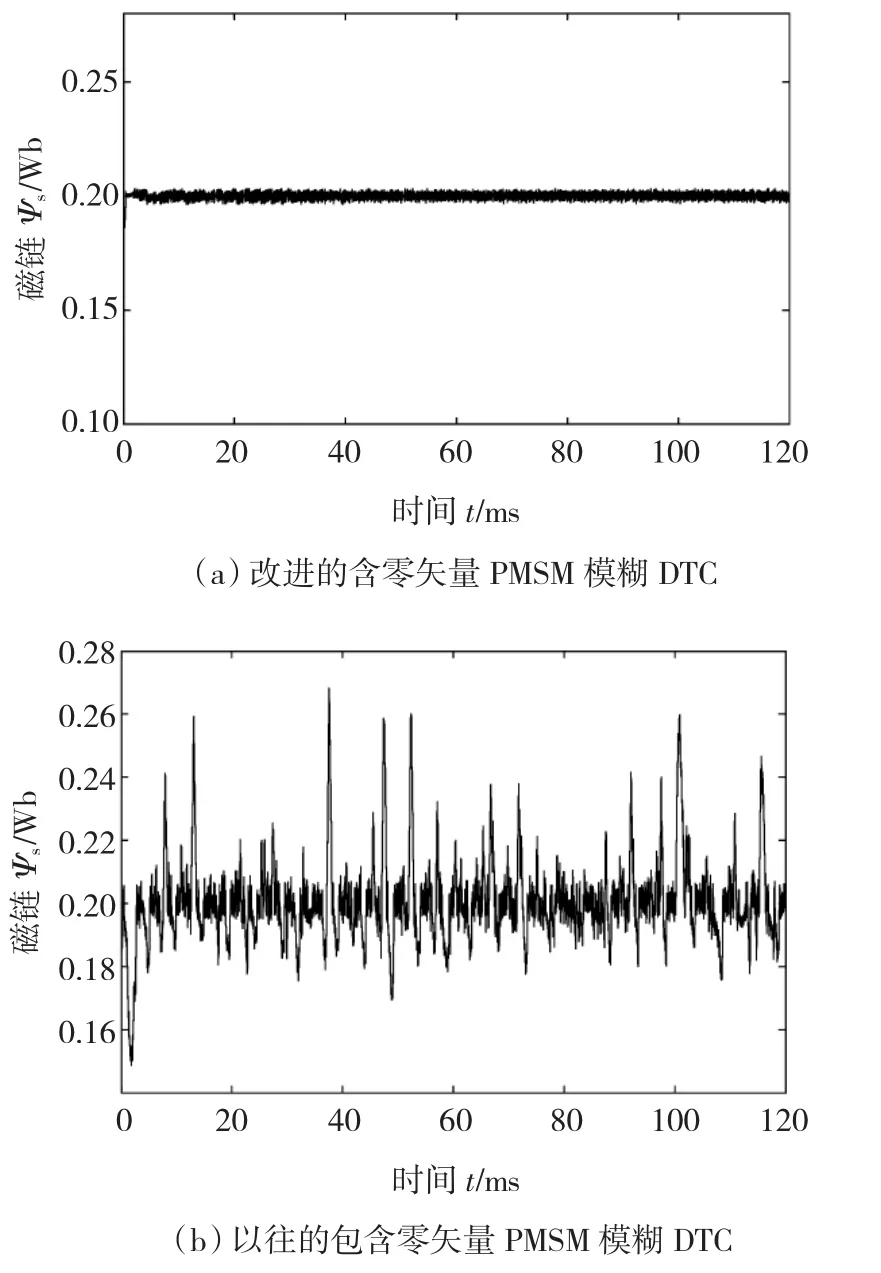
图7 两种控制技术的定子磁链响应Fig．7 Stator flux responses in different control strategies for PMSM

3 结论

改进包含零矢量的PMSM模糊DTC技术，使零矢量保持电磁转矩的特性得到充分发挥。经过仿真验证，取得了比原有包含零矢量的PMSM模糊DTC技术更优越的动静态性能。但同时可以看出，本文提出的改进方法没有能完全消除转矩脉动，算法还有进一步改进的空间。今后可以尝试将这种包含零矢量的PMSM模糊DTC技术与其他控制算法结合，以进一步提高系统控制性能。

［1］ 王成元，夏加宽，孙宜标，等．现代电机控制技术［M］．北京:机械工业出版社，2009:173．

［2］SHENG Yifa，YU Shouyi，HONG Zhennan，et al．Switching frequency optimize and fuzzy logic based direct torque control of permanent magnetic synchronous motor［C］∥Proceedings of the26th Chinese Control Conference．Beijing:Beijing University of Aeronautics＆ Astronautics Press，2007:374－379．

［3］HAQUE M E，RAHMAN M F．A PI stator resistance compensator for a direct torque controlled interior permanent magnet synchronous motor drive［C］∥5th International Power Electronics and Motion Control Conference．Beijing:International Academic Publishers，2000:175 －179．

［4］ZHONG L，RAHMAN M F，HU Wenyu，et al．Analysis of direct torque control in permanent synchronous motor drives［J］．IEEE Trans on Power Electronics，1997，12（3）:528－536．

［5］田淳，胡育文．永磁同步电机直接转矩控制系统理论及控制方案的研究［J］．电工技术学报，2002，17（1）:7－11．

TIAN Chun，HU Yuwen．Study of the scheme and theory of the direct torque control in permanent magnet synchronous motor drives［J］．Transactions of China Electrotechnical Society，2002，17（1）:7－11．

［6］许力．智能控制与智能系统［M］．北京:机械工业出版社，2006:104．

［7］XU Yanping，ZHONG Yanru，LI Jie．Fuzzy stator resistance estimator for a direct torque controlled interior permanent magnet synchronous motor［C］∥Proceedings of8th Annual ICEMS Electrical Machines and Systems．Beijing:International Academic Publishers，2005:438 －441．

［8］黄释贤．适应模糊滑模速度控制器与永磁同步马达之研究［D］．台湾:成功大学，2007．

［9］KOUTSOGIANNIS Z，ADAMIDIS G，FYNTANAKIS A．Direct torque control using space vector modulation and dynamic performance of the drive，via a fuzzy logic controller for speed regulation［C］∥The12th European Conference on Power Electronics and Applications．Aalborg，Denmark:IEEE，2007:1 －10．

［10］刘军，刘丁，吴浦升，等．基于模糊控制调节电压矢量作用时间策略的永磁同步电机直接转矩控制仿真研究［J］．中国电机工程学报，2004，24（10）:148－152．

LIU Jun，LIU Ding，WU Pusheng，et al．The simulation analysis of permanent magnet synchronous motor based on the strategy of modulating the time of voltage vector［J］．Proceeding of the CSEE，2004，24（10）:148－152．

［11］孙丹，贺益康，智大为．基于模糊逻辑的永磁同步电动机直接转矩控制［J］．电工技术学报，2003，18（1）:33－38．

SUN Dan，HE Yikang，ZhI Dawei．Direct torque control of a permanent magnet synchronous motor based on fuzzy logic ［J］．Transactions of China Electrotechnical Society，2003，18（1）:33－38．

［12］SOLIMAN H，ELBULUK M E．Improving the torque ripple in DTC of PMSM using fuzzy logic［C］∥Industry Applications Society Annual Meeting．Edmond，Canada:IEEE，2008:1 －8．

［13］AKBAR Rahideh．High performance direct torque control of a PMSM using fuzzy logic and genetic algorithm［C］∥Proceedings of Electric Machines＆Drives Conference．Antalya:Academic Press，2007，2:932 －937．

［14］李勇，罗隆福．基于模糊控制的永磁同步电动机直接转矩控制［J］．微电机，2006，39（3）:37－40．

LI Yong，Luo Longfu．The direct torque control system of PMSM based on fuzzy control［J］．Micromotors，2006，39（3）:37－40．

［15］贾洪平，贺益康．永磁同步电机直接转矩控制中零矢量作用的研究［J］．电气传动，2006，36（4）:13－16．

JIA Hongping，HE Yikang．Study on null vector in a direct torque controlled permanent magnet synchronous motor［J］．Electric Drive，2006，36（4）:13 －16．

（编辑:张静）