移动机器人模糊Q－学习沿墙导航

徐明亮， 柴志雷， 须文波

（1．无锡城市职业技术学校 电子信息系，江苏无锡 214063;2．江南大学 信息工程学院，江苏无锡 214122）

0 引言

导航是移动机器人的一项重要的功能，是移动机器人完成其他智能行为的基础。沿墙导航控制是指机器人在和墙保持一定距离的情况下沿墙运动，从更一般意义上来说实际上是机器人与物体保持一定距离并沿物体轮廓运动［1］。因此沿墙导航实际上既可以使机器人实现障碍物的避碰［2］，也可以实现在未知环境的导航［3］。

移动机器人的反应式导航是一种直接在机器人的感知和行为之间建立映射关系的导航方法。它具有灵活和执行快速的特点而成为移动机器人在未知和快速变化环境中导航的重要方法。已有许多学者提出了不同的反应式导航方法，比如文献［4］采用引力势场法进行导航。文献［5］采用基于模糊规则的反应式导航控制器。这些方法通常基于具体的环境模型，需要较多的先验知识，同时对变化的环境不具有自适应能力。

强化学习能够在没有先验知识的情况下通过与环境的交互获得由状态到动作的策略，因此基于强化学习的机器人导航受到众多研究者的广泛关注。文献［6］中采用Q-学习来对模糊规则进行调整，但模糊规则则是根据机器人的系统特性手工建立。文献［7］也采用类似技术，其特点是用RBF网络逼近选定的若干个离散动作的Q-值，网络权值利用Q-学习来调整。而RBF网络隐层节点的中心和宽度却要由样本来确定。文献［8］采用CMAC神经网络实现了Q-值函数的逼近，该方法涉及到输入参数的离散化，离散化的粒度也将影响系统的性能。文献［9］利用FNN来逼近Q－值函数和策略函数，而这些函数都是建立在若干个选定的离散动作的基础之上，使得系统过于复杂。文献［10］是用模糊推理系统来逼近Q-值函数，每一条规则对应一个由若干个选定的离散动作所构成的向量，每一个规则的输出动作由规则内部的离散动作通过竞争的方法产生，控制器的输出动作由各个规则的输出动作根据当前状态在各个规则所导出的状态值进行加权。在这些方法中，导航控制器输出取决于预先选定的离散动作。这些离散动作的选择影响导航控制器的性能，而如何选择这些种子动作也没有任何先验知识可用。另外这些方法中的Q-学习从本质上来说是基于 actor-critic 方法的［11］。

为避免种子动作的选择，我们用模糊神经网络直接对强化学习中的Q-值函数进行逼近，即网络的输入为状态动作对，而非相关文献中的状态，利用函数优化技术产生控制器输出动作。同时在学习过程中引入网络节点自适应构建和参数自适应调整方法，减少人工干预。

1 基于模糊神经网络的Q-学习

Q-学习的主要目标是通过与环境的交互获得表征策略的状态动作对的Q-值函数。Q-学习中状态动作对的Q值按照下式进行更新:

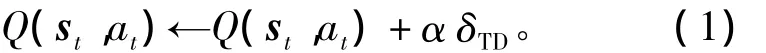
其中:st为当前状态;at为当前状态下选择执行的动

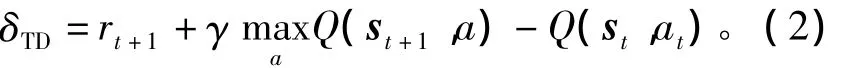
其中:γ为折扣因子，rt+1为学习agent在状态st执行动作at后转移到状态st+1时所获得的立即奖赏。经典的Q-学习是以查找表来描述离散空间状态动作对的值函数。对于连续空间下的Q学习，直接的方法是将连续空间进行离散化处理。而对于离散的粒度选择，往往没有任何先验知识可用。离散粒度过大将会导致系统性能下降，甚至学习不成功;过小也会使学习速度下降。为克服离散化所产生的弊端，研究者普遍采用具有泛化功能的神经网络或模糊推理系统来逼近Q值函数。

模糊神经网络是模糊推理系统和神经网络相结合的产物，它既拥有模糊推理系统便于知识的表达和便于在系统中嵌入已有知识的优点，也拥有神经网络的自学习自组织的特点，因此在函数逼近中得到广泛应用。因此我们采用模糊神经网络来逼近Q值函数。

1.1 网络结构

用于对Q值函数进行直接逼近的模糊神经网络结构如图1所示。第一层为输入层，它将由状态s和动作a构成的向量x=（s1，…，sm，a）T直接传送到下一层。状态空间s为m维，记向量x维数为n，则n=m+1。第二层为模糊化层，其中每个节点代表一个语言变量。该层的作用是计算各个分量在不同语言变量中的隶属度。各个语言变量的隶属度函数采用高斯函数。输入向量第i个分量的第j个语言变量的隶属度函数为作;α 为学习率;δTD为时间差分（temporal difference，TD）。一步时间差分δTD计算式为其中:μij和σij分别为该隶属度函数的中心和宽度;J为该分量的语言变量的个数。

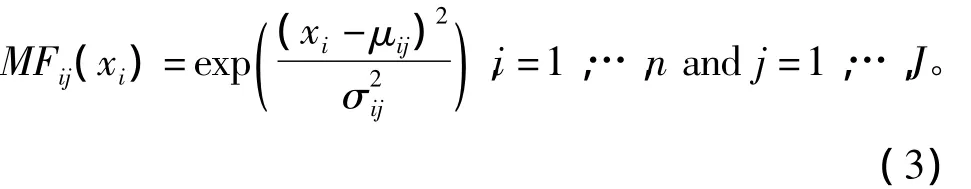
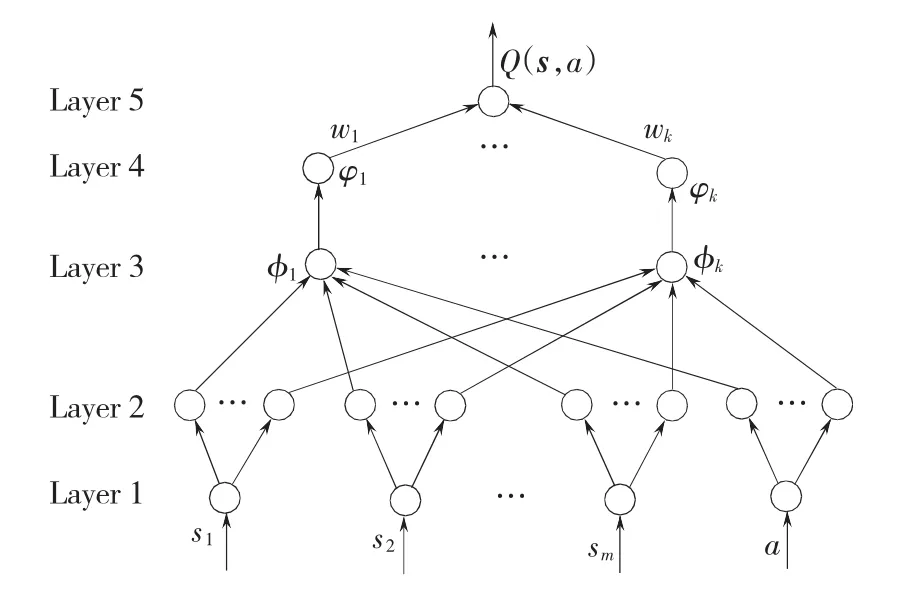
图1 网络结构Fig．1 The architecture of network

第三层为T-norm运算层，该层计算每个规则的发射强度。第k条规则的发射强度为

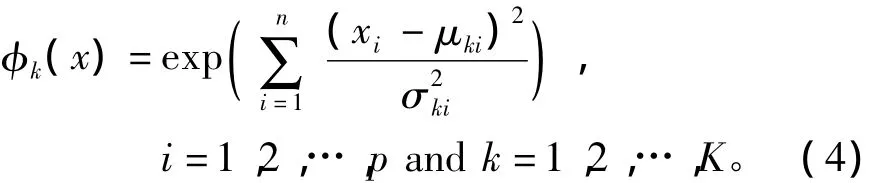
第四层为归一化层，对每一条规则的发射强度进行归一化处理。第k条规则的归一化后的发射强度为

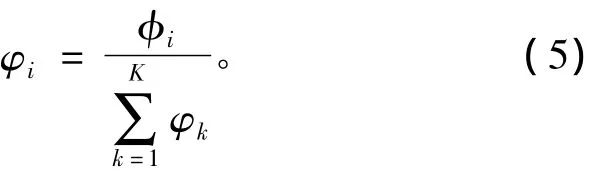
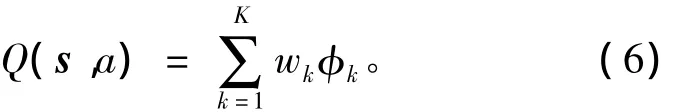
wk是第k条规则的后件。

1.2 结构与参数学习

模糊规则可以根据样本的ε完整性［12］来建立，但ε完整性不能充分体现每个分量对系统性能有不同影响。在文献［13］中，RBF网络隐层节点根据当前样本与隐层节点中心最小距离和误差进行自适应添加。在这些方法中没有考虑系统性能对输入向量中的不同分量有不同的敏感程度。如果对这些分量不加区别，为保证系统性能，就要照顾到对系统性能敏感的分量，因此必须采用较细的分辨率，这样将导致规则数或隐层节点数目过多。对系统性能敏感的分量应采用较细的分辨率，而对系统性能不敏感的分量应采用较粗的分辨率。这样可以减少节点数目，减小系统计算量，加快学习速度。因此考虑不同分量具有不同分辨率的模糊规则构造的条件为

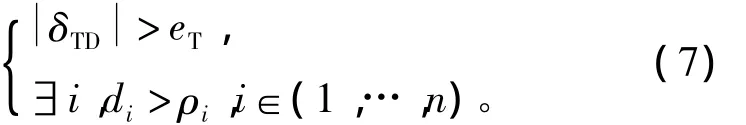
第五层为解模糊层即输出层，采用重心法进行解模糊，输出为输入状态动作对的Q值，即

式中:ρi为第i个分量的分辨率;eT为TD误差阈值;di为输入状态动作对的第i个分量和该分量全部语言变量的隶属度函数中心的最小距离，即

其中:xti为在时间t的状态动作对的第i个分量。

如果当前状态动作对满足式（7）的条件，系统就构造一个新的模糊规则。为描述方便，记

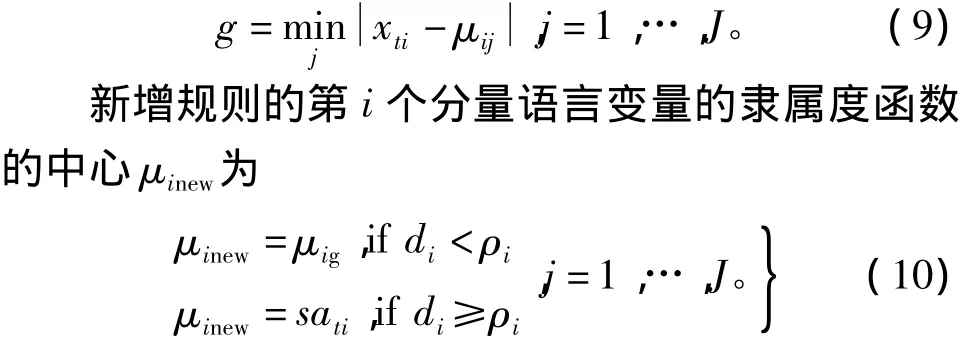
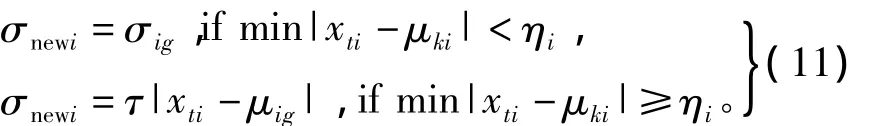
式中参数τ为重叠系数。ηi为第i个分量的分辨率。新规则的后件wnew为

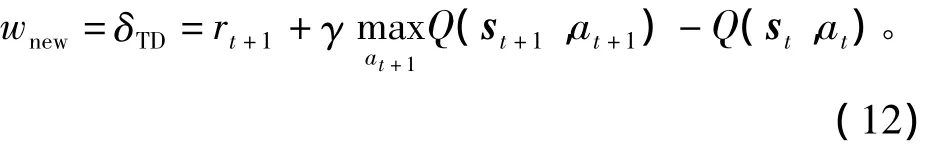
该规则第i个分量的隶属度函数的宽度为

在学习的初始阶段，系统没有任何规则，可以以第一个状态动作对作为隶属度函数中心建立第一个规则，规则的宽度设为［τρ1，…，τρn］。对于后续的状态动作对则根据式（7）来判断是否创建新的规则。

当无需增加新规则时，即状态动作对不满足规则构建的条件时，可以采用梯度下降法对规则的前件和后件中的相关参数进行调整。但由于梯度下降法容易陷入局部最优，因此采用卡尔曼滤波法对相关参数进行调整［14］。

令规则中全部可调参数构成的向量为v=［w1，μT1，σT1，…，wK，μTK，σTK］T，根据卡尔曼滤波方法其更新式为

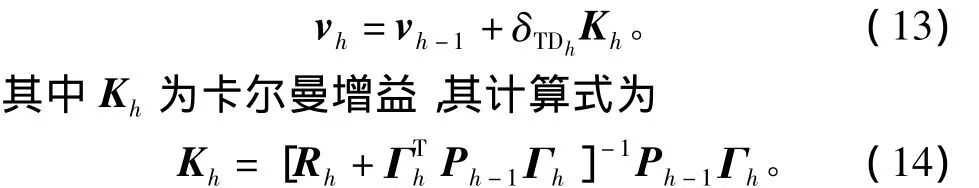
其中Γh为各个参数的梯度向量，由式（3），（4），（5），（6）可以推导出

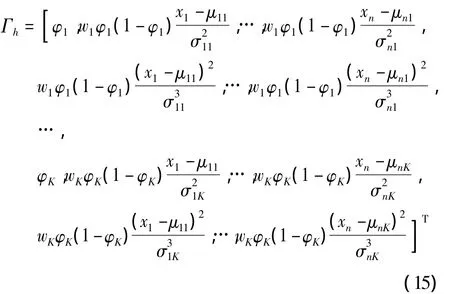
其中Rh为测量噪声方差，Ph为协方差矩阵，其更新式为

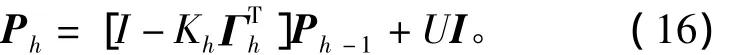
其中U是一个标量，表示在梯度方向上的随机步长，I为单位矩阵。如果参数v的长度为N，Ph是一个N×N正定对称矩阵，当新增一个规则时，可调参数也将增加，矩阵Ph的维数按下式增加，即

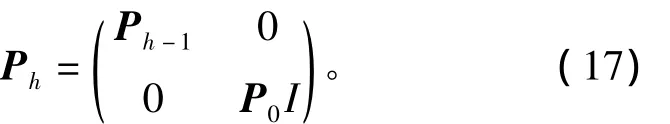
其中P0为新增规则的初始化参数。

1.3 动作输出与搜索和利用平衡

为获得最大的累积报酬，学习主体在任何状态下总是选择具有最大Q值的动作，即贪婪动作:

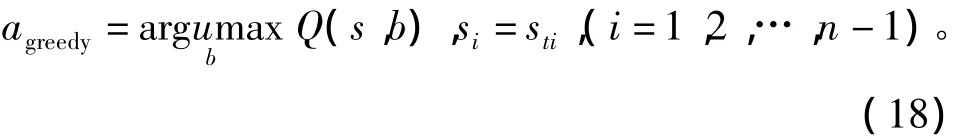
其中b为可选动作。该贪婪动作的求解实际上是一个优化问题，即

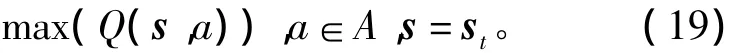
式中A为动作定义域。将当前状态st代入上式有的障碍物与机器人之间的距离。

图2 KheperaⅡ机器人传感器及其布置［10］Fig．2 The displace of the sensor of the robot KheperaⅡ

上述优化问题可以用PSO或GA算法或最简单的格点法进行求解。

为平衡强化学习中特有的搜索和利用两难问题，贪婪动作并不直接作用于环境，而是在其上叠加一个干扰动作ad［15］，即执行动作aexe为

而干扰动作ad服从如下的正态分布:

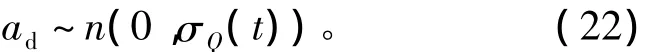
式中

λ为比列因子。

2 沿墙导航

和文献［10］一样，用 Khepera 2［16］机器人仿真器进行实验，该机器人的结构如图2所示，该机器人有6对红外传感发射、接收器，用于测量相应方向上

实验目的是希望机器人在没有任何先验知识的情况下通过强化学习获得一个能控制机器人按顺时针方向沿墙绕行的控制器，因此只需考虑s0，s1，s2，s3这四个传感器的输出作为机器人状态。机器人的动作为转角。将距离进行归一化处理后，机器人离墙的最小距离为0.15 m，最大距离为0.85 m。以传感器s0的测量值为机器人与墙的距离。

仿真实验环境如图3所示。在这个环境中，有三个90°拐角，一个270°拐角，一个 116.57°钝角拐角，一个63.43°锐角拐角，可见该环境比文献［10］要复杂。实验中4个传感器的最大分辨率为1 m，最小分辨率为0.5 m。输出转角在－30°和30°之间，其最大分辨率为60°，最小分辨率为30°。所有分辨率衰减因子均为0.82。TD误差阈值eT为0.01，TD误差计算式（2）中的折扣因子γ=0.48，Q值更新式（1）中学习因子α=1。重叠因子τ=0.82。卡尔曼滤波器参数P0=R0=1.0，Q0=0.000 5。式（23）中λ=0.4。机器人速度为0.2 m/s。机器人决策时间间隔为200 ms。为简单起见，贪婪动作及最大Q值的计算采用格点法，即按ai=－30°+i+f（i=0°，1°…，60°，f是一个在区间［－0.5，0.5］上服从均匀分布的随机数。如果ai大于30°，取ai为30°，如果ai小于 －30°，取ai为 －30°）。比较60 个输出动作的Q值，取Q值最大的动作为贪婪动作。

强化信号定义为

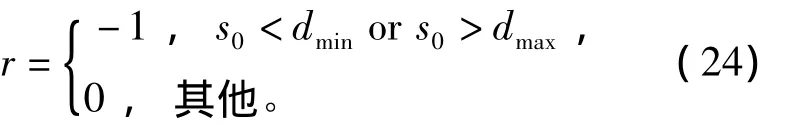
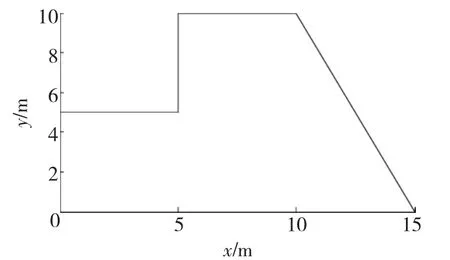
图3 仿真环境Fig．3 The enviroment of simulation

为加快学习速度同时减小计算量，采用经验重放的方法［17］进行学习。

一次运行中最大尝试次数为500，当机器人能绕墙成功行走1 200步（1 200步能确保机器人绕墙至少一周）就视为学习成功。每次尝试时机器人的初始位姿为（0.5，0.5，90°）。

在25次运行中，每次机器人都能经过不到500次尝试就能完成绕墙至少一周的任务。平均尝试次数为67.6，最大尝试次数为480，最小尝试次数为5。控制器平均规则数为14，最大为40，最小为8。性能优于文献［10］的DFQL方法。如果直接采用文献［13］中的方法进行规则增加，即取总的最大分辨率为1，最小分辨率为0.5，在500次尝试中并不能次次成功，同时由于规则数过多，计算量大。

图4给出了在学习成功后绕墙行走的轨迹，该轨迹起点为（0.5，0.5）出发，绕墙一周后终点为（2.66，4.42）。在这次运行中，控制器经过9次尝试后就能成功地控制仿真机器人实现沿墙行走。

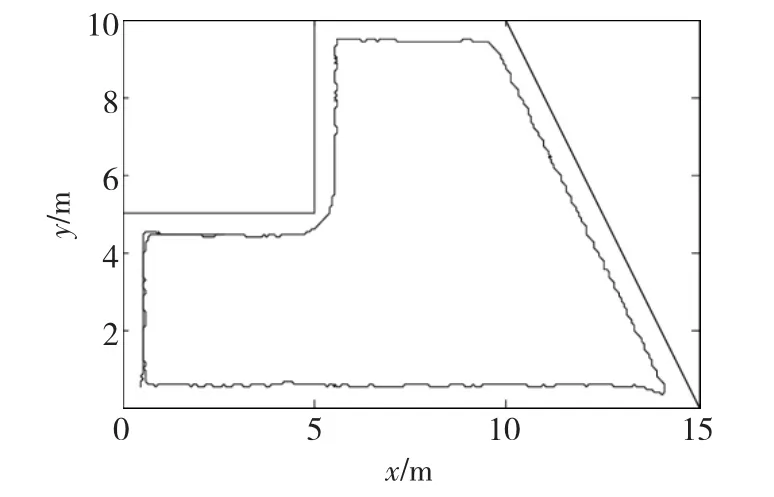
图4 机器人绕墙行轨迹Fig．4 The tragectory of the robot

图5给出了机器人方向角的变化情况，图6给出了控制器在1 200步的沿墙运动中输出的控制量变化。图7所示为每个传感器在沿墙行走过程中的测量值。图8给出了在学习后自动建立的9条规则中每个输入变量隶属度函数。

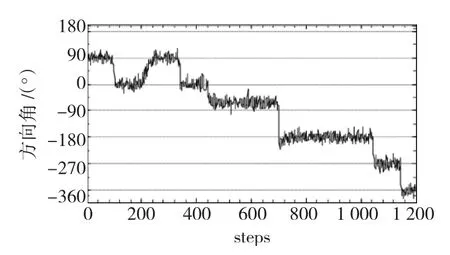
图5 机器人方向角变化曲线Fig．5 The azimuth of the robot

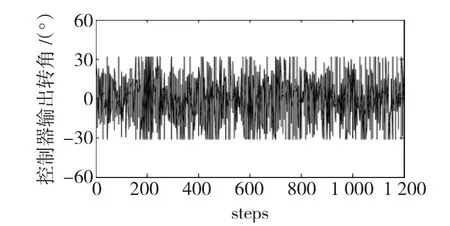
图6 控制器输出控制量Fig．6 The output of the controller

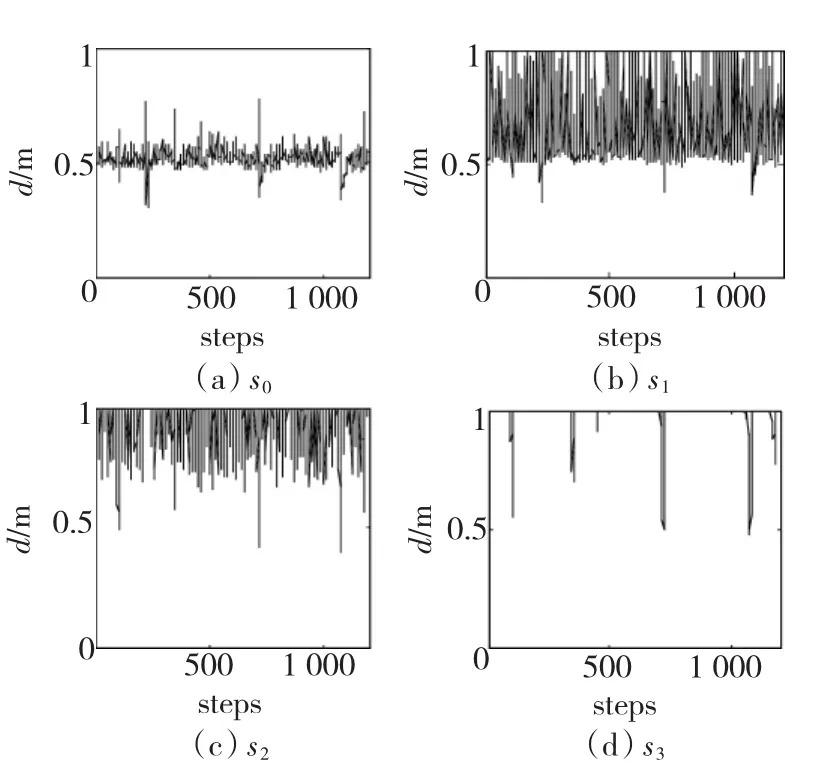
图7 各传感器测量值变化Fig．7 The sensors value during moving

图8 各输入变量的隶属度函数曲线Fig．8 Member function of ench variable

在25次运行过程中，一旦控制器通过学习能控制机器人过90°拐角和270°拐角后，就可以直接过116.57°钝角拐角，这说明该学习系统具有较强的泛化性能。对于63.43°锐角拐角有时还需要进行学习。同时控制器在学习通过拐角的过程中，对沿直线墙行走控制一般没有影响，这源于FRBF网络具有局部逼近的特性。

从图5的机器人方位角变化情况来看，机器人在直线段行走过程中，方向角总的来说是以墙的方向角为基准波动，这种波动一是由于强化学习中已有知识的应用和新知识的探索之间的平衡所致。为能搜索到更好的策略，学习主体每次执行的动作并非是最优动作（已有知识的利用），通过选择贪婪动作之外的动作来发现更好的动作（搜索），但这将会导致系统性能下降。二是由于传感器s0的测量值并非是机器人和墙之间的距离，传感器的测量值对机器人的姿态非常敏感，姿态的细微变化会导致测量值的巨大波动，为克服这种测量波动，机器人基本上是以一种之字形的路线沿墙行走，以保持其不出“轨道”。这一点从图6控制器输出控制量变化情况也可以看出。尽管传感器s0的测量值不是机器人与墙的真正距离，用本文所提的方法仍然能获得一个可以控制该机器人实现沿墙行走的控制器。

图7和图8分别给出机器人在1 200步的运行过程中四个传感器输出的测量数值和状态动作对的五个分量的八个语言变量的隶属度函数。

在前面所述文献中，如文献［10］，控制器的输出动作总的来说是基于预先选定的若干个离散的加权构成，假设离散种子动作集合B={a1，a2，…，am}，规则数为n，则控制器输出动作为

其中bi为第i条规则输出动作，βi为第i条规则后件。将上式进行如下处理并按ai进行同类项合并，即有:

由上式可见，由离散种子动作加权获得输出动作本质上是由种子动作构成的向量和由规则后件构成的向量的内积，后者需要通过学习来确定，其参数空间的维数为m－1。为获得连续的动作，离散动作数m一般都取得较大，如在文献［10］中，m为13，这样参数空间维数比原来动作空间维数要大，因此学习速度慢，且同一规则内的离散动作之间没有泛化能力。

3 结论

本文提出了一种基于模糊Q-学习导航控制方法，与已有的连续空间中的Q学习方法相比，其特点之一是以模糊神经网络对Q值函数进行直接逼近，通过函数优化的方法获得输出动作，这就克服了相关文献中种子动作的选择问题，实现了强化学习和函数优化技术的结合。特点之二是提出了一种新的模糊规则自适应构造方法，实现了在学习过程中模糊规则的自动构建和相关参数的自适应调整，避免了模糊规则手工建立的困难。此外学习经验不但能在邻近的状态中可以进行泛化，还可以在相邻的动作之间进行泛化，因此学习速度也得到提高。实验结果表明该方法可以成功实现机器人沿墙行走的导航控制。

今后还将该方法应用到其他控制问题，此外本文所提的模糊规则自适应方法还可以应用到监督学习等方面，这都是今后的研究内容。

［1］ TURENNOUT P，HONDERD G，SCHELVEN L J．Wall-following control of a mobile robot［C］//Proceedings of the1992IEEE International Conference on Robotics and Automation，May 12 － 14，1992，Nice，France．1992:280－285．

［2］ BORENSTEIN J，KERON Y．The vector filed histogram fast obstacle avoidance for mobile robots［J］．IEEE Transactions on Robotics and Automation，1991，7（3）:278－288．

［3］ 彭一准，原魁，刘俊承，等．室内移动机器人的三层规划导航策略［J］．电机与控制学报，2006，10（4）:380－384．

PENT Yizhun，YUAN Kui，LIU Juncheng，et al．A three-layer planning navigation method for indoor mobile robot［J］．Electric Machines and Control，2006，10（4）:380 －384．

［4］ KHATIB O．Real-time obstacle avoidance for manipulator and mobile robots［J］．International Journal of Robotic Research，1986，5（1）:90－98．

［5］ Lee P S，Wang L L．Collision avoidance by fuzzy logic control for automated guided vehicle navigation［J］．Journal of Robotic Systems，1994，11（8）:743 －760．

［6］ ZHANG Wenzhi，LU Tiansheng．Reactive fuzzy controller design byQ-learning for mobile robot navigation［J］．Journal of Harbin Institute of Technology，2005，12（3）:319 －324．

［7］ 吴洪岩，刘淑华，张嵛．基于RBFNN的强化学习在机器人导航中的应用［J］．吉林大学学报:信息科学版，2009，27（2）:185－190．

WU Hongyan，LIU Shuhua，ZHANGYu．Application of reinforcement learning based on radial basis function neural networks in robot navigation［J］．Journal of Jilin University:Information Science Edition，2009，7（2）:185－190．

［8］ 陆军，徐莉，周小平．强化学习方法在移动机器人导航中的应用［J］．哈尔滨工程大学学报，2004，25（2）:176－179．

LU Jun，XU Li，ZHOU Xiaoping．Research on reinforcement learning and its application to mobile robot［J］．Journal of Harbin Engineering University，2004，25（2）:176－179．

［9］ 段勇，徐心和．基于模糊神经网络的强化学习及其在机器人导航中的应用［J］．控制与决策，2007，22（5）:525－534．

DUAN Yong，XU Xinhe．Reinforcement learning based on FNN and its application in robot navigation［J］．Control and Decision，2007，22（5）:525－534．

［10］ ER M J，DENG C．Online tuning of fuzzy inference systems using dynamic fuzzyQ-learning［J］．IEEE Transactions on Systems，Man and Cybernetics Part B:Cybernetics，2004，34（3）:1478－1489．

［11］ BARTO A G，SUTTON R S，ANDERSON C W．Neuron like adaptive elements that can solve difficult learning control problems［J］．IEEE Transactions on Systems，Man，and Cybernetics，1983，13（5）:834－846．

［12］ LEE C C．Fuzzy logic in control systems:fuzzy logic controller-Part I and II［J］．IEEE Transactions on Systems，Man and Cybernetics，1990，20（2）:404 －435．

［13］ PLATT J．A resource allocating network for function interpolation［J］．Neural Computation，1991，3（2）:213 －225．

［14］ SINGHAL S，WU L．Training multilayer perceptrons with the extended Kalman algorithm［C］//Advances in Neural Processing Systems，December 12 －14，1988，San Mateo，CA．1988:133－140．

［15］KONDO T，ITO K．A reinforcement learning with evolutionary state recruitment strategy for autonomous mobile robots control［J］．Robotics and Autonomous Systems，2004，46（2）:111－124．

［16］ KTEAM S A．Khepera 2 User Manual［R］．Switzerland，2002．

［17］ LIN L J．Self-improving reactive agents based on reinforcement learning，planning and teaching［J］．Maching Learning，1992，8（3－4）:293－321．

（编辑:刘素菊）