Buck变换器动态过程电容充放电平衡控制策略

刘晓东， 蒋昌虎， 邱亚杰， 陈宗祥， 刘雁飞，2

（1．安徽工业大学电气信息学院，安徽马鞍山243002;2．皇后大学电气与计算机工程系，加拿大金士顿K7L3N 6）

0 引言

近年来，DC－DC开关变换器在微处理器如CPU、DSP供电中的应用越来越广泛。在动态时要求供电电压的波动在一个很小的范围内，因此对供电电源动态性能提出了更高的要求。传统的线性控制器（如电压模式控制）稳态误差为零，算法简单。但是因为受到带宽的限制，动态响应效果不甚理想［1］。大信号扰动时，占空比饱和，动态过程就会变得缓慢，不适用于对动态性能要求较高的场合。常用的数字控制策略多比较复杂，很多情况下需要采用数字芯片，成本较高，而且A/D、D/A转换时间也会对动态过程产生影响［2－3］。

文献［5］研究了一种控制算法，即在负载稳定时采用电压控制模式，负载突变时采用基于电容充放电平衡原理的非线性控制，计算出开关管的占空比，得到最优的动态响应过程，且采用常用的模拟器件就可以实现。但是该文献未对负载不同时刻突变的动态过程进行分析［4－5］。

本文对电容充放电平衡控制算法进行了更深入的探讨，以负载电流增大为例，分别对电感电流最大和最小时刻的负载突变进行了理论分析，并推导出了恢复时间和电压欠调量的计算公式，最后用仿真证明理论分析的正确性。

1 非线性动态调节过程

1.1 负载突变调节过程

如图1所示，假定Buck同步整流变换器工作在电流连续状态，且在负载变化过程中，输入电压恒定。图2为线性控制动态调节过程。该线性控制为电压模式控制，在动态过程中开关频率不变，通过调节占空比实现调节过程。当负载电流i突变时，开关管的占空比d随之增大，电路逐渐恢复到稳态［6－7］。图3为本文介绍的非线性控制动态过程，当负载电流突变时，通过计算得到开关管的导通和关断时间，电路的动态特性得到很大改善，在几个开关周期内就可以达到稳态［8］。

图1 Buck同步整流电路图Fig．1 Buck converter with synchronous rectifier

图2 线性控制动态调节过程Fig．2 Dynamic response of linear control

图3 线性－非线性－线性控制动态调节过程Fig．3 Dynamic response of linear－nonlinear control

1.2 非线性控制切换

基于电容充放电平衡控制算法的Buck变换器在稳态时采用线性控制，动态时采用非线性控制。控制模式选择信号是由检测到的电容电流与设定阈值比较得到的。理论上，当检测到电容电流大于其纹波峰值时即可切换到非线性控制，在运行到新稳态时再选择线性控制。本控制算法在负载电流突变量较大时优越性更明显，在负载电流变化量较小时采用电压模式控制也可以取得与之相仿的动态特性。因此在设定阈值时应留有一定裕量，在保证良好动态特性的前提下简化控制策略。

2 电容充放电平衡算法原理

2.1 电路达到稳态条件

本文以Buck电路负载电流正突变为例，对电容充放电平衡算法进行说明。电路从动态恢复到稳态需要同时满足两个条件［9］:

1）输出电压恢复到参考电压。在Buck电路中电容电压就等于输出电压。由图4可知，输出电压ν的变化是电容的充放电引起的，电容充电时输出电压增大，电容放电时输出电压减少。对于电容满足

式中:Q为电容电量;C为容值;U为电容电压;ΔU为电容电压变化量;ΔQ为电容电荷变化量。

由式（2）可知，输出电压恢复到参考电压，即电容电压变化的代数和为零，需满足电容放电电荷量等于充电电荷量。

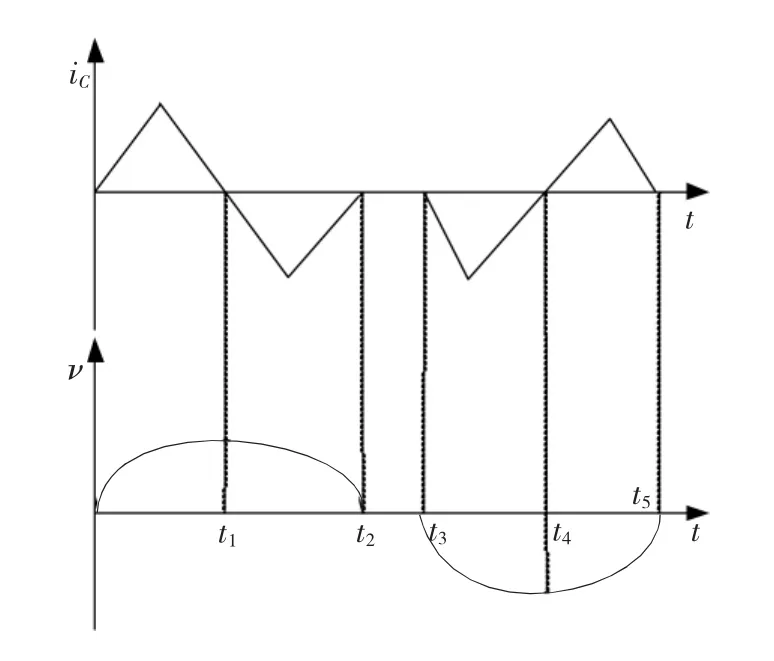
图4 电容电流与电压变化关系Fig．4 The waveform of capacitor current and voltage

2）电感电流等于突变后的负载电流。对于确定的电路拓扑和参数，电感电流变化率也是确定的。通过控制开关的导通和关断时间让其最终值等于新的负载电流［10］。

电感电流上升率m1与下降率m2可表示为

式中:Vo为输出电压;Vin为输入电压;IL为电感电流。

该算法就是通过同时满足以上两个条件来改善动态性能，即通过计算得到动态过程中开关管的导通和关断时间，使电路达到稳态。

2.2 电容充放电平衡控制算法

图5为电容充放电平衡算法下负载电流变大时的动态响应，在t0时刻负载电流发生突变，由于电感电流不能突变，电容对负载放电，输出电压减小。此时控制开关管Q1导通，Q2关断。电感电流跟踪负载电流线性增大。当电感电流增至负载电流，输出电压达到最小值，此后电感电流继续增大，大于负载电流，对电容充电，输出电压开始上升。通过计算得到t2时刻，控制主开关管关断，电感电流开始下降，保证电感电流下降到新到负载电流时电容充放电荷量相等，此时电路恢复到稳态。电路达到新的稳态条件如图（5）所示。

图5 电容充放电平衡控制下负载电流变大时的响应Fig．5 The dynamic response when load current step positively with charge balance control

式中:Adischarge为电容放电电荷量;Acharge为电容充电电荷量;Io2为突变后负载电流。

式（10）表明t0时，对输出电压进行二重积分，在t1时刻对输入电压进行反相二重积分，之后某一时刻二重积分值为零，该时刻即为t2。此时控制开关管关断，电感电流开始减小，在t3时刻等于新的负载电流时，输出电压也恢复到参考值，此时电路达到稳态。

2.3 突变时刻对动态响应的影响

由于电感上的电流纹波，开关周期不同时刻电感电流的瞬时值不同，因此负载突变时电容充放电荷量也不一样，导致动态响应也会区别。

如图6所示，图6（a）为负载在电感电流最小时突变，记为响应1;图6（b）为负载在电感电流最大值时突变，记为响应2。图6中，直线l1的斜率为电感电流上升率，记为m1;l2的斜率为电感电流的下降率，记为m2。

图6 负载变化在开关周期不同相位时的动态响应

Fig．6 The dynamic response when load current steps at different phase of switching cycle

在主电路拓扑和参数都相同的情况下，在电感电流不同瞬时值发生负载突变时，电感电流变化率相同。

几何关系为

式中△ABC和△A1B1C1面积的物理意义分别为电感电流最小和最大突变的电容放电量。又因为突变时刻相同，所以2个三角形相似，即

由于响应1中，当负载电流突变时电感电流最小。响应2中，电感电流最大，所以△ABC的高大于响应2中△A1B1C1的高，即

故2个三角形面积满足

在负载突变量相同的条件下，响应1的放电电荷大于响应2的放电电荷。由电容充放电平衡原理可知，响应1的充电电荷也应大于响应2的充电电荷。

由图6可以直观地看出

即响应2比响应1先达到稳态。

电容在T0期间处于放电状态，输出电压减小，在t1时刻达到最小值。假设t0=0，则

由式（26）、式（27）易知响应2的输出电压欠调量比响应1的输出电压负调量小。

同理当负载电流在电感电流最大和最小发生负跃变，在电感电流最小时突变的动态性能比其他时刻的动态性能都好。图7为电容充放电平衡控制实现框图。

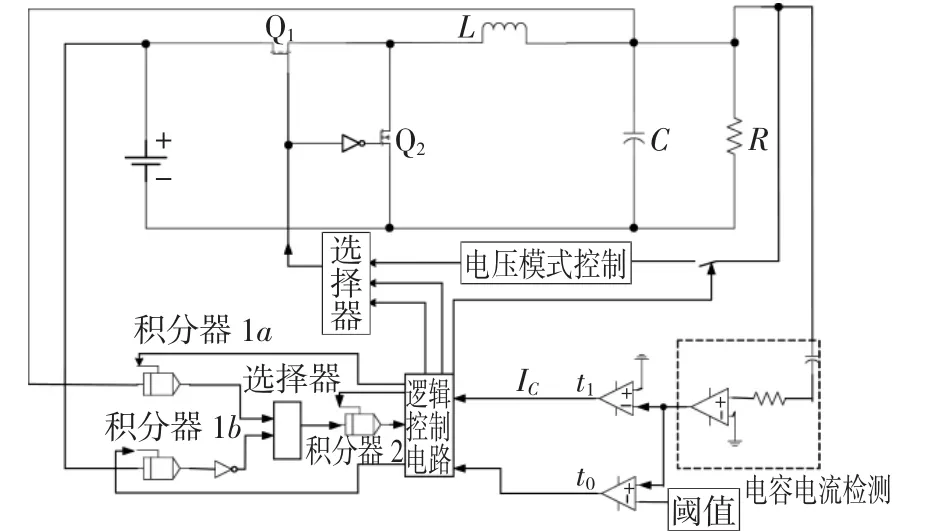
图7 电容充放电平衡控制实现框图Fig．7 Block diagram of capacitor charge balance control

3 仿真结果及分析

在PSIM软件中，对电容充放电平衡控制和电压模式控制进行仿真，仿真结果如图8～图13所示。Buck主电路参数为:Vin=12 V;Vo=1.5 V;fs=400 kHz;L=2.65 μH;C=181 μF;RESR=0.5 mΩ。

图8 电压模式控制下电感电流最小值时负载电流为9～15 A的电感电流和输出电压波形Fig．8 The waveform of output voltage and inductor current when load current step from 9 A to 15 A at the minimum of inductor current with voltage mode control

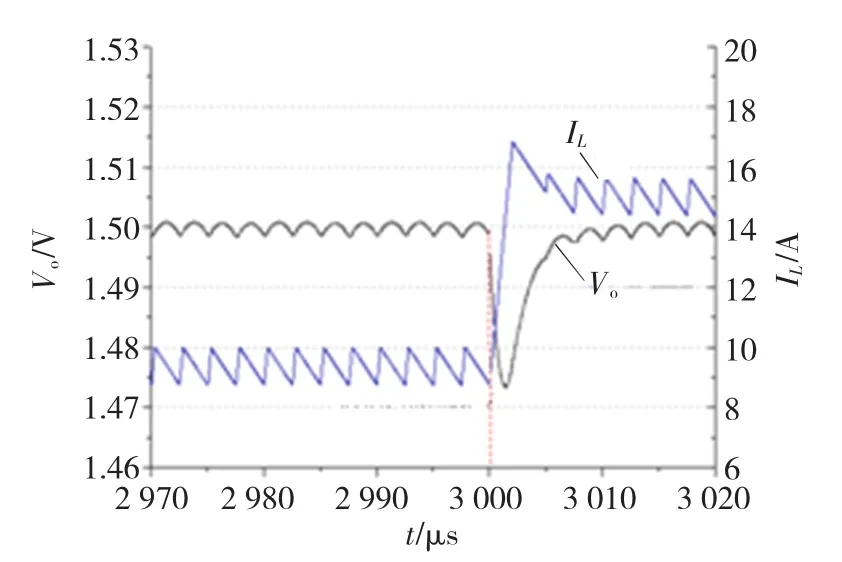
图9 电容充放电平衡控制下电感电流最小值时负载电流为9～15 A的电感电流和输出电压波形Fig．9 The waveform of output voltage and inductor current when load current step from 9 A to 15 A at the minimum of inductor current with charge balance control

图10 电容充放电平衡控制下电感电流最大值时负载电流为9～15A的电感电流和输出电压波形Fig．10 The waveform of output voltage and inductor current when load current step from 9 A to 15 A at the maximum of inductor current with charge balance control

图11 电压模式控制下电感电流处于最小值时负载电流由9.5 A变化到6.5 A的电感电流和输出电压波形Fig．11 The waveform of output voltage and inductor current when load current step from 9.5 A to 6.5 A at the minimum of inductor current with voltage mode control

图12 电容充放电平衡控制下电感电流最小值时负载电流由9.5 A变化到6.5 A的电感电流和输出电压波形Fig．12 The waveform of output voltage and inductor current when load current step from 9.5 A to 6.5 A at the minimum of inductor current with charge balance control

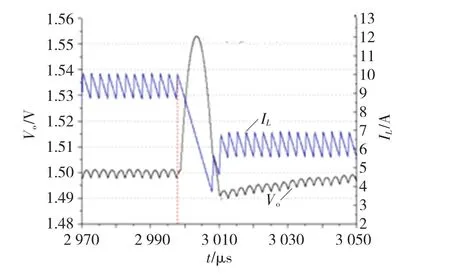
图13 电容充放电平衡控制电感电流最大值时负载电流由9.5 A变化到6.5 A的电感电流和输出电压波形Fig．13 The waveform of output voltage and inductor current when load current step from 9.5 A to 6.5 A at the maximum of inductor current with charge balance control

图8～图10分别为电压模式控制和电容充放电平衡控制下负载电流增大时的仿真波形。电容充、放电平衡算法的动态性能明显优于电压模式控制的动态性能，动态性能指标（电压欠/超调量和恢复时间）得到很大改善。由图9、图10的对比可知，负载电流增大时在电感电流最大值时刻突变的动态性能要优于最小值时刻的动态性能。输出电压欠调量从25 mV减小到17 mV，恢复时间从8 μs减小到5 μs。

同理，由图11～图13的对比可知，电容充、放电平衡控制具有良好的动态特性，并且负载电流减小时电感电流最小值时刻的动态性能要优于最大值时刻的动态性能。前者输出电压超调量为46 mV，恢复时间为12 μs。后者输出电压超调量和恢复时间分别为 53 mV、12.5 μs。

仿真结果对前面理论分析进行了验证，即采用电容充放电平衡控制，负载电流正突变时，在电感电流最大值时动态性能最好。负载电流减小时，发生在电感电流最小值时动态性能最好。

4 结语

本文对采用电容充放电平衡控制Buck变换器动态特性进行了研究。以负载电流增大为例，对电感电流最大和最小时刻负载突变过程进行了分析。分析表明电感电流不同值时发生突变其动态响应不相同，电感电流最大时发生正跳变具有最好的动态特性，最小时动态特性最不理想。仿真结果验证了理论分析的正确性，同时表明与传统电压模式控制相比，在动态过程中采用电荷充放电平衡控制输出电压欠/超调量和动态调节时间有显著改善，该算法也可以应用于Boost、Buck-Boost等变换器。

［1］FENG G，MEYER E，LIU Y F．A digital two-switching-cycle compensation algorithm for input-voltage transients in DC-to-DC converters［J］．IEEE Transactions on Power Electronics，2009，24（1）:181－191．

［2］ CASTILLA M，DE VICUNA L G，GUERRERO J M．Simple lowcost hysteretic controller forsingle-phase synchronous Buck converters［J］．IEEE Transactions on Power Electronics，2007，22（4）:1232－1241．

［3］ ERSHADI M H，POUDEH M B，ESHTEHARDIHA S．Fuzzy logic controller based genetic algorithm on the step-down converter［C］//2008International Conference on Smart Manufacturing Application，April 9 － 11，2008，Gyeonggi-do，Korea．2008:324－328．

［4］ YOUSEFZADEH V，BABAZADEH A，RAMACHANDRAN B，et al．Proximate time-optimal digital control for synchronous buck DC-DC converters［J］．IEEE Transactions on Power Electronics，2008，23（4）:2018 －2026．

［5］ MEYER E，ZHANG Z L，LIU Y F．An optimal control method for Buck converter using a practical capacitor charge balance technique［J］．IEEE Transactions on Power Electronics，2008，23（4）:1802－1812．

［6］QIU Yajie，JIANG Changhu，LIU Xiaodong，et al．The optimal control in dynamic state for DC-DC converters［C］//CPSSC’2009，November 13－16，2009，Xiamen，China．2009:403 －405，398．

［7］ 马红波，洪全源．BUCK型开关变换器最优PID控制器设计［J］．电机与控制学报，2008，12（6）:639 －643．

MA Hongbo，FENG Quanyuan．Optimized PID controller design for buck DC-DC switching converter［J］．Electric Machines and Control，2008，12（6）:639 －643．

［8］ 华晓辉，林维明，熊代富．DC/DC变换器快速动态响应分析［J］．电力电子技术，2007，41（1）:83 －85．

HUA Xiaohui，LING Weiming，XIONG Daifu．Analysis of fast transient response in DC/DC converters［J］．Power Electronics，2007，41（1）:83－85．

［9］ 吴忠强，王志君．DC/DC变换器的一种无源化控制方案［J］．电机与控制学报，2008，12（2）:147 －150．

WU Zhongqian，WANG Zhiju．Kind of passivity control scheme for DC/DC converters［J］．Electric Machines and Control，2008，12（2）:147－150．

［10］ 张占松，蔡宣三．开关电源的原理与设计 ［M］．北京:电子工业出版社，2004:55－90．

（编辑:张诗阁）