The interconnected stability and cooperative control for a class of uncertain time-delay systems

ZHAO Hui， CHEN Dong-yan， HU Jun

（Department of Applied Mathematics，Harbin University of Science and Technology，Harbin 150080，China）

0 Introduction

A large-scale dynamical system is generally characterized by a large number of variables representing the system．Considerable research attention has been devoted to the decentralized control theory，which is a basic method for addressing large scale system，and many results have been reported，see［1－6］and the references cited therein．Some special decentralized control problems are studied for discrete-time interconnected systems in ［4］and ［5］．It has been shown that some unstable subsystems can generate a stable system under effective interconnections．Recently，stability analysis and decentralized control problems are addressed for a class of complex dynamical networks in［6］．Some criteria for stability and stabilization under a special decentralized control strategy are established for networks by using a simple similarity transformation．

Recently，a series of significant results on interconnections and cooperative control of linear or nonlinear systems have been presented［3，5，7－9］．The interconnected stability and cooperative control of largescale linear systems are investigated in ［9］．Necessary and sufficient conditions for interconnected stability and cooperative stabilization of two independent subsystems are presented by using the BMI technique，and the problems of designing interconnection matrices and cooperative controllers are converted into corresponding optimization problems．It is well known that time-delays are frequently encountered in a variety of industrial and engineering systems．The existence of time-delay may cause undesirable dynamic network behaviors such as oscillation and instability．It worth mentioning that the time-delay case was not discussed in ［9］，then there is much room for further investigating．

On the other hand，convex polytopic uncertainties have the properties of natural and more universal and less conservative than norm-bounded uncertainty on describing practical problems［10］，and have been received considerable attention from researchers and a large number of related results have been obtained［11］．

Motivated by the above discussion，in this paper，we deal with the interconnected stability and cooperative control of linear uncertain time-delay subsystems with convex polytopic uncertainty by using the LMI and BMI techniques．Firstly，a sufficient condition for the interconnected stability of uncertain time-delay subsystems with convex polytopic uncertainty is presented．In addition，we consider the optimization designing problem of the interconnection matrices，and give a sufficient condition for interconnected stability such that certain performance index of uncertain time-delay subsystems with convex polytopic uncertainty is satisfied．Secondly，we investigate the stabilizing problem of given uncertain time-delay subsystems through cooperative controllers．Thirdly，optimization algorithms based on the BMI are presented，and a numerical example is given to demonstrate the validity of the presented result．Finally，we conclude this paper．

Notations．The notations used throughout the paper are standard．Matrices are denoted by capital letters and scalars are denoted by lowercase Greek letters．The superscript‘T’stands for matrix transposition;Rndenotes then-dimensional Euclidean space．I and 0 represent the identity matrix and a zero matrix with appropriate dimensions．‘diag{…}’stands for a block-diagonal matrix．Matrices，if there dimensions are not explicitly stated，are assumed to be compatible for algebraic operations．

1 The interconnected stability and guaranteed cost of linear uncertain timedelay subsystems

Consider the following two independent linear uncertain time－delay subsystems:

where xi（t）∈Rni，i=1，2 are the states of subsystem;Ai，Aiτ∈Rni×ni，i=1，2 are known constant matrices，ΔAi，ΔAiτ∈Rni×ni，i=1，2 are unknown uncertain matrices;τ1andτ2represent the non-negative delays components in the states;φi（t），i=1，2 are the initial functions on the segment［－ τi，0］．

Suppose that uncertain matrices ΔAiand ΔAiτ，i=1，2 are not precisely known，but belong to a convex bounded uncertain domain given by

where Eijiand Filiare known constant matrices．

We are in the position to state the problem to be addressed in this section as follows．

Problem 1:For all the unknown uncertain matrices ΔAiand ΔAiτsatisfying（3），whether there exist interconnected matrices A12∈Rn1×n2and A21∈Rn2×n1and how to design interconnected matrices A12and A21，such that the interconnected uncertain time-delay system

is asymptotically stable，as well as the optimization problem for designing interconnected matrices A12and A21under the following performance index

Here，x（t）= ［x1（t），x2（t）］T，Ad=diag{A12，A21}，and Q is a known symmetric semi-positive definite matrix．

Definition 1 If there exist matrices A12and A21，such that the interconnected uncertain time-delay system（4）is asymptotically stable for all the unknown uncertain matrices ΔAiand ΔAiτsatisfying（3），then the uncertain time-delay subsystems（1）and（2）are said to be interconnected stable．

Setting

then the interconnected uncertain time-delay system（4）can be rewritten as follows

We are in the position to derive a sufficient condition under ensuring the uncertain time-delay subsystems（1）and（2）to be interconnected stable for all parameter uncertainty satisfying（3）．

Theorem 1 The uncertain time-delay subsystems（1）and（2）is interconnected stable，if there exist symmetric positive definite matrices P11，P22，S11，S22，R11，R22，and matrices P12，S12，R12，A12，A21，R12，A12such that the following matrix inequalities（7）～（10）hold，According to the Lyapunov stability theory，if there exist symmetric positive definite matrices P，S and R，such that the following inequality holds，then the system（6）is asymptotically stable．Note that，inequality（12）can be expressed as follows

Hence，it follows from（10）that（13）holds．This completes the proof．

Remark 1 Note that the inequalities（7）－（9）are LMIs and inequality（10）is a BMI，the solution of Theorem 1 can be converted into a problem of find the global solution to the following optimization problem（P1）:

Now，weconsidertheoptimization designing problem of the interconnected matrices．

Theorem 2 If there exist symmetric positive definite matrices P11，P22，S11，S22，R11，R22，and matrices P12，S12，R12，A12，A21，such that LMIs（7）～ （9）and the following BMI

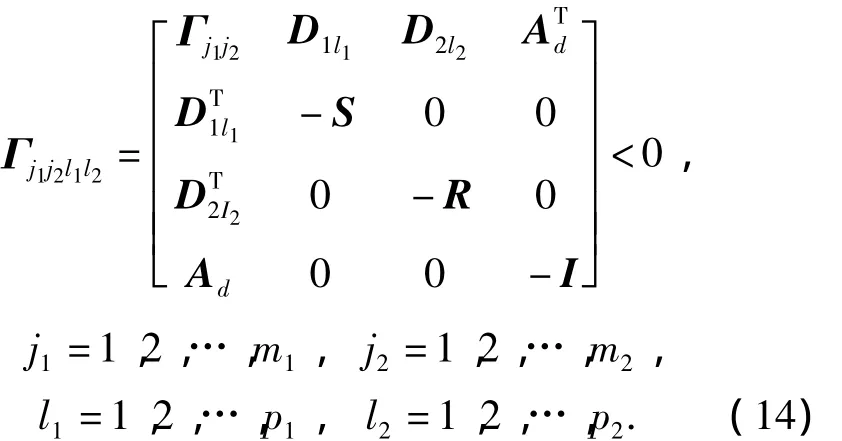
and then the uncertain time-delay subsystems（1）and（2）can be interconnected stable by interconnection matrices A12and A21．The performance index（5）satisfies the following inequality:

ProofFor the interconnected uncertain time-delay system（6），we choose a Lyapunov function as（11）．Then，along the solution of system（6），the time derivative ofV（x（t））is given by

Therefore，the interconnected uncertain time-delay system（6）is asymptotically stable．

Furthermore，integrating both sides of（17）from 0 toT，and noting the initial condition，we have

Then，we obtain inequality（15）．

On the other hand，together with the Schur complements，inequality（16）is equivalent to the following inequality:

Similar to the proof of Theorem 1，inequality（18）holds if the BMI（14）holds．This completes the proof．

According to Theorem 2，the optimization problem for designing interconnection matrices A12and A21can be formulated as:

2 Optimization design of the cooperative controllers for linear uncertain time-delay subsystems

In this section，we consider the stabilized problem of given uncertain time-delay subsystems through cooperative controllers．

Consider the following two independent linear uncertain time-delay subsystems:where u12（t）∈Rm1and u21（t）∈Rm2are cooperative control variables，B12∈Rn1×m1and B21∈Rn2×m2are known constant matrices，other symbols are the same as those in the above section．

In this section，we consider the following problem．

Problem 2:For all the unknown uncertain matrices ΔAiand ΔAiτ（i=1，2）satisfying（3），whether there exist state feedback controllers（i．e．，cooperative controllers）

u12（t）=K12x2（t），u21（t）=K21x1（t）， （23）such that the following closed-loop interconnected uncertain time-delay system

is asymptotically stable，as well as the optimization problem for designing cooperative controllers（23）under the following performance index

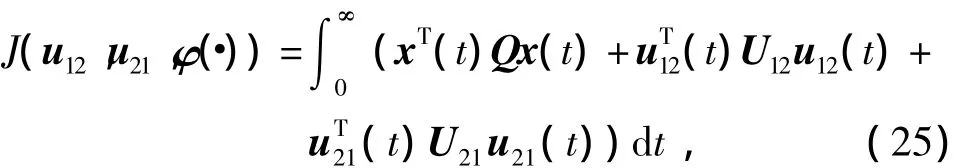
where U12∈Rm1×m1and U21∈Rm2×m2are given symmetric positive definite matrices，K12∈Rm1×n2and K21∈Rm2×n1are unknown constant matrices to be designed．

Definition 2If there exist cooperative controllers（23），such that the closed-loop interconnected uncertain time-delay system（24）is asymptotically stable for all the unknown uncertain matrices ΔAiand Δ Aiτ（i=1，2）satisfying（3），then the uncertain time-delay subsystems（21）and（22）are said to be cooperatively stable．

The following theorem presents a sufficient condition underwhich uncertain time-delay subsystems（21）and（22）are cooperatively stable through cooperative controllers（23）．

Theorem 3If there exist symmetric positive definite matrices P11，P22，S11，S22，R11，R22，and matrices P12，S12，R12，K12，K21，such that inequalities（7）～（9）and the following matrix inequality

Then the uncertain time-delay subsystems（21）and（22）can be cooperatively stable，and state feedback controllers（23）are said to be cooperative controllers．where

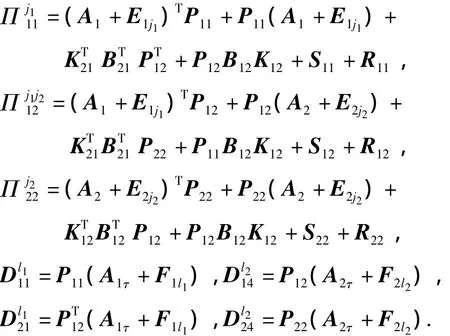
ProofTo prove this theorem，we only need to replace A12and A21with B12K12and B21K21in Theorem 1．The proof is complete．

Theorem 3 can be obtained by solving the following optimization problem:

Theorem 4If there exist symmetric positive definite matrices P11，P22，S11，S22，R11，R22，matrices P12，S12，R12，K12，K21，such that the LMIs（7）～ （9），and the following BMI

Then subsystems（1）and（2）can be cooperatively stable by cooperative controllers（23），and the performance index（25）satisfies the following inequality:

ProofTo prove this theorem，we only need to replace A12and A21with B12K12and B21K21in Theorem 2．The proof is complete．

By Theorem 4，the optimization methods for designing cooperative controllers（23）can be formulated as:

3 Optimization algorithm based on BMI

The optimization（P1）is a feasible problem of the LMI and BMI．Since inequality（10）is a BMI with variable Pij，i，j=1，2 and A12，A21，if fix Pij，i，j=1，2，BML（10）can be formulated as LMI in matrix variable A12，A21，and if fix A12，A21，BML（10）can be formulated as LMI in matrix variable Pij，i，j=1，2．Therefore，we can present the following algorithm to solving optimization problem（P1）．

Optimization problem（P2）is a standard generalized eigenvalue problem（GEVP）with LMI and BMI constraints，the process of solving it can be finished in two steps．The first step is to obtain the feasible solution（P（0），S（0），R（0），A（0）12，A（0）21）of LMIs（7）～ （9）and BMI（10）by using the same methods as Algorithm 1;the second step is to use the following optimization algorithm 2．

It can be noted that if A12，A21are fixed，optimization（P3）is a standard GEVP problem with LMI constraints．It has been proved that the existence and the uniqueness are satisfied for optimal solution to such optimization problems．

Only the replacement of A12and A21with B12K12and B21K21，respectively，in Algorithm 1 and Algorithm 2 is required to solve the（P4）～（P6）．

4 A numerical example

We consider the following two independent subsystems·

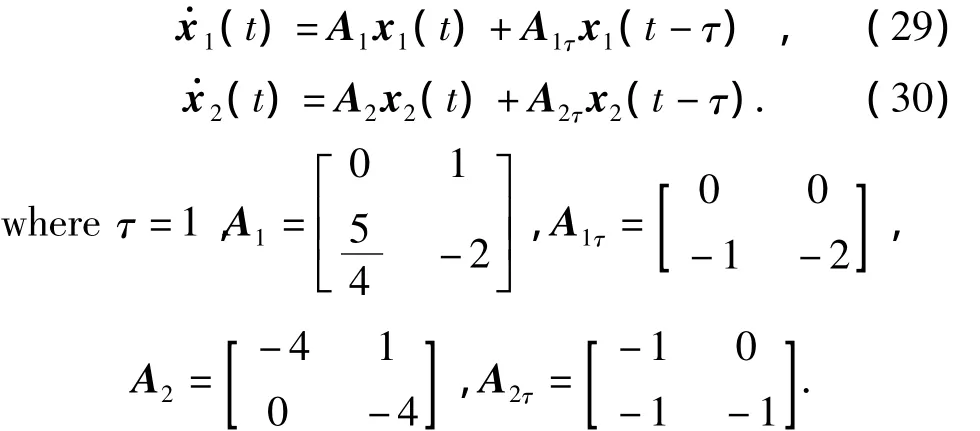
It is easy to determine that the subsystem（29）is unstable，but the subsystem（30）is stable．We shall stabilize the subsystems by the method of interconnected stability．Here，the inequality（10）in Theorem 1 becomes to

is stable．The curves of systems above are given as follows．

The simulation results are shown in Figs．1 － 3 which imply that the desired goal is well achieved．

Fig．1 state response of subsystems（29）

Fig．2 state response of subsystem（30）

Fig．3 state response of interconnected system（34）

5 Conclusion

This paper discusses the problem of interconnected stability and cooperative control for linear time-delay subsystems with convex polytopicuncertainty．Based on the technique of linear matrix inequality（LMI）and bilinear matrix inequality（BMI），we present several sufficient conditions for the interconnected stability and cooperative control of two independent uncertain time-delay subsystems．The cooperative controllers designing problems can be formulated as a feasible problem with LMI and BMI constraints．In addition，the problem of designing optimal cooperative controller is converted into an optimization problem with LMI and BMI constraints，which can be easily tested by using standard numerical software．The discussion of this paper can be extended to studying the problem of interconnected stability and cooperative control for more independent uncertain time-delay subsystems

［1］ WANG S H，DAVISON E J．On the stabilization of decentralized fixed modes for interconnected systems［J］．Automatica，1983，19（2）:473－478．

［2］ YAND G H，WANG J L．SOH Y C．Decentralized control of symmetric systems ［J］．Systems＆Control Letters，2001，42（2）:145－149．

［3］ DUAN Z S，WANG J Z，HUANG L．Special decentralized control problems and effectiveness of parameter-dependent Lyapunov function method ［C］//Proceedings of American Control Conference．Portland，USA．2005:1697－1702．

［4］ DUAN Z S，WANG J Z，HUANG L．Special decentralized control problems in discrete-time interconnected systems composed of two subsystems［C］//Proceedings of the25th Chinese Control Conference，August 7 －11，2006，Harbin，China．2006:1080 －1085．

［5］ DUAN Z S，WANG J Z，HUANG L．Special decentralized control problems in discrete-time interconnected systems composed of two subsystems［J］．Systems and Control Letters，2007，56（3）:206－214．

［6］ DUAN Z S，WANG J Z，CHEN G R，et al．Stability analysis and decentralized control of a class of complex dynamical networks［J］．Automatica，2008，44（4）:1028 －1035．

［7］ DUAN Z S，HUANG L，WANG J Z，et al．Harmonic control between two systems［J］．Acta Automatica Sinica，2003，29（1）:14－22．

［8］ YANG Y，DUAN Z S，HUANG L．Design of nonlinear interconnections guaranteeing the absence of periodic solutions ［J］．Systems and Control Letters，2006，55（4）:338 －346．

［9］ NIAN X H，CAO L．BMI approach to the interconnected stability and cooperative control of linear systems［J］．Acta Automatica Sinica，2008，34（4）:438－444．

［10］ 王广雄，李连锋，王新生．鲁棒设计中参数不确定性的描述［J］．电机与控制学报，2001，5（1）:5 －7．

WANG G X，LI L F，WANG X S．The description of the parameter uncertainty for robust design ［J］．Electric Machines and Control，2001，5（1）:5 －7．

［11］ 王常虹，奚伯齐，李清华，等．网络化控制系统鲁棒L2－L∞控制器设计［J］．电机与控制学报，2010，14（2）:25－30．

WANG C H，XI B Q，LI Q H，et al．Robust L2－L∞controller design for networked control systems ［J］．Electric Machines and Control，2010，14（2）:25－30．

（编辑:于智龙）