碳素钢在不同应力作用下的漏磁场分布特征❋

李新蕾,任尚坤,任吉林,付任珍,宋 凯

(南昌航空大学无损检测技术教育部重点实验室,江西南昌 330063）

作为一种新的无损检测技术磁记忆检测技术因具有能及时发现构件上的应力集中部位,操作简单,不需要对构件表面作特殊清理,便于现场使用等优点,受到了广泛的关注[1].该方法是基于铁磁材料的力磁效应的应用,利用构件在工作载荷和地磁场的作用下其内部会发生磁畴组织定向和不可逆的重新取向,在应力集中区形成漏磁场.通过检测漏磁场,并结合被检构件的实际运行条件来确定构件表面或近表面的以应力集中为主要特征的早期损伤部位[2-5].目前,对力磁效应的基本规律及机理的理解还没有统一的定论,还处于探索之中.力磁效应规律的本质是应力引起试样的磁化规律,即是试样的磁化强度随应力的变化关系.在本次实验中,通过漏磁场的变化规律来反映试样磁化强度的变化.

1 拉伸实验

以同应力梯度的 45# 钢边缘缺口试样为研究对象,试样的尺寸如图1所示,试样厚度为 2mm,分为 A,B,C三组,各组参数如表1所示.考虑到加工过程中产生的残余应力,所有试样均进行了退火,以消除残余应力的影响.

在室温条件下采用 WDW-E100D型电子程控实验机对试样进行拉伸实验,加载速率为0.2 mm/min;对漏磁场的测量采用的是美国Lakeshore公司生产的弱磁场测量仪 Lakeshore 421,其分辨率为 0.001 Gauss,精确度±0.25%,用于精确测量试样表面的漏磁场.实验过程测量路径为试样中线处长 60 mm的直线,如图1所示.

图1 试样尺寸示意图Fig.1 Geometry of specimen and measu ring line

实验开始前,分别测量各试样的初始磁场,以作为对比.在拉伸实验过程中,当试样加载到一定的载荷,沿扫描路径在线测量试样漏磁场分布.

2 有限元分析

表1 试样尺寸参数Tab.1 Dimensions of specimens

通过有限元模拟软件 ANSYS10.0中的静力学分析模块,采用非线性分析的方法,可以得到加载模型的应力分布结果[6].建模采用 Solid65 8节点三维实体单元,该单元具有塑性、蠕变、膨胀、应力强化、拉裂、压碎以及大变形大应变和模拟各向异性等功能.单元材料属性如表2所列.为取得良好的计算结果并节约计算机资源,人工控制有限元的网格划分,图2为试样的有限元模型.

在静力学分析中,对模型一侧端面施加位移约束,另一端面施加拉应力载荷,位移约束和拉应力载荷位置会自动地转化到相应的节点上,B组试样加载到 0.5 kN,5 kN,7 kN时的应力分布结果如图3所示.从图3可以看出,中线上(即磁场扫描路径)的最大应力并非出现在正对 V形缺口处,而是在 V形缺口两侧的 O形区,随着载荷的增大,最大应力分布区向中间移动.

图4为在 POST1模块提取的试样中线上的应力数据(在 ANSYS中 SX,SY,SEQV分别代表 X方向应力、Y方向应力以及等效应力).由于材料在 X方向受到均匀拉应力 S0作用时,在 V形缺口处将同时产生拉应力 SX与剪切应力 SY,试样处在两者的合力作用下,在试样局部区域开始形成与拉伸轴约成 45°的所谓吕德斯带或屈服线,随后再沿试样长度方向逐渐扩展,直至屈服线布满整个试样长度而进入均匀塑性变形阶段[7].

A,B,C三组最小截面处施加的载荷分别为:A(7 kN/20 mm2=350 MPa),B(9.8 kN/28 mm2=350 MPa),C(12.6 kN/36 mm2=350 MPa),虽然施加的载荷大小一样,但是由于各组的应力集中程度不同,各组的应力分布也不同.由图4可得:A组拉应力最小,切应力最大;C组拉应力最大,切应力最小.

表2 45# 钢平板试样的主要材料参数Tab.2 Parameter of steel 45# plate

图2 C组试样的网格分布Fig.2 Finite elementm ode of specim en C

图3 B组试样的 von Mises应力分布等值线图Fig.3 Equivalen t stress distribution of specimen B

图4 扫描路径的应力分布(A组:7 kN;B组:9.8 k N;C组:12.6 kN)Fig.4 Stress distribution of the scan line

3 实验数据分析

3.1 漏磁场分布

图5与图6是 C组试样分别加载至不同状态时漏磁场的空间分布及梯度分布曲线(A组、B组规律相同,已经减去空间初始磁场).尽管由于材料的不均匀性,每个试样的漏磁场分布不尽相同,但通过多个试样的测量,试样在不同加载状态时所反映的规律是相同的:当试样处于弹性阶段,磁场梯度变化不是很明显,且梯度极值点移动,此现象主要与试样的材料组织状态及热处理工艺有关,亦很好的解释了试样在弹性阶段的磁场值零点漂移现象.

图7为各组试样在加载到屈服点 350 MPa时的磁场梯度 K分布规律,通过与图4比较可知,此时漏磁场的梯度分布规律与等效应力的分布规律具有明显的相关性,在应力取得极大值得区域,磁场梯度也取得极值.

当载荷进一步增加,试样进入均匀塑变及不均匀塑变,如图6,450 M Pa,480M Pa时,磁场梯度依然与屈服阶段的变化趋势相近,但当载荷到达 500M Pa时,由于试样已经出现明显的缩颈现象,此时的最大应力区域已经移至中央,磁场梯度值只有一个极值.通过以上分析可以说明漏磁场的梯度分布可以反映构件的应力分布状态.

3.2 磁记忆信号能量特征值

能量既不会凭空产生,也不会凭空消失,它只能从一种形式转化为别的形式,或者从一个物体转移到别的物体,在转化或转移的过程中其总量不变.

根据铁磁学的研究,在没有外应力和外磁场作用时,处于稳定状态的磁晶体内总的自由能为

式中:EK为磁晶各向异性能;Ems为磁弹性能;Eel为弹性能.

在铁磁体受到弹性应力的作用时,会在磁晶体内增加应力能 E e,总的自由能变为[8]

信号能量的定义[13]:对于给定的能量有限连续信号 x(t),在时间间隔 (-T/2,T/2)内的能量为

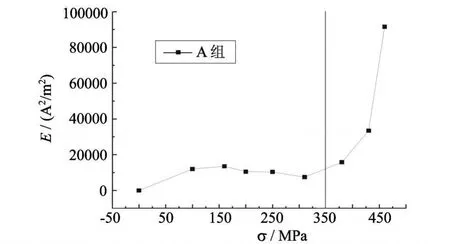
图8 A组试样信号能量随加载状态的变化Fig.8 The signal energy changes w ith stress

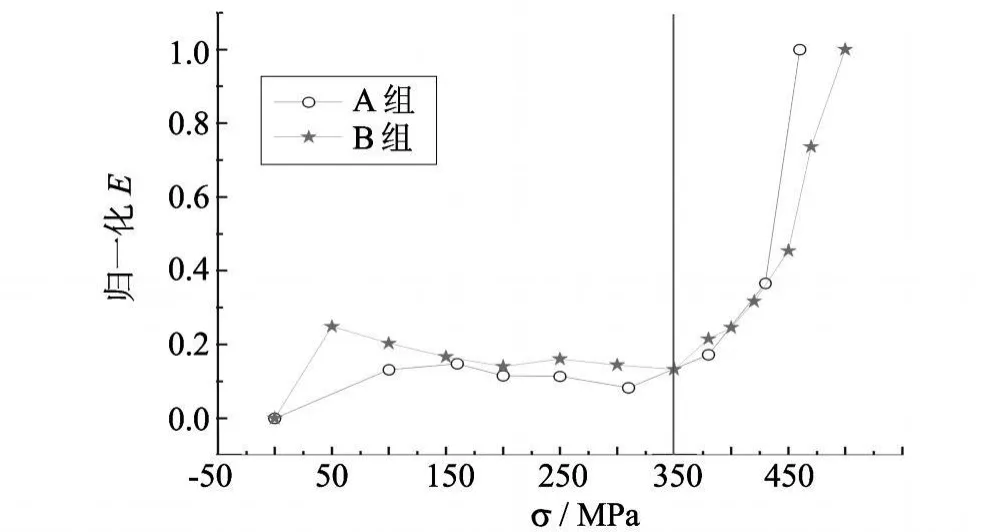
图9 归一化信号能量Fig.9 The normalized signal energy changes with stress

实验中所采集的磁记忆信号是能量有限离散信号,且采集过程匀速扫描,积分由取和代替,故在此定义磁记忆信号的能量为

式中:x0,x1为扫描路径上的两点,为消除漏磁场边缘效应带来的影响,在此分别取 10mm与 50mm做为计算的起点与终点.图8为磁记忆信号能量随加载状态的变化趋势,由图8可知:在弹性阶段,随着应力的增加,磁记忆信号的能量基本保持不变;但是一旦试样过了屈服点进入塑性阶段,磁记忆信号的能量就迅速增加.B组、C组试样具有相同的规律,但是由于应力集中程度的不同,各组试样的磁记忆信号能量大小不尽相同.为此,对磁记忆信号的能量进行归一化处理,如图9所示,可以发现,各组的归一化能量曲线基本重合.我们可以利用磁记忆信号能量这一特征值在屈服点后迅速激增的这一现象,来对构件的受力状态进行检测.

4 结 论

1)应力集中部位与磁场梯度的极值部位具有很好的一致性,故磁场梯度是进行磁记忆检测的有效特征值.

2)磁记忆信号作为一种能量有限信号,可以利用磁记忆信号能量这一特征值在屈服点后迅速激增的现象,来对构件的受力状态进行检测.

[1] 任吉林,林俊明.金属磁记忆检测技术[M].北京:中国电力出版社,2000:1-4.

[2] Dubov A A.Method o fmagnetic memory o fmetals[J].Tyazheloe Mashinostroenie,2003(8):6-7.

[3] Roskosz M,Gaw rilenko P.Analysis of changes in residual magnetic field in loaded notched samp les[J].NDT&E International,2008,41(1):570-576.

[4] Pal'a J,Stupakov O.Magnetic behaviour of low-carbon steel in parallel and perpendicular directions to tensile deformation[J].Journal of Magnetism and Magnetic Materials,2007,310(1):57-62.

[5] Yang En,Li lum ing.Magnetic field aberration induced by cycle stress[J].Journal of Magnetism and Magnetic Materials,2007,312(1):72-77.

[6] 宋凯,唐继红,钟万里,等.铁磁构件应力集中的有限元分析和磁记忆检测[J].材料工程,2004,(4):40-42.

Song Kai,Tang Jihong,Zhong W an li,et al.Finiteelementanalysis andmagneticmemory testing o f ferromagnetism items[J].Journal of Materials Engineering,2004,(4):40-42.(in Chinese)

[7] 束德林.工程材料力学性能[M].北京:机械工业出版社,2003:9-24.

[8] 钟文定.铁磁学(中册)[M].北京:科学出版社 ,1987:21-53.

[9] 任吉林,王东升,宋凯,等.应力状态对磁记忆信号的影响[J].航空学报,2007,28(3):724-728.

Ren Jilin,W ang Dongsheng,Song Kai,et al.In fluence of stress state on magnetic memory signal[J].ACTA Aeronautica Et Astronautica Sinica,2007,28(3):724-728.(in Chinese)

[10] 董丽虹,徐滨士,董世运,等.金属磁记忆技术检测低碳钢静载拉伸破坏的实验研究[J].材料工程,2006(3):40-43.

Dong Lihong,Xu Binshi,Dong Shiyun,et al.Study on metalmagneticmemory signals of low carbon steel under static tension test condition[J].Jouran l o f Materials Engineering,2006(3):40-43.(in Chinese)

[11] 任尚坤,李新蕾,任吉林,等.金属磁记忆检测技术的物理机理 [J].南昌航空大学学报,2008,22(2):11-17.

Ren Shangkun,Li Xin lei,Ren Jilin,et a l.Studies 0n physical mechanism o f metal magnetic memory testing technique[J].Journal o f Nanchang Hangkong University,2008,22(2):11-17.(in Chinese)

[12] 张卫民,刘红光,孙海涛.中低碳钢静拉伸时磁记忆效应的实验研究 [J].北京理工大学学报,2004,24(7):571-574.

Zhang W eim in,Liu Hongguang,Sun Haitao.Magnetic memory effecto f low and medium carbon steel under static tension conditions[J].Transactions of Beijing Institute of Technology,2004,24(7):571-574.(in Chinese)

[13] 张玲华,郑宝玉.随机信号处理[M].北京:清华大学出版社,2003:48-49.