激光超声探测铝板表面微缺陷深度的数值研究❋

关建飞,沈中华,倪晓武,陆 建

(1.南京邮电大学光电工程学院,江苏南京 210046;2.南京理工大学理学院,江苏南京 210094）

0 引 言

利用声表面波检测材料表面缺陷的常规方法主要有基于脉冲回波的测量方法(pulse-echo)[1-2],以及基于衍射模式的渡越时间分析法 (pitch-catch)[3].然而在表面缺陷的深度小于表面波中心波长的情况下,声表面波中的大部分能量将从表面缺陷的底部绕射,这样无论是反射回波信号还是透射表面波位移信号的变化幅度很小以至不易观察.采用这两种传统的方法检测深度小于声波波长的表面缺陷显得十分困难.近年来移动激光源扫查技术 (SLS)[4]作为一种探测表面微缺陷的新技术引起了广泛关注.该技术是采用高功率激光在样品表面聚焦成线源并沿样品上表面垂直于线源长度方向进行扫描.当光源不断靠近表面缺陷直至最后掠过缺陷时(即使缺陷深度小于声表面波的中心波长),在样品上表面的某一固定接收点得到的声表面波位移信号在振幅、峰-峰值乃至频率成分等方面都会发生显著的变化,利用这种显著的变化可以实现对表面微缺陷进行检测.

激光线源具有较大的聚焦面积,可以实现大范围的快速扫描且激发超声的效率较高,同时激发出的声表面波具有方向性好、信噪比高等优点[5],在移动光源检测表面缺陷的技术中,激光线源成为首选的激发源.实验证明 SLS技术不仅不受表面缺陷尺寸的制约,而且缺陷的走向与光源扫描方向的夹角也不会限制该技术的应用.然而采用 SLS技术定量地检测样品表面及亚表面缺陷尺寸就要求明确引起信号幅度等特征变化的物理机理,并建立正确的物理模型来验证这一过程.围绕着这一目的,弹性阵子点阵模型[6]及其与有限差分结合[7],频域边界元法结合 Fourier-Laplace联合变换技术[8]等数值方法都被用来模拟激光源在缺陷近场激发超声波及其传播过程,其结果对探索移动光源扫查技术的物理机理提供了有价值的线索.然而弹性阵子模型将连续介质等效为空间上离散的质点模型,同时每个质点与相邻的八个质点之间通过弹簧相连.这种离散后的简化模型虽然可以近似计算超声波的传播规律,但是由此引入的偏差和伪解也是无法避免的.而积分变换法是应用对时间坐标的 Lap lace变换与空间坐标的 Fourier变换来求解热弹耦合方程,求解完成之后要将变换解进行反变换回到时间-空间坐标中,求解过程比较复杂且较难获得解析解.

有限元法凭借其能够有效地处理热弹耦合问题及复杂的模型结构,并且能够得到模型全场的数值解,进而在脉冲激光激发超声的理论研究中发挥了重要的作用[9-13].本文采用平面应变有限元法,考虑了热弹耦合过程中材料热物理参数虽温度的变化,在两维平面内模拟了激光线源辐照材料表面激发声表面波的物理过程,以及声表面波与规则表面微缺陷之间的相互作用过程.数值模拟结果建立了激光源作用位置以及表面微缺陷深度与声表面波时域位移信号特征之间的联系,为基于时域信号波形特征定量反演表面微缺陷深度提供了理论依据.

1 热弹耦合理论

激光脉冲线源辐照铝板表面的三维模型如图1所示,选取线光源的长度方向作为三维直角坐标系中Z轴方向.同时保证表面缺陷的走向与线光源平行,而且表面缺陷的尺寸沿 Z向保持不变.铝板具有足够的厚度以保证其远大于表面波波长,进而可将其视为均匀的、各向同性的线弹性半空间模型.弹性波在铝板中的激发和传播过程都可以采用与 Z方向坐标无关的场函数来近似表示,图1描述的三维热弹性动力学问题就可以简化为图2表示的两维平面问题进行处理.由于脉冲激光作用于铝板表面,在铝板近表面区域产生的瞬态温升一般维持在 ns量级,进而材料机械变形对温度场的影响可以忽略[5],热弹双向耦合的微分方程可以简化为顺序耦合的控制方程.

在图2给出的 X-Y平面内,热弹耦合的控制方程可以简化为[5]

式中:T(x,y,t)代表模型内部的瞬态温度场分布;U(x,y,t)表示位移向量场;k代表热传导系数;U表示热弹耦合常数且可以表示为U=(3λ+2_)T T,T T用来表征线性热膨胀系数.

图2中模型上表面 A,B,C,D 4点分别表示激光脉冲线源的辐照中心,它们到表面缺陷左边沿的距离分别为 0.8mm,0.6 mm,0.4mm和 0.2 mm.

在热分析中,模型上表面激光辐照区域满足的边界条件可以写为

图1 线源激光辐照样品含缺陷样品示意图Fig.1 Schem atic diagram of the sample irradiated by the line focused laser

图2 两维平面模型示意图Fig.2 Schematic diag ram of the cross section of sample

其他各边均按绝热处理:这里 Q(x,t)表示脉冲激光经过 y=h边上的辐照区域而注入模型的能流,可根据激光脉冲能量的时空分布特征表示为[5]

式中:f(x)与 g(t)可分别表示为

式中:x0是激光线源中心的横坐标;E0是线源单位长度上激光输出的脉冲能量;A(T)代表样品表面对入射激光的吸收率;RG是高斯型激光线源的半宽;t0表示激光脉冲的上升时间.模型的其它边界均按绝热条件处理.

此外,温度场及位移场分析需满足的初始条件可写为[11]

2 有限元方法

热弹控制方程的有限元形式可以表示为[9-10]

利用有限元法进行热弹分析时,温度场与位移场分析分别属于不同场变量的分析,进而单元属性要依据分析过程而发生改变.在进行温度场分析时,节点自由度为节点温度值;而进行位移场分析时,节点自由度为节点上的位移矢量.尽管温度场和位移场之间存在着相互耦合的关系,然而在热弹条件下,位移场对温度场的影响很小,可以忽略[5].所以耦合分析通常采用顺序耦合的方式,首先将激光荷载视为热流输入边界进行热分析来计算模型中的瞬态温度场,然后在结构分析中将瞬态温度场作为体载荷来计算瞬态位移场.

3 数值结果与讨论

3.1 模型及材料参数

采用边长为 20μm 4节点的平面矩形单元对求解区域进行网格划分,整体有限元模型的长与宽分别取为 16 mm,10mm.在模型中采用规则的矩形凹痕 (slot)来代替实际材料中的表面缺陷,将凹痕的宽度取为 60μm以趋近现实中的表面缺陷.激光照射到铝板上表面,铝板吸收激光能量导致模型内部局部区域温度迅速升高.设吸收的激光能量全部转化为热能,激光脉冲的上升时间为 10 ns,线源光斑的半宽取 100μm,单脉冲激光能量为 3.5 m J.铝材料的热物理参数详见表1.

表1 计算中所采用的热物理参数Tab.1 Thermo-physical parameters of alum inum used in the calculation

3.2 不同激发点产生的表面波位移信号

图2所示的模型当中表面缺陷的深度为 200μm,当激光分别作用于模型上表面 A,B,C,D 4点,在距离缺陷左顶点 2.6 mm的接收点 R得到的时域位移信号曲线如图3(a)～ 3(d)所示.图3(a)中曲线表示出了激光辐照铝板表面激发的声表面波模式,其中首先出现的是沿 x轴负向传播直接到达节点 R的掠面纵波 (sP)与 Ray leigh波模式(R),它们的传播速度分别为 6 310m/s与 2 920m/s;接下来出现的 PR模式是由沿 x轴正向传播的掠面纵波到达表面缺陷左边沿后模式转化变为 Rayleigh波并沿 x轴负向以 2 920m/s的速度传播到达接收点 R,这一结论我们在文献 [11]中已给出证明,这里不再赘述.

图3 激光光源分别作用于图2所示的模型上表面 A,B,C,D 4点时节点 R得到的时域位移信号Fig.3 Tempo ral displacem ent signal of node R as the laser source impinging on the positions denoted by A,B,C,D in Fig.2

图3(a)中标出的 RR模式是由光源激发的 Rayleigh波模式中沿 x轴正向传播的部分到达表面缺陷左边沿后反射回到接收点 R的位移信号;紧随反射 Rayleigh波位移信号之后出现了明显的位移振荡信号(图 3(a)中已用虚线方框标出).图3(b)～ 3(d)分别给出了激光光源分别距离表面缺陷左边沿0.6 mm,0.4mm,0.2mm时的位移信号,由图可知,随着激光源向表面缺陷不断靠近,Ray leigh模式(R)与 PR模式、RR模式的位移信号的时间间隔逐步缩小,同时由这三种模式重叠而产生的正向位移信号逐步增大,最后形成了一个典型的双极性 Rayleigh波 (bR)位移信号,bR位移信号的峰-峰值与单极瑞利波 (R)相比增加了 2.5倍左右,这样显著的强度变化非常有利于探测表面微缺陷的存在和走向.

3.3 表面缺陷深度对声表面波时域位移信号的影响

在图2所示的模型中,激光线源中心位于 D点,同时将距离缺陷左顶点 2.0mm的位置作为位移信号采集点 R.表面缺陷的深度分别取 0μm(即表面无缺陷的情形 )、40μm,80μm和 120μm时,接收点R得到的表面位移-时间响应曲线如图4所示:其中的实线代表了无表面缺陷存在时接收点 R得到的表面位移信号;其余三条虚线分别表示缺陷深度分别取为 40μm,80m,120μm时,在 R点得到的表面位移响应曲线.当模型表面无缺陷存在时,激光产生的掠面纵波及 Rayleigh波的位移信号都具有显著的单极性特征;当表面缺陷深度不为零时,掠面纵波与 Ray leigh波位移信号都转变为双极性,而且随着表面缺陷深度的增加,掠面纵波与 Rayleigh波位移信号的双极性特征更加明显.在激光激发的声表面波各模式中,双极性瑞利波具有显著的强度而在实验中易于观测,进而可以成为判定表面微缺陷存在的主要依据.

图4 激光激发的声表面波时域信号随表面微缺陷深度的变化规律Fig.4 Laser generated su rface acosutic waves on the samplewith varied depths

图5 双极性 Rayleigh波峰-峰值随表面微投缺陷深度的变化规律Fig.5 Peak-to-peak values of bipolar Rayleigh pulse versus stot depths

图5给出了表面缺陷深度从 0μm～ 200μm之间变化时双极性 Rayleigh波 (bR)峰-峰值的变化曲线.当表面缺陷深度在 0μm～ 60μm范围内增加时,bR波位移信号的峰-峰值迅速增长;而当深度在80μm～ 140μm范围内增加时,峰-峰值的增长显著放缓;而从当深度在 140μm～ 200μm之间变化时,峰-峰值基本保持不变.这一趋势表明 Rayleigh波位移信号峰-峰值随表面缺陷深度的变化规律较为复杂,进而利用 bR波位移信号强度的显著变化可以有效地判定表面缺陷的存在,却很难凭借峰-峰值的变化达到定量检测表面缺陷深度的目的.

图6表示出了紧随 bR波位移信号之后出现的振荡位移信号,同时比较了振荡位移信号的时域特征随表面缺陷深度的变化规律.在图6所示的时域振荡曲线上选取两次正向位移极大值点对应的时间间隔(用W T表示)作为一种振荡持续时间的指标.图7给出了W T这一指标随表面缺陷深度的定量变化关系,图7中实点表示每一缺陷深度计算所得的持续时间值,而实线表示线性拟合后的变化曲线.图7中实线直观地表明振荡时间间隔W T与表面缺陷深度之间存在着近似线性的变化关系,而这种线性关系为实现表面缺陷深度的定量检测提供了重要的理论依据.为了证明这种线性关系的普遍性,在数值模拟中分别采用两种不同半宽的线光源作用于同一模型表面,来分析光源参数对振荡位移信号的影响.

图6 振荡位移信号随缺陷深度的变化规律Fig.6 Laser generated oscillation signals versus slot depths

图7 振荡位移信号的时间间隔 (δT)随缺陷深度的变化规律Fig.7 Temproal intervals of oscillation signals versus slot depths

3.4 线光源宽度对声表面波位移信号的影响

单脉冲能量为 3.5m J的激光线源,半宽分别取为 50μm与 100μm,在模型表面无缺陷存在的情况下得到的位移信号曲线如图8(a)所示:图中首先出现的正向位移信号峰 sP,代表了掠面纵波的到达,随后的单极性负向位移信号脉冲 R表示 Rayleigh波模式;图8中虚曲线表明半宽为 50μm的激光线源激发出的声表面波位移信号具有更加显著的振幅.

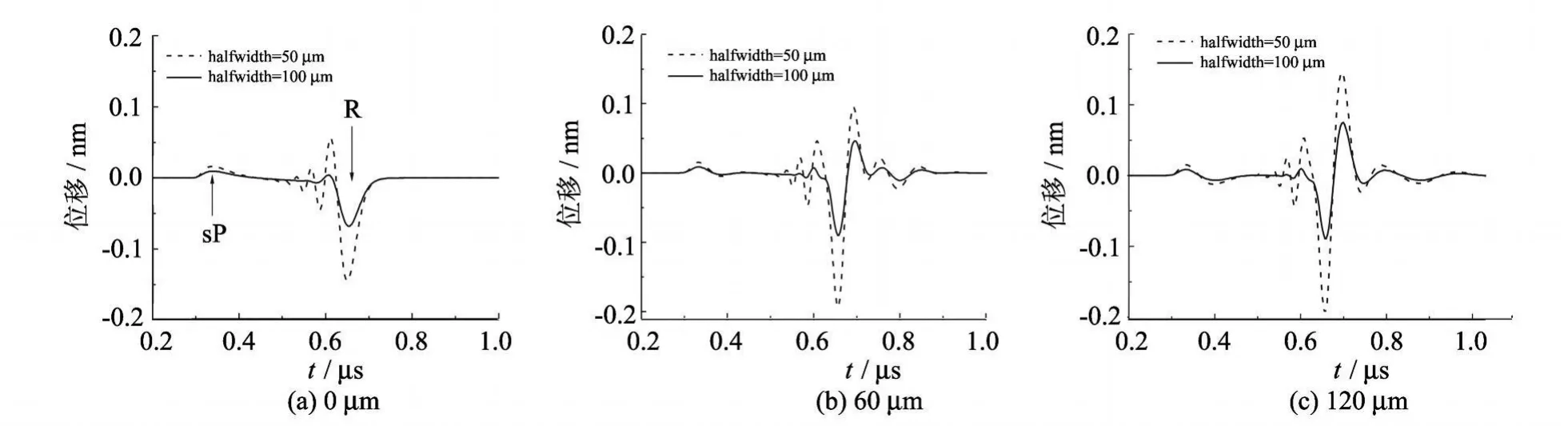
图8 不同半宽(50μm与 100μm)的激光线源辐照铝板表面产生的声表面波Fig.8 Tem poral displacemen t signals generated by laser line source w ith 50μm and 100μm half-wid th impinging on the sam ple with slot of 0μm depth

当表面缺陷的深度取为 60μm,分别采用半宽为 50μm与 100μm的激光线源辐照样品表面,并保证激光线源的中心位于模型上表面 D点.在接收点 R得到的位移信号曲线如图8(b)所示;图8(c)给出了表面缺陷深度为 120μm时,采用半宽为 50μm与 100μm的两种线光源辐照样品表面产生的位移信号曲线.图8(b)与 8(c)中的曲线表明:不同的线源半宽会显著改变振荡位移信号的强度.半宽为50μm的线光源产生的振荡信号强度明显大于半宽为 100μm的情形.而当两种宽度的线光源辐照深度为 60μm与 120μm的表面缺陷模型时产生的振荡信号持续时间W T值见表2.表2数据显示:当表面缺陷深度取定时,不同半宽的线光源激发出的声表面波中振荡信号的W T在误差范围内是相等的,即表面缺陷的深度与W T存在着一一映射的关系;不同半宽的激光线源只会影响振荡信号的相对强度,而不改变其W T.

由此可推断位移响应曲线中的振荡信号来源于激光激发的 Ray leigh波中某一波长成分(或者说有限的波长范围)在表面缺陷边沿上形成的振荡.当表面缺陷深度较大时,Rayleigh波模式中波长较长的低频成分在缺陷边沿形成振荡,从而产生的振荡位移信号具有较长的 W T;而当表面缺陷深度较小时,Rayleigh波模式中波长较短的高频成分在缺陷边沿形成振荡,进而产生的振荡位移信号具有较短的W T.因此,表面缺陷对线光源激发的 Rayleigh波发挥了一种选频滤波的作用.尽管脉冲激光激发出的 Rayleigh波模式波长成分比较丰富,但其中只有一种波长成分(或者说有限的波长范围)可以在某一深度的表面缺陷边沿上形成振荡,进而对应唯一的持续时间 (W T).综上所述,利用激光激发的声表面波中振荡位移信号的持续时间可以实现定量检测表面缺陷深度的目的.

表2 振荡信号时间间隔Tab.2 The temp roal intervals(W T)of oscillation signals

4 结 论

本文采用有限元法研究了脉冲激光线源在含有表面缺陷的铝板模型中激发声表面波的物理过程,分析了激光源作用位置的改变对声表面波时域波形的影响.研究发现当激光源逐渐靠近表面缺陷时,同测的接收点得到的位移信号波形将呈现由单极性向显著的双极性过渡;双极性 Rayleigh波信号强度的显著增强的趋势将有利于检测表面微缺陷的存在.紧随双极性 Rayleigh波之后出现的振荡位移信号,其持续时间将随着表面缺陷深度的增加而呈现出线性的递增趋势;利用这一趋势为定量检测表面缺陷深度提供理论依据.另外,光源半宽的改变仅仅导致振荡信号的相对强度发生改变,而对振荡信号的持续时间并无影响.由此可见,表面缺陷的深度唯一地决定了激光激发的声表面波中能够形成振荡的波长成分.进而利用表面缺陷对声表面波的这一滤波效应可以定量地测量表面缺陷的深度.

[1] Dewhurst R J,M cKie A D,Palmer SB.Further evidence for two-component surface acoustic w ave reflections from surface breaking slots[J].Appl.Phys.Lett.,1986,49(25):1694-1695.

[2] Cooper J A,Crosbie R A,Dew hurst R J,et al.Surface acoustic w ave interac tions with c racks and slots:a noncontacting study using lasers[J].IEEE Trans.U FFC,1986,UFFC-33:462-470.

[3] Shan Q,Dew hurst R J.Surface-breaking fatigue crack detec tion using laser ultrasound[J].Appl.Phys.Lett.,1993,62(21):2649-2651.

[4] K romine A K,Fom itchov P A,Krishnasw amy S,et al.Laser u ltrasonic detection of surface-breaking discontinuities:scanning laser source technique[J].Mater.Eval.,2000,58(2):173-177.

[5] Achenbach JD.Laser excitation of surface w avemotion[J].Journal of the Mechanics and Physics o f Solids,2003,51:1885-1902.

[6] Sohn Y,Krishnasw am y S.Mass sp ring latticemodeling o f the scanning laser source technique[J].U ltrasonics,2002,39:543-551.

[7] Sohn Y,K rishnaswamy S.Interaction of a scanning laser-generated ultrasonic line source with a surface-breaking flaw[J].J.Acoust.Soc.Am.,2004,115(1):172-181.

[8] A rias I,Achenbach JD.A model for the ultrasonic detection o f surface-breaking cracks by the scanning laser source technique[J].Wave Motion,2004,39:61-75.

[9] Xu Baiqiang,Shen Zhonghua,Ni Xiaowu,et al.Numerical simu lation of laser-induced u ltrasonic by finite element m ethod[J].Journal of Applied Physics,2004,94(4):2116-2122.

[10] Xu Baiqiang,Shen Zhonghua,N i Xiaowu,et al.Finite elementmodeling of laser generated u ltrasound in coatingsubstrate system[J].Journa l o f App lied Physics,2004,94(4):2106-2115.

[11] Guan Jianfei,Shen Zhonghua,NiXiaowu,et al.Numerical simulation of the reflected acousticw ave components in the near field o f sur face defects[J].J.Phys.D: App l.Phys.,2006,39:1237-1243.

[12] Jian X,Fan Y,Edwards R S,et al.Surface-breaking c rack gauging with the use of laser-generated Ray leigh waves[J].J.Appl.Phys.,2006,100(6):064907-1-064907-6.

[13] 关建飞,沈中华,倪哓武,等.激光声表面波检测铝板表面凹痕的数值研究 [J].测试技术学报,2006,20(8):390-396.

Guan Jian fei,Shen Zhonghua,Ni Xiaowu et al.Numerical analysis of the surface notch inspection by laser generated Ray leigh waves on Aluminum p late[J].Journal of Test and Measurement Techno logy,2006,20(5):390-396.(in Chinese)