测试性建模与分析中的故障概率获取方法研究❋

王成刚,王学伟,周晓东

(1.海军航空工程学院基础实验部,山东烟台 264001;2.海军航空工程学院控制工程系,山东烟台 264001）

0 引 言

在现场测试中,有些子系统或较大模块包含有多个部件,为了系统安全和减少测试时间,经常采用备份模块替换可疑故障模块的办法,而不是修复具体部件.所以故障源不用定位到具体部件,而只需隔离到模块就足够了[1].另外,实际测试中还经常采用元件替换的方法进行故障定位.替换可疑元件与修复不同,它不进行精确诊断而把潜在故障源 /模块替换掉,即该元件状态不能确定是故障,也用正常的元件替换它并重新测试.

对于模块化诊断和模糊组替换诊断这些含实用特性的诊断方法,传统的故障概率计算方法将模块或模糊组内元件的概率累加得到,而实际上存在一些内在问题而使利用这种方法得到的结果产生很大误差.假设某模块有两个元件 A和 B,其中元件 A的故障率是另一元件 B的几十倍.因为每次 A发生故障时该模块被替换,B从未发生故障.尽管元件 B故障的可能性存在,但其发生故障的相对可能性大大的减小了.总的来说,多元件模块的故障率并不一定想预计的那样高.当各元件的故障率差别较大时,比起各元件具有相同故障率时的模块的故障频率实际上还是减小了.

这种情况在同一模糊组中的不同元件的功能中同样存在.例如 C和 D同为某故障模糊组中的元件,其故障率差别很明显,比方说,C的故障率比 D大几十倍.由于它们可达性都很差,所以维修中经常被一起替换掉.因为每次随元件 C的故障一起被替换,所以元件 D的故障被大大的延迟了.而传统的故障概率计算方法仍然为二者故障概率之和.

基于以上分析,不难看出,对于采用含实用特性诊断方法的系统而言,传统的故障概率计算方法[2-3]已经不适用于其测试性建模和分析,因此本文提出利用蒙特卡罗仿真获取故障概率.

1 传统故障概率计算方法及其不足

1.1 传统故障概率计算方法

在测试性建模、分析与评估和诊断策略的设计中,需要计算系统中每个故障模式的概率.基于单故障、系统确定故障状态的假设,首先探讨给定故障概率分布下的先验概率计算方法,然后利用该概率得到条件故障概率[1].

1.1.1 故障先验概率

元件故障时间的累积密度函数为 Fi(t).t=0时刻元件开始工作;t=ti时刻该元件无故障,而在 t=t2时刻发现故障,也即在 (t1,t2]时间段内发生的故障.所以元件 ci的故障先验概率为

所以,有了元件的故障时间累积分布函数就可以计算其故障的先验概率.

1.1.2 条件故障概率

对于维护良好的系统而言,假设绝大多数情况下只有单故障发生.对于许多任务系统,由于测试频繁且经常性的恢复,这种假设是很有效的.S={s0,s1,s2,… ,sm}是系统故障状态集;P′={p′1,p′2,… ,p′m}为各元件故障的先验概率.假设各故障状态 si,1≤i≤m是独立的.

假设 SI⊆S表示故障状态集,其中所有的故障状态 si∈ SI都发生了,而所有的 sj∉ SI均未发生.基于系统状态独立的假设,上述事件的概率为

因此,系统无故障的概率为

如果假定在指定时间系统单故障或无故障情况下,只有 SI={sj}∀si∈S和 SI=∅这些事件能发生[4].所以各系统状态的单故障概率(s0为无故障状态)为[1,4,5]

1.1.3 含实用特性诊断的故障概率计算

1)模块化诊断

模块化诊断与故障状态级诊断的整体策略是一致的.定义组成系统 (m+1)个状态的模块有限集为M={M0,M1,… ,ML},其中 M0表示系统无故障状态.通过映射K:s→M,描述系统状态与模块集之间的关系,其中 K(s0)=M 0,K(si)=Mk,1≤i≤m,1≤k≤l,si为对应系统模块的故障状态.

为了解决模块化诊断问题,序贯测试算法如下:

①在故障状态级序贯测试算法中,终端节点定义为只包含集 S中单个故障状态的节点,而对应含实用特性诊断,终端节点定义为包含单个或多个故障状态的单个模块.

②对模块化诊断,启发函数计算采用可疑集节点 x的模块累积概率分布.为了描述这个差别,考虑包含故障状态集可疑集节点 x,设

2)替换诊断

替换诊断和模块化诊断的序贯测试算法类似,其终端节点定义为故障模糊组或模块.启发函数计算采用可疑集节点x的故障模糊组或模块累积概率分布.

1.2 传统故障概率计算方法的不足

当用上述传统方法统计故障率时,存在一些内在问题而使利用这些值预计实际诊断能力时产生很大误差[6].

1)传统的计算方法不考虑历史维修数据,即只考虑全部可能故障组,而不考虑故障的顺序.但是,这种计算方法是基于一种无效的假设,即随着时间推移,每个故障是按它们各自的故障概率失效的.相反,大多数复杂系统包含许多元件,而这些元件并不是按可靠性数据所估计的那样发生故障.究其原因,不在于这些功能的可靠性,而是其它元件的相对不可靠性.

2)传统的故障分辨率计算方法只能预测很长时间内的诊断性能.因为故障分辨率通常只有运行了足够的时间,才能正确反映系统的诊断行为.在实现之前,故障必须出现许多次.因为许多系统元件是高可靠的,这也就意味着必须运行相当长的时间才能接近传统故障分辨率计算方法所能预计的诊断性能.

3)传统的故障分辨率计算方法不能区分隔离到同一故障组的不同故障组合.对于单故障假设的诊断策略或仅依赖模块替换进行维护的系统而言不存在该问题,但若系统采用多故障诊断策略,当同一故障组是由故障元件的不同组合得到时,顺次更换部件可能导致不同的诊断行为.

2 基于蒙特卡罗仿真的故障概率获取

蒙特卡罗方法又称统计模拟实验法,它以统计抽样理论为基础,利用随机数通过对有关的随机变量的统计、抽样实验或随机模拟,以求得统计特性量(如均值、概率等)作为待解问题的数值解,是求解工程技术问题近似解的一种数值计算方法[7,8].

2.1 模型和假设

对于含实用特性诊断方法,为获取其故障概率,进行蒙特卡罗仿真需做如下假设:

1)系统模块或者工作,或者失效,系统也是如此;

2)模块或模糊组中每个部件的寿命分布已知;

3)模块或模糊组中每个部件发生故障是相互独立的;

4)采用模块化诊断时,故障的模块在系统发生故障进行维修时,由一个新模块代替;

5)采用替换诊断时,发生故障的模糊组在进行维修时,替换模糊组中的所有元件;

6)每个元件的更换时间忽略不计,更换或修理对系统没有影响.

2.2 元件的抽样

对于元件的寿命分布函数为连续函数,且其反函数存在的情况,可采用直接抽样法.设随机变量a具有分布函数 F(x),其一般形式为

式中:f(t)为分布密度函数,根据直接抽样的基本定理,则

是 [0,1]上均匀分布的随机变量.Z产生的简单子样 Z1,Z2,…,Zn即为随机数序列.

若分布函数 F(x)的反函数存在,且 F(x)为单调递减连续函数,则有连续型分布的直接抽样方法为

式中:a是以 F(x)为分布函数的随机变量.因此,可用随机数来产生随机变量a的抽样值.对于无法给出反函数或反函数求解困难的连续分布函数,可采用间接抽样法得到.

2.3 基于蒙特卡罗仿真的故障概率获取

当利用蒙特卡罗诊断仿真生成的数据进行故障概率计算时,不会产生传统计算方法内在的偏差.

1)在计算故障率时会自动考虑每个单元的更换历史.当一个元件被更换后,无论它是确实有故障,由于模糊组被错误的更换了,或者是故障预计决策的原因提前更换了,其下一个故障都是从该时刻算起.换言之,每个仿真功能故障考虑了各元件的维修历史.

2)因为诊断仿真可以在任意期望的时间内执行,统计结果不必在工作很长时间后完成.相反,短时间内的仿真可以产生期望很长时间内才能得到的故障.因为仿真故障的发生不仅依据元件的 M TBF,而且还与寿命分布曲线有关,保留了一定的随机性.为了减小这种随机性,最终的度量采用了大量的仿真进行平均.

3)根据元件的寿命分布,按照上述模型和假设及仿真规则,统计仿真寿命期间的故障次数和更换次数,最后进行平均即可得到含实用诊断特性诊断中的故障率等参数.

3 实例仿真

选取文献 [6]中例 1,以模块化诊断为例进行算法验证.该模块由 4个可更换单元组成 (A,B,C和D),如图1所示,其中具有 5个功能(单元 A,B和 C各关联一个功能,单元 D关联两个功能).各单元寿命均服从标准正态分布.为简化仿真分析过程,假设各单元故障率均为 1 000 h-6.

不难看出,该模块可将故障隔离到两个模糊组 {A,D}和 {B,C,D},由传统的故障率计算方法得到故障率如表1所示.

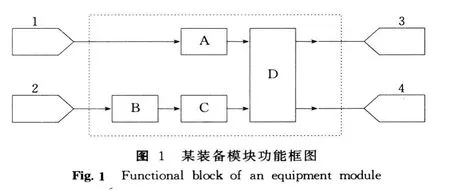
表1 基于传统计算方法的故障率Tab.1 Fault probability obtained by traditionalmethod

由表1数据可以看出,在各单元等故障的假设下,故障频数与单元的数量是成正比的,这种计算方法看似是很准确的.

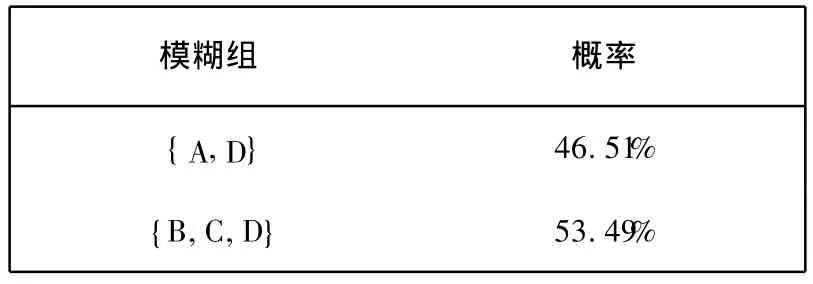
表2 基于蒙特卡罗仿真的故障率Tab.2 Fault probability obtained by monte carlo simulation

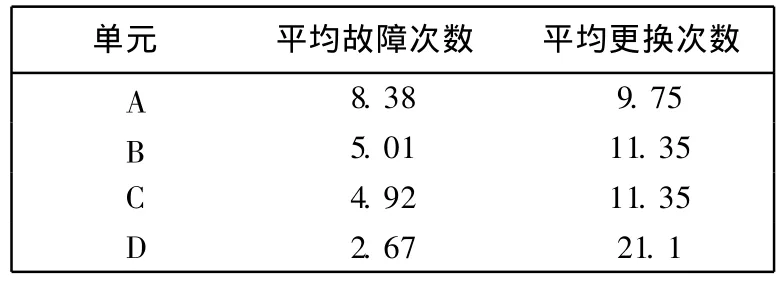
表3 仿真中各单元的平均故障及更换次数Tab.3 Average simulated failure and replacement tim es of each item

利用基于蒙特卡罗仿真的故障概率获取方法,模块运行时间 10 000 h,仿真 1 000次,每次故障发生后立即进行模糊组更换,更换时间忽略不计,Matlab仿真流程如图2所示,仿真结果见表2.

由表2看出,利用基于蒙特卡罗仿真的故障概率修正算法得到模糊组 {A,D}的故障率比传统计算方法高了 9%.表3给出了利用仿真得到的各单元的平均故障次数和更换次数.

虽然 4个单元的寿命服从同参数的标准正态分布,但仿真中各单元故障次数并不相同.这并非源自仿真的不准确,而是由每次故障诊断时模糊组更换导致无故障单元被提前更换造成的.如果没有采用模块化诊断或替换诊断,那么每个单元在仿真中的故障次数大约均为 10次.由于提前更换,所以每个单元的故障比通过寿命分布曲线计算的故障率低(因为每次都是在发生故障前被更换,所以下次发生故障的时间延迟了).由本例可知,单元 A被提前更换的原因是测试 3发现故障,单元 D故障次数多的原因是:测试点 3和 4故障率近似相等,但低于单元 A,因为导致 A提前更换的故障少于 B和C.

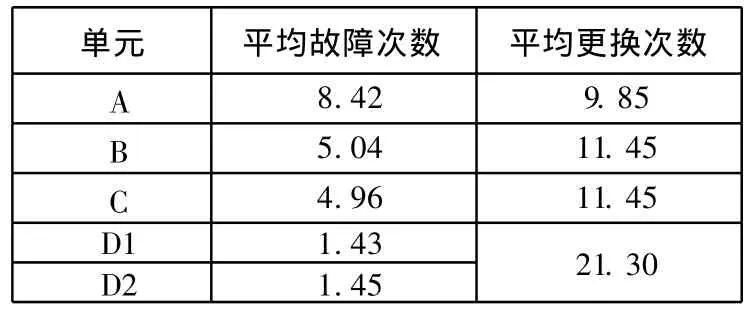
表4 文献 [6]仿真中各单元的平均故障及更换次数Tab.4 Average simulated failure and replacemen t times of each item in literatu re[6]

表4为文献 [6]中仿真得到的各单元的平均故障及更换次数.

对比表3和表4可以看出,对于模块化诊断而言,二者的仿真结果几乎相等,这也表明本文提出的含实用特性诊断中的故障概率获取方法是有效的.作为测试性建模、分析与评估的内容之一,该方法也可用于模型修正[9].

4 结 论

对于采用含实用特性诊断方法的系统而言,传统的故障概率计算方法不再适用,本文提出了基于蒙特卡罗仿真的故障概率获取方法.仿真分析表明,对于采用含实用特性诊断方法的系统而言,基于蒙特卡罗仿真的故障概率获取方法得到的故障率更加真实可靠,能为测试性建模、分析与评估和序贯测试诊断策略的设计提供更加准确的依据.

[1] Vijaya R,Shakeri M,Pattipati K.Op timal and near-op timal test sequencing a lgorithms with realistic testmodels[J].IEEE Transactions on Systems,Man,and Cybernetics,Part A,1999,29(1):11-26.

[2] M IL-STD-2165 Testability Program for Electronic Systems and Equipments[S].Department o f Defense,W asgington,1985.

[3] M IL-STD-2165A Testability Program for Systems and Equipments[S].Department of Defense,Wasgington,1993.

[4] Shakeri M,Pattipati K R,Raghavan V,et al.Near-Optimal Sequential Testing Algorithm s for Mu ltip le Fau lt Iso lation[C].IEEE Internutional Con ference on Systems,Man and Cybernetics,1994:1908-1914.

[5] Shakeri M,Raghavan V,Pattipati K R.Sequentia l testing algorithms formu ltip le fault diagnosis[J].IEEE Trans.on SMC,2000,30(1):1-14.

[6] Gould E,Hartop D.Simulation-based techniques for calculating fault resolution and false removal statistics[C].IEEE Autotestcon,2000:465-480.

[7] Liu JS.Monte carlo strategies in scientific computing[M].Beijing:W orld Books Pub lishing Corporation,2005.

[8] 陈红霞,郭进,杨扬.可维修系统的故障率分析 [J].微机发展,2005,15(2):56-58.

Chen Hongxia,Guo Jin,Yang Yan.Failure rate analysis of repairab le system[J].Mic rocomputer Development,2005,15(2):56-58.(in Chinese)

[9] 王成刚,周晓东,杨智勇.多信号模型故障模式与信号概率关联算法研究 [J].测试技术学报.2009,23(4):362-365.

W ang Chenggang,Zhou Xiaodong,Yang Zhiyong.Study on correlation algorithm of failure rates for signals and failure modes in mu ltisignalmodel[J].Journal of Test and Measurement Technology,2009,23(4):362-365.(in Chinese)