一种建立复杂系统相关性矩阵的新方法❋
2010-02-09王子玲许爱强牛双诚陈育良
王子玲,许爱强,牛双诚,陈育良
(海军航空工程学院,山东 烟台 264001)
随着以电子信息技术为核心的现代科学技术迅猛发展及其在军事领域的广泛应用,装备系统的复杂性也越来越高.对于复杂装备系统,其组成单元之间的物理连接关系难以用模型准确表示,因此给装备系统的测试和诊断带来了极大的挑战.相关性模型不直接针对系统硬件设计进行描述,仅考虑系统测试和诊断过程中的测试部件之间的因果连接关系,并采用有向图的形式描述这些关系,这使得相关性模型不仅描述直观,而且建模难度低,成为复杂装备系统测试性设计分析和故障诊断中应用最多的一种模型.目前比较成熟且应用较多的相关性模型有信息流模型[1]、多信号模型[2,3]以及混合诊断模型[4]等.
基于相关性模型的故障诊断分为三步:首先建立被诊断系统的相关性模型;然后由相关性模型建立相关性矩阵;最后依据相关性矩阵进行测试性预计和故障诊断.目前国内外学者(包括工程界)的研究多集中于基于相关性模型的建模方法[1-4]以及基于相关性矩阵的测试性预计和故障诊断研究[5-12],针对如何由相关性模型得到相关性矩阵尚缺乏清晰系统的研究,然而这是基于相关性模型进行故障诊断的关键一步.本文在详细分析系统故障与测试之间相关性的基础上,提出了一种可用于建立复杂装备系统相关性矩阵的新方法.
1 问题描述
1.1 故障-测试相关性矩阵
故障-测试相关性矩阵(简称相关性矩阵),是被测对象的组成单元故障与测试相关性的数学表示形式,是对产品进行测试性分析和预计以及构造故障字典和诊断策略实施故障诊断的基础,一般定义为[13]

式中:第 i行矩阵为
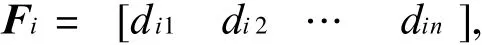
表示第 i个组成单元(或部件)故障在各测试点上的反应信息.它表明了 F i与各个测试点 Tj(j=1,2,…,n)的相关性.而第 j列矩阵
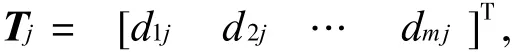
表示第 j个测试点可测得各组成部件的故障信息.它表明了 Tj与各部件 F i(i=1,2,… ,m)的相关性,其中

测试 T3和部件 F1的相关性,如果测试 T3能够观察到部件 F1的故障,则 d13=1,即测试 T3和部件 F1相关;否则 d13=0,即测试 T3和部件 F1不相关.
1.2 已有研究成果及本文的研究思路
文献 [13]给出了两种生成简单模型系统相关性矩阵的方法:测试性框图直接分析法和一阶相关性求解法,测试性框图直接分析法只适用于初选测试点不多的小型模型图;一阶相关性求解法亦无法对具有 AND节点(冗余系统)的复杂模型图求解相关性矩阵.Shakeri研究了冗余系统最小故障及其故障特征的建立方法[14],但是论文中没有对本文定义的第二类单故障作明确处理,也没有考虑具有开关节点(多模式系统)的复杂模型图相关性矩阵的计算与合并问题;Tu Fang研究了大型有向图的可达性算法[15],并提出了一种求解模型图中指定大小最小割集的方法,即首先建立元素数为 2的最小割集,然后建立元素数为 3的最小割集,……,这种方法迭代繁琐、计算复杂,而且也没有涉及到多种模式相关性矩阵的计算与合并问题.
为了研究方便,本文首先将被诊断系统的模型图分为三类:普通有向图;有 AND节点的有向图;有开关节点的有向图.普通有向图相关性矩阵的生成方法分为两步:可达性分析和相关性分析[14],此处不再赘述.本文主要研究有 AND节点的有向图相关性矩阵的生成算法和有开关节点的有向图相关性矩阵的建立方法,提出了一种计算复杂有向图模型相关性矩阵的新思路,最后应用案例系统进行了验证.
1.3 相关定义
定义 1 超集
存在集合 A和 B,如果集合 A是集合 B的真子集,那么集合 B就是集合 A的超集.
举例 Q1={a,d,e},Q2={a,b,c,e},则 Q2是 Q1的超集.
定义 2 最小集
集合 Q={Q1,…,Qk}的最小集 (minimal(or irreducible)set,或者称不可约集)为删除 Q中的所有超集 (super set)后的集合,即
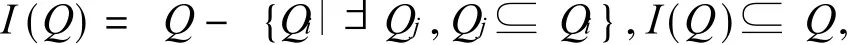
举例 Q1={q,d,e},Q2={b,c,e},Q3={a,b,c,e},I(Q)={Q1,Q2},因为 Q3是超集.
定义 3 碰集
集合 Q={Q1,… ,Qk}的碰集 (hitting set)为 H(Q)={H1,… ,Hq},其中

根据定义 2和定义 3,集合 Q的最小碰集就是 H(Q)的最小集,换句话说,删除所有超集以后的碰集即为最小碰集.
举例 假设集合 Q1={a,d,e},Q2={b,c,e},I(H(Q))={H1,…,H5},其中 H1={a,b},H2={a,c},H3={b,d},H4={c,d},H5={e},每一个 Hj和 Qk中至少有一个公共元素.
2 冗余系统的相关性矩阵的生成算法
冗余系统的有向图模型中必然有 AND节点,说 AND节点 ak具有 uk-out-o f-wk逻辑,指的是AND节点 ak共有 wk个输入,至少有 uk个输入为故障时,该 AND节点输出故障.按照这个逻辑,可以将冗余系统的故障分为两类:单故障和最小故障.单故障又分为两类,第一类是那些与所有 AND节点之间都没有任何通路的单个故障状态,第二类是指故障与某 AND节点之间有通路,但是该故障能够到达该 AND的至少 uk个输入,即该故障能够单独导致该 AND节点的输出故障.最小故障指的是最少数量的故障,它是一个集合,集合中的故障同时发生时的故障信号与各故障单独发生时的故障信号的合并不一样,即最小故障的关联测试集不等于最小故障中各单故障关联测试集的并集.建立冗余系统的相关性矩阵,需要分为以下几步:
1)建立第一类单故障-测试相关性矩阵 S1ST.
2)建立第二类单故障-测试相关性矩阵 S2ST.
3)将 S1ST和 S2ST合并为 SST,即系统单故障-测试相关性矩阵.
4)建立最小故障-测试相关性矩阵 MST.
5)将 SST和 MST合并,即为冗余系统的相关性矩阵.
2.1 建立 S1ST
根据第一类单故障的定义,定义第一类单故障-测试相关性矩阵为 S1ST={s1 tij},如果测试 tj能够检测故障 si,并且在故障 si和测试 tj之间不存在任何 AND节点,则 s1 tij=1;否则 s1 tij=0.因此如果没有AND节点,则 S1ST=D.建立 S1ST的过程分为两步:首先应用 Reachability_Analysis[14]获得可达性;然后用图1所示的算法得到相关性.图1中用方框标出来的语句,即是对故障节点和测试节点之间的AND节点处理方法.


图1 第一类单故障-测试相关性分析算法Fig.1 Dependency analysis algorithm betw een the single fault and test
2.2 建立 S2ST
首先寻找 AND节点 ak的第二类单故障需要如下两步:
1)搜索能够直接到达某一 AND节点 ak第 l个输入的所有故障状态,用集合 SA(ak(l))(1≤l≤wk)表示.所谓直接到达,指的是在 SA(ak(l)(1≤l≤wk)中的故障状态与 AND节点 ak之间没有 AND节点.
2)对 SA(ak(l))(1≤l≤wk)中的所有故障状态,判断其是否同时在不少于 uk个 SA(ak(l))(1≤l≤wk)中存在,若是,则该故障状态为第二类单故障.
根据第二类单故障的定义,这一类故障也就是能够单独导致某一 AND节点输出故障的单故障状态,这些单故障与测试之间的相关性,与对应 AND节点与测试之间的相关性是相一致的.为此,首先定义 AND节点-测试相关性矩阵 AT={atkj},表示 AND节点和测试之间的相关性,如果测试 tj能够检测到 AND节点 ak,并且在测试 tj和 AND节点 ak之间没有其它 AND节点,则 atkj=1,否则 atkj=0.定义第二类单故障-测试相关性矩阵 S2ST={s2tij},表示如果故障能够到达 AND节点 ak的 uk个输入,且 atkj=1,则 s2 tij=1,否则 s2 tij=0.即如果 si是 AND节点 ak的第二类单故障,则 s2 tij=atkj.
2.3 建立 SST
将 S1ST和 S2ST合并,得到系统单相关性矩阵 SST.合并原则为:①将 S2ST矩阵的各行加入到S1ST矩阵中;②将具有相同故障状态的各行向量相或,作为新的行向量,删除原来对应的行;③将具有相同行向量的故障 si合并为一行,删除多余的行.即得到 SST.
2.4 建立 MST
文献 [14]中给出了一种最小故障算法,这里给出另一种最小故障算法.具体步骤如下:
对 AND节点 ak
1)搜索能够直接到达 AND节点 ak第 l个输入的所有故障状态和 AND节点的组合,分别用集合SA(ak(1)),SA(ak(2)),… ,SA(ak(l)表示 .
2)寻找能够到达该 AND节点至少 uk个输入端的 AND节点,假设有 q个,将其储存在集合 Ak中,并且从 SA(ak(l))(1≤l≤wk)中去掉该 q个元素.
3)若 SA(ak(l))(1≤l≤wk)中存在 AND节点,则
3.1)对于 SA(ak(l))中的每一个 AND节点,比如 ar,执行步骤 1),2).若 SA(ar(1)),SA(ar(2)),… ,SA(ar(l))中没有 AND节点,则
a.去掉 SA(ar(1)),SA(ar(2)),… ,SA(ar(l))中的超集;
b.寻找该 AND节点的第二类单故障并将其从 SA(ar(1)),SA(ar(2)),…,SA(ar(l))去掉;
c.求 SA(ar(1)),SA(ar(2)),… ,SA(ar(l))的最小碰集,记作 H(ar);
d.对被存在 Ar中的 AND节点的处理方法与 ak一样,最后得到其 H′(r);
e.MS(ar)= H(ar)∨ H′(r);
f.将 SA(ar(1)),SA(ar(2)),… ,SA(ar(l))中的 AND节点 ar用 MS(ar)代替.
3.2)若 SA(ar(1)),SA(ar(2)),… ,SA(ar(l))中有 AND节点,则重复 3.1).
4)若 SA(ak(l))(1≤l≤wk)中不存在 AND节点,执行 a.~ f..
最终所有 AND节点的最小故障被存储在MS(◦ )中,因此MS(ak)中的所有元素都是能够到达 AND节点ak的uk个输入端的最小故障,即M S(ak)中的每个最小故障均能导致 AND节点ak的输出故障.
对 MS(ak)中的所有最小故障来说,能够观察到 AND节点 ak的所有测试都能够观察到 MS(ak)中的所有最小故障.所以 AND节点 ak与测试 tj之间的相关性是 MS(ak)中最小故障与测试之间相关性的一部分.另外最小故障中的每个单故障与测试的相关性也是最小故障与测试之间相关性的一部分.所以定义最小故障与测试之间的相关性矩阵 MST={mstn j},如果 MS(ak)中某一最小故障 m sn的任一单故障状态能够被测试 tj观察到,或者 atkj=1,则 mstn j=1,否则 mstnj=0.
2.5 矩阵合并
将上述 S1ST,S2ST和 MST三个矩阵合并,即将 SST和 MST合并就可以得到整个冗余系统的相关性矩阵,合并原则为:
1)将 MST矩阵的各行加入到 SST矩阵中;
2)将具有相同最小故障 msn的各行向量相或作为最小故障 msn新的行向量,删除原来的最小故障msn对应的行;
3)将具有相同行向量的最小故障 msn合并为一行,删除多余的行;
4)所得矩阵即为所求.
3 多模式系统相关性矩阵的建立方法
多模式系统的一个明显特征就是并非所有的测试在每一个模式中都是可行的,测试被分配在多个模式下,同时,同一个测试在不同的模式下具有不同的诊断能力或者(和)具有不同的测试费用.多模式系统的另一个明显特征就是其有向图模型中必然有开关节点,这就决定了多模式系统在每一种模式下都有一个相关性矩阵.为了叙述方便,这里假设多模式系统的可选模式集 M={m1,m2,…,mw},诊断之前的初始模式已知;对于每种模式 mi(1≤i≤w),存在一个有限的二元测试集 Ti={ti1,ti2,…,tini)和相关性矩阵 Di= [dijk],在模式 mi中,如果测试 tik能检测到故障状态 sj,则 dijk=1;否则 dijk=0.因为对系统进行故障诊断时是针对系统故障这一事实,而不是针对系统在某种工作模式下的故障,因此需要将几种模式下的相关性矩阵进行合并,合并后称为系统相关性矩阵.合并原则如下:
1)系统相关性矩阵的行元素集为每种模式 mi(1≤i≤w)下所有故障状态的并集,对于仅在某一或者某几种模式下出现的故障状态,其关联测试集不变,其余元素用 0填满;
2)系统相关性矩阵的列元素集按照如下方法确定:
2.1)考察相关性矩阵 D i= [dijk](1≤i≤w),将符合如下条件的测试列为公共测试:
a.该测试存在于每个 D i(1≤i≤w)中;
b.在每个 Di(1≤i≤w)中,该测试具有相同关联故障集;
c.在每种模式 mi(1≤i≤w)下,执行该测试的费用相同;
2.2)在公共测试后,依次排列每种模式下不符合公共测试条件的其它测试,并用模式索引将其分开.
4 案例分析
考虑某型军用飞机供电系统,其有向图模型如图2所示,其中开关 K1和 K2在任何时刻只有一个闭合,分别表示交流供电模式和直流供电模式.AND节点集为 A={a1,a2,a3},测试集为 T={t1,t2,t3,t4,t5,t6,t7,t8,t9,t10},系统工作模式集为 M={m1,m2},m1代表交流供电模式,此时 K1闭合,K2断开;m2代表直流供电模式,此时 K2闭合,K1断开.图略.

图2 某飞机供电系统的有向图模型Fig.2 Directed graph model of pow er supply system for an airplane

表1 案例系统在模式 m1下的相关性矩阵Tab.1 Dependencymatrix in themode m 1 for the case
根据有 AND节点的相关性矩阵的建立方法,无论在在模式 m1还是在 m2下,都只有第一类单故障和最小故障,最后所得 m1和 m2的相关性矩阵分别如表1和表2所示(分别利用文献 [14]的最小故障方法和文献 [14]的最小割集方法得到的相关性矩阵与表1和表2的结果相同,限于篇幅,这里不再罗列).由表1和表2可以看出,测试 t1,t2,t3,t4,t5,t7在 m1和 m2中具有相同的关联故障集,因此属于公共测试(这里假设同一测试在不同模式下测试费用相同);t6,t8,t9在 m1和 m2中的关联故障集不一样;t10只在 m2中,不在 m1中,因此应将 m1中的 t6,t8,t9以及 m2中的 t6,t8,t9,t10单独列在公共测试的后面,并标注工作模式;另外故障状态 B只在 m2中,合并到系统相关性矩阵中时,它与属于 m1的测试不相关,对应元素为 0.最后所得系统相关性矩阵如表3所示.在表1,表2,表3中,MF1和 M F2分别为系统的两个最小故障,其中,MF1={TD1,TD2},M F2={Z1,Z2,X1,X2}.

表2 案例系统在模式 m2下的相关性矩阵Tab.2 Dependency matrix in them ode m2 for the case

表3 案例系统的相关性矩阵Tab.3 The w hole dependency matrix of the case
5 结 论
由相关性模型生成相关性矩阵,对于复杂系统测试和故障诊断具有非常重要的意义.本文考虑了系统冗余、系统工作模式不单一的情况,提出了一种复杂系统相关性矩阵的生成新方法.
1)在存在冗余的情况下,本文将故障分为第一类单故障、第二类单故障以及最小故障而分别考虑,方便直观,不容易遗漏故障;特别是给出了第二类单故障的处理方法,这是现有方法未考虑的.
2)给出了系统在多种工作模式下,系统相关性矩阵的合并方法,解决了多模式系统的相关性矩阵的生成问题.
3)经过案例验证表明,利用本文的方法能够生成同时具有 AND节点和开关节点的复杂系统的相关性矩阵,为生成基于相关性矩阵的故障诊断策略奠定了基础,具有一定的工程实用价值.
[1] Sim pson W L,Sheppard JW.System comp lexity and integrated diagnostics[J].IEEEDesign&Test of Computers,1991,8(3):16-30.
[2] Deb S,Pattipati K R,Raghavan V,et al.Mu lti-signal flow graphs:a novel app roach for system testability ana lysis and fau lt diagnosis[C].AU TOTESTCON′94.IEEE Systems Readiness Technology Con ference,Anaheim,CA,1994:361-373.
[3] 杨智勇,许爱强,牛双诚.多信号模型的系统测试性建模与分析[J].工程设计学报,2007,14(5):364-368.
Yang Zhiyong,Xu Aiqiang,Niu Shuangcheng.Modeland analysis of system testability based on multi-signalmodel[J].Journal of Engineering Design,2007,14(5):364-368(in Chinese)
[4] Gou ld E.Modeling it both ways:hybrid diagnostic modeling and its app lication to hierarchical system designs[C].Autotestcon 2004,IEEE Proceedings,O range,CA,USA,2004:576-582.
[5] Pattipati K R,Alexand ridisM G.App lication o f heuristic search and in formation theory to sequential fault diagnosis[C].IEEE Transactions on Systems,Man,and Cybernetics,1990:872-887.
[6] Shakeri M,Raghavan V,Pattipati K R,et al.Sequential testing algorithms for multiple fault diagnosis[J].IEEE Trans On SM C 2000,30(1):1-14.
[7] 龙兵,王日新,姜兴渭.多信号模型航天器配电系统最优测试技术[J].哈尔滨工业大学学报,2005,37(4):440-443.
Long Bing,W ang Rixin,Jiang Xingwei.Op timal test techno logy for distribution systems o f spacec rafts based on multisignalmodel[J].Journalof Harbin Institute of Technology,2005,37(4):440-443.(in Chinese)
[8] 薛凯旋,黄考利,张玮昕,等.基于多信号模型的测试性分析与故障诊断策略设计[J].弹箭与制导学报,2008,28(4):225-227.
Xue Kaixuan,Huang Kaoli,Zhang W eixin,et al.Testability analysis and fault diagnosis strategy design based on mu lti-signalmodel[J].Journa l of Projec tiles,Rockets,Missiles and Guidance,2008,28(4):225-227.(in Chinese)
[9] 杨鹏,邱静,刘冠军.多故障诊断策略优化生成技术研究 [J].兵工学报,2008,29(11):1379-1383.
Yang Peng,Qiu Jing,Liu Guan jun.Research on optimization generation technology for mu ltip le fau lt diagnostic strategy[J].Acta Armamentarii,2008,29(11):1379-1383.(in Chinese)
[10] 景小宁,李全通,陈云翔,等.基于信息嫡的最少测试费用故障诊断策略[J].计算机应用,2005,25(2):417-419.
Jing Xiaoning,Li Quantong,Chen Yunxiang,et al.Information entropy-based fault diagnosis strategy with least test cost[J].Journa l o f Computer App lications,2005,25(2):417-419.(in Chinese)
[11] 连光耀,黄考利,赵常亮.复杂电子系统测点与诊断策略的优化方法 [J].系统工程与电子技术,2004,26(11):1739-1742.
Lian Guangyao,Huang Kaoli,Zhao Changliang.Efficient algorithm for test-node and diagnosis strategies of a comp lex elec tronic system[J].Systems Engineering and Elec tronics,2004,26(11):1739-1742.(in Chinese)
[12] 王子玲,许爱强,牛双诚.基于多故障假设的诊断策略研究与应用[J].工程设计学报,2009,16(4):281-285.
Wang Ziling,Xu Aiqiang,Niu Shuangcheng.Research and app lication on multip le fault diagnosis strategy[J].Journal of Engineering Design,2009,16(4):281-285.(in Chinese)
[13] 田仲,石君友.系统测试性设计分析与验证 [M].北京:北京航空航天大学出版社,2003.
[14] Shakeri M,Pattipati K R,Raghavan V,et al.Mu ltip le fault isolation in redundant systems[C].IEEE Autotestcon′95.System s Readiness:Test Technology for the 21st Century′.Conference Record.Atlanta,GA,1995:512-527.
[15] Pattipati T F,Deb K R S.et a l.Mu ltiple Fault Diagnosis in Graph-Based Systems[C].SPIE Conference on Fau lt Diagnosis,Prognosis and System Hea lth Management,O rlando,Floride,2002:281-322.
