基于滑模观测器的环形倒立摆控制系统的设计与实现❋
2010-02-09张昌凡黄宜山
邵 瑞,张昌凡,黄宜山,戴 璐
(湖南工业大学 电气信息工程学院 ,湖南 株洲 412008)
倒立摆系统作为典型的快速、多变量、非线性、绝对不稳定系统,一直是控制理论与应用的热点问题,不但是验证现代控制理论的典型实验装置,而且其控制方法和思路对处理一般工业过程亦有广泛的用途.又因其与火箭飞行器及单足机器人有很大的相似之处,引起国内外学者的广泛关注.其控制方法在军工、航天、机器人领域和一般工业过程中都有着广泛的用途.如机器人行走过程中的平衡控制,火箭发射中的垂直度控制和卫星飞行中的姿态控制等均涉及到倒置问题,对倒立摆系统的研究在理论和方法论上均有着深远意义.
目前对倒立摆理论方面的研究已经比较成熟,包括系统控制器的设计、自动起摆策略的研究及鲁棒性的探讨.典型的控制器设计理论有:PID控制、根轨迹以及频率响应法、状态空间法、最优控制理论、模糊控制理论、神经网络控制、拟人智能控制、鲁棒控制方法、自适应控制等以及这些控制理论的相互组合组成更强大的算法[1-5].起摆策略主要是基于能量的控制策略等[6-8].而这些方法的研究都是以状态变量全部可测为前提的,然而,实际系统的状态通常是未知或仅为部分可知的.如果仅靠仪器仪表或传感器等测量手段来获取控制系统所需要状态变量、系统参数等信息,不但要增大系统开支,也增加了硬件的复杂性,更何况有的信息本身就不便于或是无法通过物理测量获取.观测器可以根据系统模型从部分可测状态变量着手,重构出其它不可测的状态变量,因而采用观测器方法,可以在降低测量系统复杂性的基础上实现高性能控制器的设计,因此,状态观测器的设计是实现高精度控制的关键.
在此,应用拉格朗日方程方法建立了环形一级倒立摆的非线性数学模型,在应用控制理论分析的基础上,采用状态反馈的极点配置法为倒立摆系统建立了一种合适的控制方案,利用滑模控制有关理论设计了滑模状态观测器,并在实际的倒立摆系统中通过运动控制器实现了实时控制,取得了较好的控制效果.
1 系统描述
在忽略了空气流动,各种摩擦之后,可将倒立摆系统抽象成两个匀质杆和质量块组成的系统,如图1所示.其中,m1代表连杆的质量;m2代表摆杆的质量;m3代表质量块的质量;l1代表连杆长度;l2代表摆杆转动中心到杆质心的距离;θ1代表连杆与水平 x轴的夹角(顺时针为正);θ2代表摆杆与垂直向上方向的夹角(顺时针为正).
关于倒立摆运动方程的建立和分析,很多文献都有介绍,主要有牛顿-欧拉方法和拉格朗日方法.这里采用文献 [9]中介绍的利用拉格朗日方程推导环形倒立摆运动学方程的方法得到系统的运动方程.
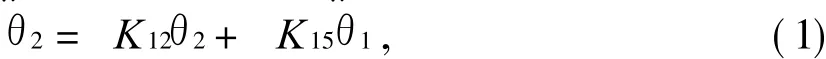
式中:K 12=3g/(4l2),K15=3l1/(4l2).采用角加速度作为输入,得到方程


图1 环形倒立摆系统示意图Fig.1 The sketch map of the circular inverted pendulum system
2 控制器的设计
由于倒立摆系统是一个单输入多输出的非线性绝对不稳定系统,采用经典控制方法的 PID和根轨迹等方法无法满足同时控制多个输出量的要求.故这里用 LQR的极点配置法设计控制器[10].
系统实际参数为 m1=0.234 kg,l1=0.221m,m2=0.13 kg,l2=0.197 5m,m3=0.178 kg,重力加速度取 g=9.8m/s2.代入式 (1)求 K12,K15得 K12=37.215 2,K 15=0.839 2.求出矩阵 A的特征值为0,0,6.100 4和 -6.100 4,有一个特征值大于 0,说明系统开环不稳定.由 rank([B A*B A^2*B
A^3*B])=4及 rank([C*B C*A*B C*A^2*B C*A^3*B D])=2可知系统可控可观,故可以对系统进行控制器设计,使系统稳定,同时可以设计状态观测器来求取系统中没有直接测量的速度变量.
在设计此控制器时,控制量 u=-K x,K为线性最优反馈增益矩阵.由系统可控,根据设计经验把极点配置在 p1=-3+2 j;p2=-3-2j;p3=-10;p 4=-20.用 Achermann算法配置闭环极点[11],调用 acker()函数,求得 K值为 K=[-69.863 9 595.899 8 -42.724 5 93.809 0].
实际中连杆和摆杆的角度是通过角度编码器采集数据实现测量,相应速度量可以通过加速度传感器来实现测量,也可以通过采用角度量的差分来近似速度量,因为光电码器的信号较为可靠.然而应用速度传感器增加了硬件设备,对角度量的微分不能避免噪声的干扰,使系统不稳定,因此考虑用滑模观测器来实现对未知变量即速度量的观测,这样既简化了系统硬件设备,又能避免系统噪声的干扰.
3 滑模观测器的设计
近年来,滑模变结构控制理论在解决复杂的非线性系统的综合问题时,取得了突出的进展.国内外对滑模变结构在状态观测器的应用已有一定的研究基础,相关方法相继被提出[12-15],本文采用文献 [14]所提滑模变结构观测器设计方法设计倒立摆系统中的观测器.
这里所设计的状态观测器,只需已知两个状态变量 x1,x2即可实现对其它两个状态变量 x3,x4的观测,因而在所研究的实际倒立摆系统中,仅需两个角度编码器可完成对系统数据的采集,而不需要测量速度的速度传感器,简化了系统的硬件需要.

4 系统实现及实验结果
4.1 倒立摆系统在 Matlab中的仿真


图2 Simulink仿真结果Fig.2 The results of sim ulation
通过对倒立摆系统控制器和观测器的仿真,验证了所提方法的有效性.并对倒立摆系统的非线性等特性有了比较深刻的理解,为进一步的实际试验奠定了基础.
4.2 倒立摆实时控制
环形倒立摆系统的系统框图如图3所示.
系统包括计算机、运动控制卡、伺服机构、电控箱、倒立摆本体和光电码盘几大部分,组成了一个闭环系统.光电码盘 1将连杆的角度、角速度信号反馈给伺服驱动器和运动控制卡,摆杆的角度、角速度信号由光电码盘 2反馈回控制卡.计算机从运动控制卡中读取实时数据,确定控制决策,并由运动控制卡来实现该控制决策,产生相应的控制量,驱动电机转动,带动连杆运动,保持摆杆的平衡.

环形倒立摆本体由基座、伺服机构、连杆、一级摆杆、二级摆杆、角度编码器等组成.其中伺服机构采用的是具有增量式编码器的交流松下伺服电机.控制伺服电机时,控制器输出 + /-10 V模拟电压控制信号.电机型号是 MSMD022P1U,功率 0.2 kW,转速3 000 r/min.电控箱内安装有交流伺服驱动器、I/O接口板、开关电源、开关和指示灯等电气元件.

图4 实际倒立摆系统组成Fig.4 The real circular inverted pendulum system
控制平台主要组成部分:与 IBM PC,AT机兼容的 PC机、GT-400-SV PCI运动控制卡、运动控制卡用户接口软件.这里运动控制卡核心由 ADSP2181数字信号处理器和 FPGA组成,可以实现高性能的控制计算.GT系列运动控制器提供 C语言函数库和W indows动态链接库,实现复杂的控制功能.并具有可编程事件中断;可设置跟随误差极限、加速度极限、控制输出极限等,保证控制安全可靠及硬件捕获原点开关和编码器 Index信号,实现高精度机器原点位置锁存.倒立摆实际系统组成如图4所示.
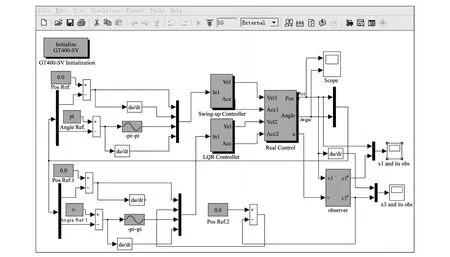
图5 环形倒立摆系统实时控制程序图Fig.5 The real-time control program of the circular inverted pendulum
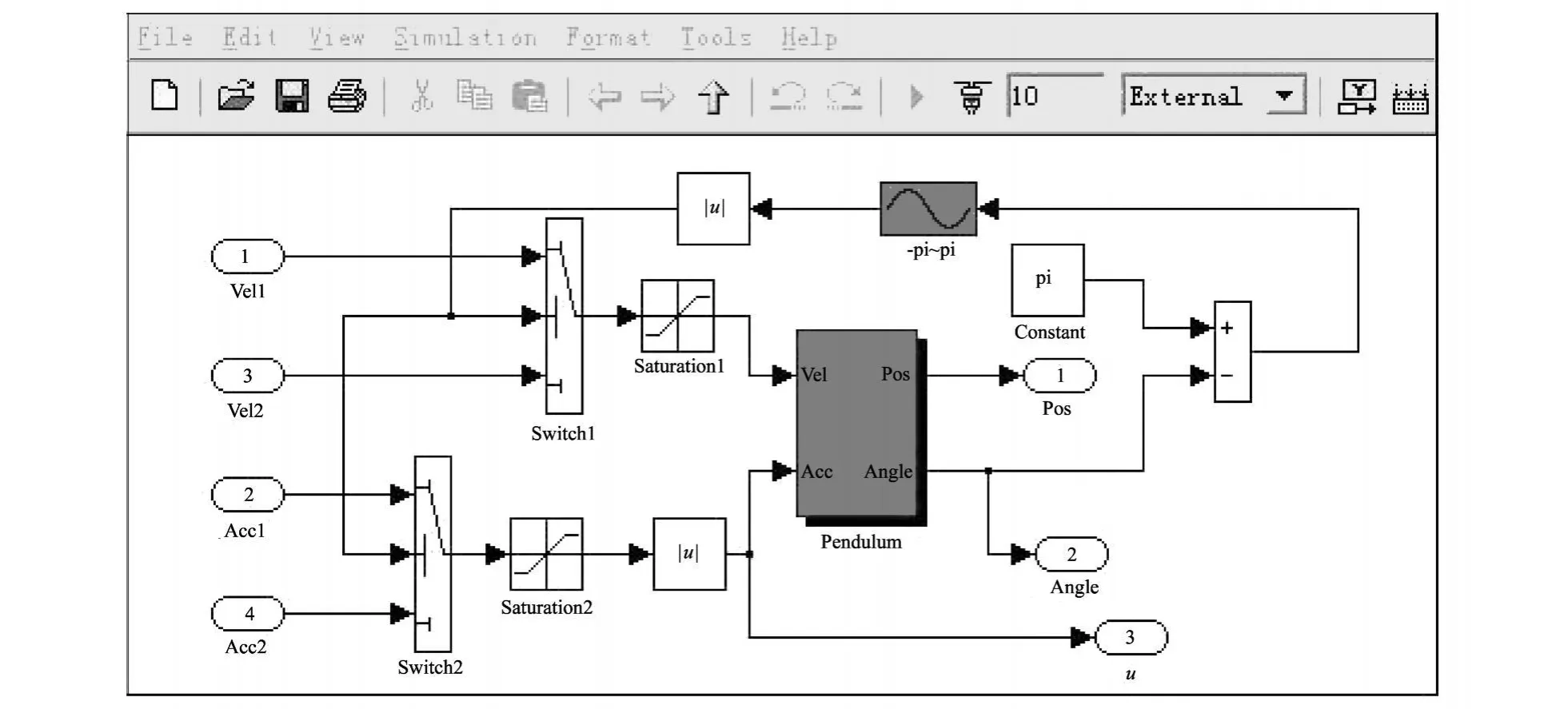
图6 实时控制子系统程序图Fig.6 The Real control subsystem program
实际控制时,通过把 Matlab 7.1中 Simu link程序编译到 RTW(Real-TimeW orkshop 6.3)实现对系统的实时控制[16].同时利用 VC++ 语言作为编译和运行的环境.利用 Simulink建立的倒立摆系统模型主界面如图5所示,Real Control子系统程序框图如图6所示,其中 Pendulum为倒立摆实际控制对象;observer为滑模观测器子系统,程序如图7所示.

图7 观测器子系统程序图Fig.7 The observer subsystem p rog ram

图8 系统实际控制输出结果Fig.8 The results of real-tim e control system
编译程序下载到运动控制卡中,采样周期设置为 0.005 s,这里运动控制卡采用的是深圳固高科技有限公司的 GT系列的 GT-400-SV-PCI板卡,然后运行程序使系统达到稳定,利用 x PC Target for Scope获取实验输出波形如图8所示.由图8(a),8(b)可知程序执行前 6 s是基于能量控制的自动起摆过程,6~9 s是自动起摆到稳摆控制的过渡过程.第 7 s左右是程序从自动起摆到稳摆控制的切换运行.从图8(c)和 8(d)中可看出第 9 s时系统到达稳定状态,连杆稳定在相对参考位置的 -0.025 rad的位置,摆杆处于动态平衡状态,稳定到相对参考位置 3.14 rad的位置.同时状态变量x3实现了很好的跟踪.
由以上倒立摆系统的仿真和实际控制结果可以看出,仿真中各加速度变量的观测值收敛到零,实现系统的稳定控制.在实际的倒立摆控制系统中,连杆和摆杆的角度能实现动态的稳定,其各自的加速度量也稳定在零点附近.其中连杆的加速度观测值能跟踪上实际值.
5 结 语
本文针对环形倒立摆系统的控制,分别基于最优控制理论和滑模控制理论设计系统的控制器和状态观测器.在保证控制器实现对系统控制的情况下,引入滑模状态观测器实现对未知变量的观测,简化了系统硬件,减少了系统对外界噪声的影响.仿真表明了该观测器方法的可行性,实际倒立摆控制验证了该方法的实用性和有效性.
[1] Zhao J,Spong M W.Hybrid contro l for globa l stabilization of the cart-pendu lum system[J].Automatica,2001,37(12):1941-1951.
[2] Cho H T,Seul J.Neural netw ork position tracking contro l of an inverted pendu lum an X-Y tab le robot[J].Intelligent Robots and Systems,2003,2:1210-1215.
[3] Marzi H.Multi-Input Fuzzy control of an inverted pendulum using an armature controlled DCmotor[J].Robotica.2005,23(6):785-788.
[4] 李铁龙.非线性滑模变结构控制及其在倒立摆系统中的应用研究[D].秦皇岛:燕山大学,2005.
[5] Yang JH,Shim SY,Seo J-H,et al.Swing-up control for an inverted pendu lum with restricted cart rail length[J].Int.Journal o f Control,Automation and Systems,2009,7(4):674-680.
[6] Yoshida K.Sw ing-Up Controlofan Inverted Pendulum by Energy-Based Methods[C].Proceedings of the American Control Conference,1999:4045-4047.
[7] Astro m K J,Furuta K.Swinging up a pendulum by energy contro l[J].Automatica,2000,36(2):287-295.
[8] Muskinja N,Tovornik B.Swinging up and stabilization of real inverted pendulum[J].IEEE Trans.on Industrial Electronics,2006,53(2):631-639.
[9] 吴爱国,张小明,张钊.基于 Lagrange方程建模的单级旋转倒立摆控制[J].中国工程科学,2005,7(10):11-15.
W u Aiguo,Zhang Xiaom ing,Zhang Zhao.A contro l system based on the lagrangemodeling method for a sing le link rotary inverted pendulum[J].Engineering Science,2005,7(10):11-15.(in Chinese)
[10] 张小明.旋转倒立摆系统控制方法的研究[D].天津:天津大学,2005.
[11] 姚胜兴,彭楚武.基于比例切换变结构控制的倒立摆系统研究[J].武汉理工大学学报,2007,29(4):114-117.
Yao Shengxing,Peng Chuw u.Research on inverse pendulum system based on proportion switching variab le structure control[J].Journalof W uHan University of Technology,2007,29(4):114-117.(in Chinese)
[12] Tan C P,Edw ards C.Sliding mode observers for detec tion and reconstruction o f sensor fau lts[J].Automatica,2002,38(5):1815-1821.
[13] Edw ards C,Spurgeon S K.On the development of discontinuous observers[J].International Journal o f Contro l,1994,59(5):1211-1229.
[14] Fabienne F P.Francoise L L.State and parameter identification for nonlinear uncertain systems using variable structure theory[C].The 4th W orkshop o f the Non linear Contro l Netw ork,2001,Berlin/Heidelberg:Springer,2003:109-128.
[15] 何静,邱静,张昌凡,王锡波.非线性系统的集成故障诊断和容错控制 [J].机械工程学报,2009,45(5):70-78.
He Jing,Qiu Jing,Zhang Chang fan,Wang Xibo.Integrated fau lt diagnosis and fau lt-to lerant contro l for nonlinear system[J].Journalof Mechanical Engineering,2009,45(5):70-78.(in Chinese)
[16] Sukontanakarn V,Parnichkun M.Real-timeop timal control for rotary inverted pendulum[J].American Journa l of App lied Sciences,2009,6(6):1106-1115.
