基于最小二乘法的多频涡流检测信号参数分析❋
2010-02-09高军哲潘孟春罗飞路
高军哲,潘孟春,罗飞路
(国防科技大学 机电工程与自动化学院 ,湖南 长沙 410073)
0 引 言
1970年,美国科学家 Libby首先提出了多频涡流检测是实现多参数检测的有效方法[1].多频涡流检测技术应用到核电站蒸汽发生管道的役前和在役检测,有效地消除了支撑干扰信号[2].在多频涡流检测中,电涡流传感器被几个频率的正弦信号激励,经过平衡电桥和被检测对象耦合.如何有效地提取多频激励条件下每个频率分量的参数是多频涡流检测系统的关键.一般采用带通滤波器和模拟相敏检波的方法进行检测,或者采用数字相敏检波的方法,这两种方法对电路设计有特定的要求,检测系统的硬件成本较高,且检测系统参数不易调节.1809年,高斯在书中详细描述了最小二乘方法[3].最小二乘法在数字信号处理、图像识别、目标跟踪领域得到了广泛应用[4].本文将最小二乘法应用于多频涡流检测信号的特征参数提取和分析.
1 多频涡流检测系统信号特征
1.1 多频涡流检测原理
当电涡流传感器(线圈结构)放置于待测金属导体上方,线圈中通以多频交变电流,将会在金属导体近表面激发感应涡流,如图1所示.

图1 多频涡流检测示意图Fig.1 Diagram of M FECT

图2 多频涡流检测的变压器等效电路Fig.2 Equivalen t transformer circuit of M FECT
针对多频涡流检测系统,其变压器耦合等效电路如图2所示.电路中有两个相互耦合的线圈 L1和L2,R1和 L1代表检测线圈的电阻和电感,R2和 L2代表被测金属导体的等效电阻和等效电感.原边回路的视在电阻和视在电感的变化与金属导体的表面状态、检测频率 f、金属导体的电导率e和耦合系数 M等有关.
视在电阻和视在电感的变化在电路中反应为电压和电流的幅值和相位的微弱变化,一般通过电桥和放大技术实现对检测线圈输出信号的放大.电桥和电磁耦合均为线性系统,所以在每个频率下的响应变化等于各个单独频率下响应变化的合成.
1.2 多频涡流检测信号特征
假定多频涡流检测系统的线圈传感器激励频率为两种,且激励频率 f1和 f1为已知信号,则可以通过采集线圈传感器的输出信号,并以两路激励正弦信号作为参考,求解线圈传感器输出信号在每个频率分量下的幅值和相位变化.
因此,在多频涡流检测系统要实现两种信号的检测,必须对一种已知频率的单频正弦信号的幅值和相位进行检测,对另一种已知频率的多频正弦信号的幅值和相位进行检测,本文以双频涡流检测系统为例进行算法设计.
2 多频涡流信号分析算法设计
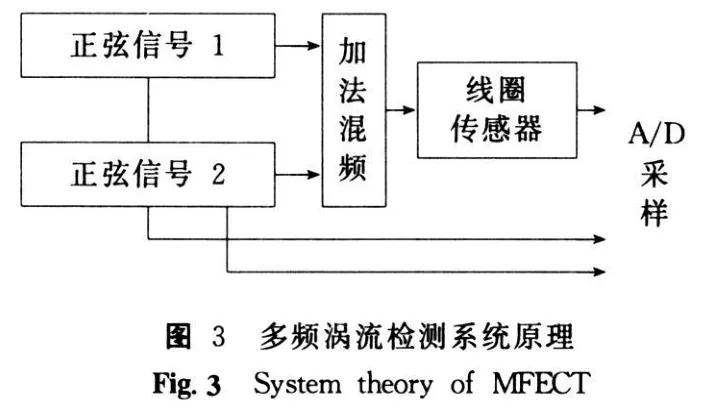
假设分别有多频涡流检测信号g s(t)和参考信号g r1(t)和g r2(t),已知信号角频率为k 1和k 2.在涡流检测信号分析中,参考信号的幅值 Vr和相位h r为固定不变参数,涡流检测信号的幅值 Vs1,Vs2和相位h s1,h s2相对参考信号的变化可以用来评估被检对象的状态信息.多频涡流检测系统各信号表示如下:
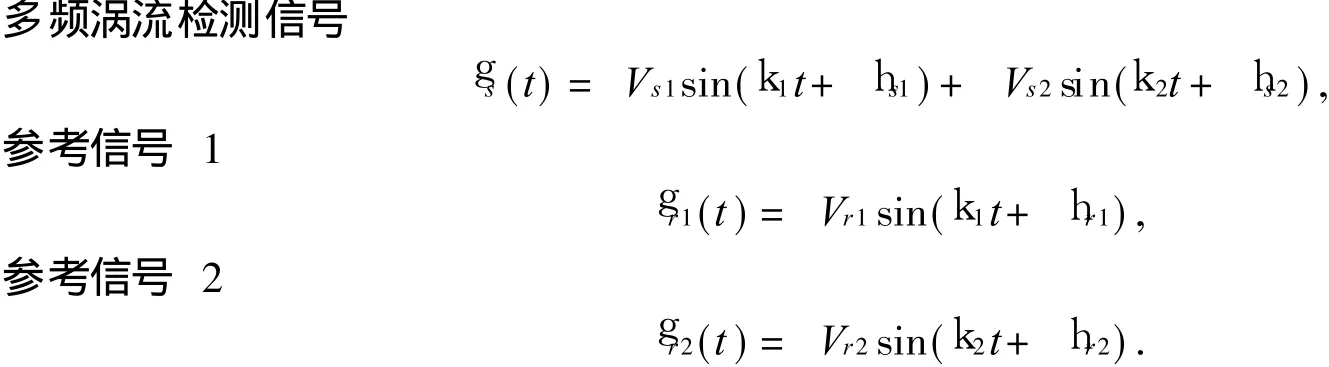
2.1 单频正弦信号特征参数分析算法
针对单频参考信号g r(t)=Vr sin(k t+h r),信号频率为k.对其展开并线性化

式中:V1=Vr cos h r;V2=Vr sin h r.
则单频信号的幅值和相位可表示为

为了确定 V1,V2,采用最小二乘法进行估计.根据 V1,V2参数总的测量残差平方和最小,用求导数的方法得到其最小二乘估计.
在采样频率 fs已知的情况下,采样间隔Δ=1/fs,对信号进行采样,得到 M个采样值g r(nΔ),其中,n=1,2,… ,M,则测量残差可表示为

若 ATr A r为非奇异矩阵,则 V r必有唯一解,其矩阵表达式为

2.2 多频正弦信号特征参数分析算法
针对多频涡流检测信号,不妨假定其为双频信号,信号频率为k1和k2.信号可表示为
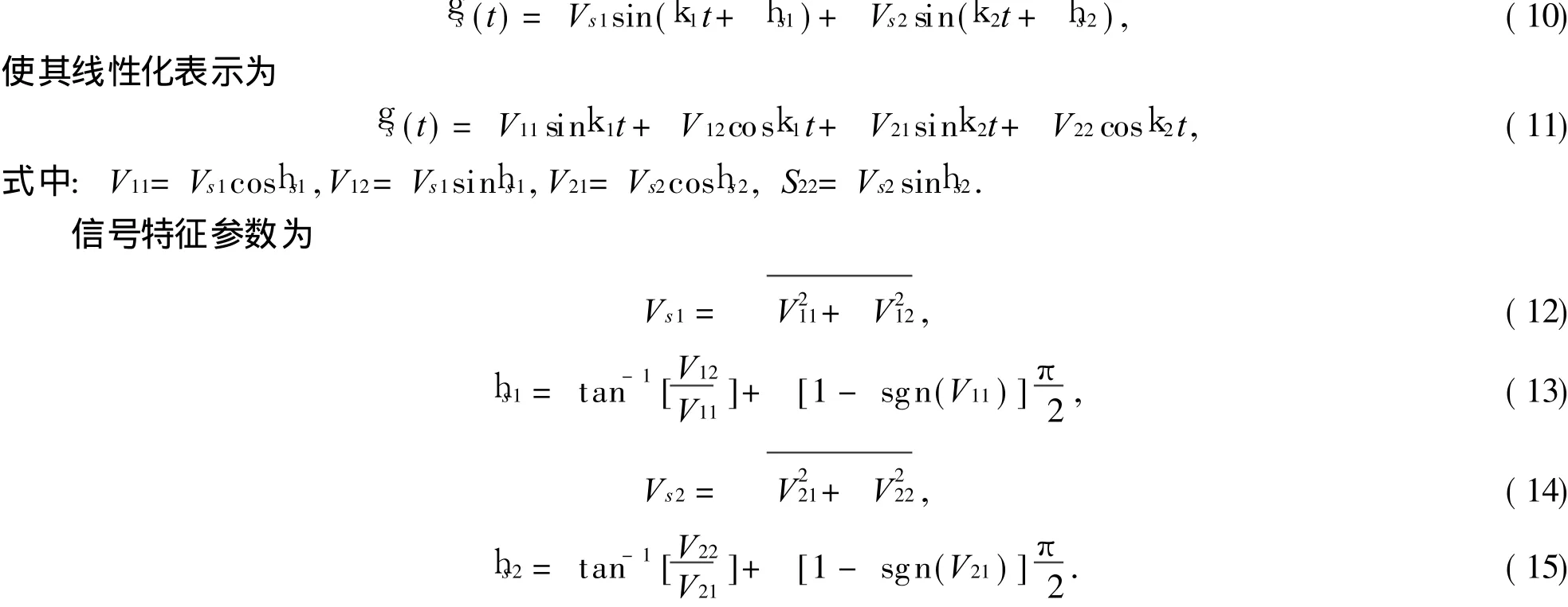
仿照 2.1节的过程,根据最小二乘法的要求,推导过程如下:
在采样频率 fs已知的情况下,采样间隔Δ=1/fs,对信号进行采样,得到 M个采样值g s(nΔ),其中,n=1,2,…,M,则测量残差可表示为
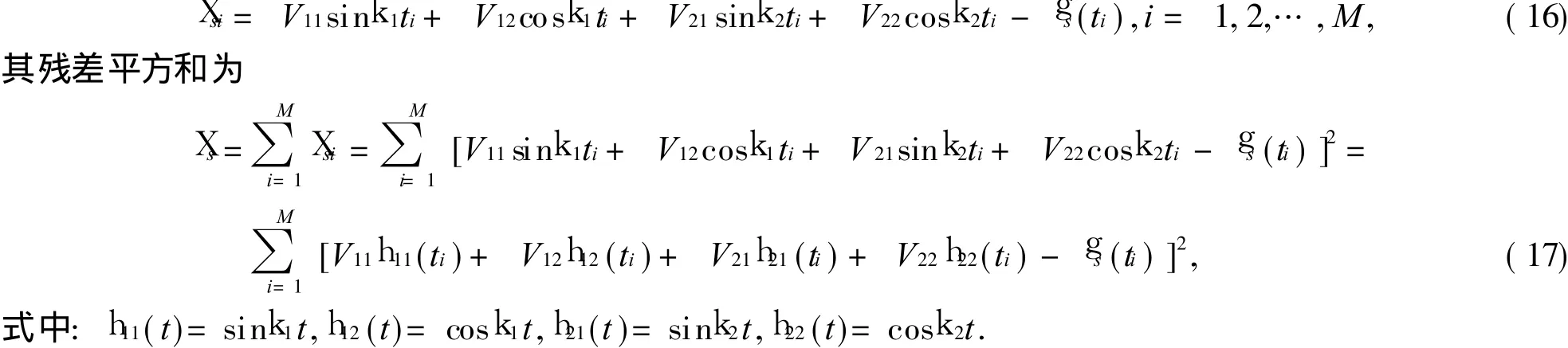
根据最小二乘原理,有极小值存在的必要条件,分别求对 Vjk的偏导数,并令其为零,有

2.3 分析算法的软件实现
对于双频涡流检测系统,已知参数为涡流检测的信号频率 f1和 f2、采集频率 fs.首先,确定采样点数 M,计算矩阵 A r和 A s.其次,在检测过程中,通过三路 A/D同步采集两路参考信号和涡流检测信号,提取 M点采样值,求解向量 V r和 V s.然后,根据向量 V r和 V s求解每个频率分量下正弦信号的幅值和相位变化,分析检测对象的特征变化.
3 实验结果
为了验证分析算法的可靠性,本文分别进行仿真实验和涡流检测实验.
3.1 仿真实验
仿真实验利用 Matlab7.0进行,选取双频检测信号的检测频率分别为 f1=5 k Hz和 f2=10 k Hz,采集频率 100 kHz,产生仿真信号并加入噪声干扰.仿真实验结果见表1~表3.
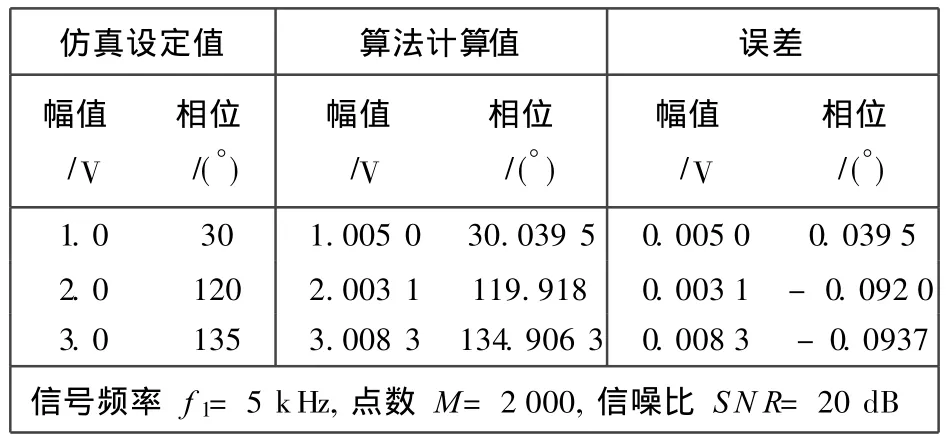
表1 单频仿真实验结果Tab.1 Simulation result of single frequency
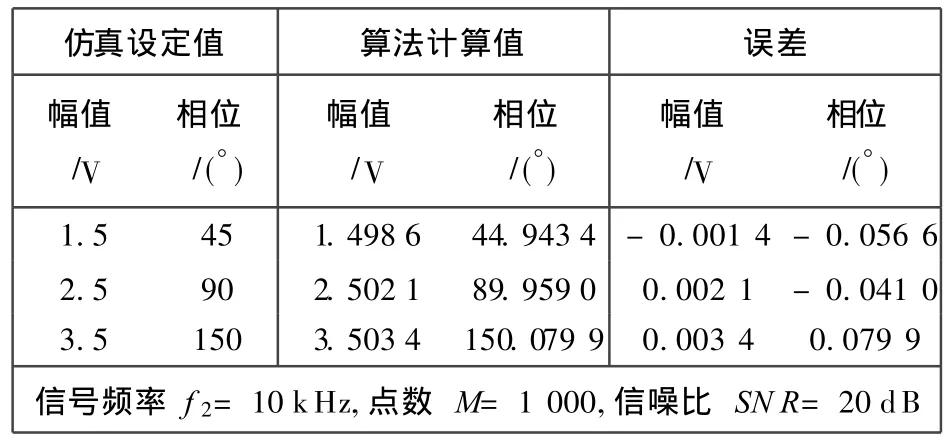
表2 单频仿真实验结果Tab.2 Simulation result of single frequency

表3 双频仿真实验结果Tab.3 Simulation result of dual-frequency
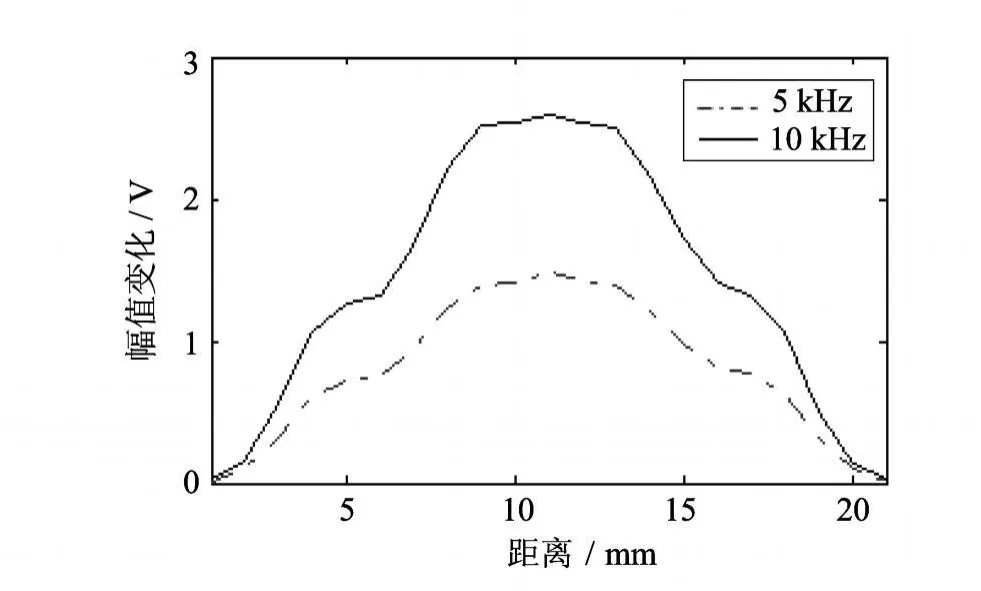
图4 线圈传感器经过缺陷时幅值变化Fig.4 Am plitude variation of a p robe-coil passing defects
从仿真结果可以看出,该算法可以有效地检测单频信号和多频信号的幅值和相位,并有较高的检测精度,检测相对误差小于 1%.
3.2 涡流检测实验
基于该算法,在涡流检测系统中对线圈传感器经过缺陷时的信号幅值变化进行参数检测.可以看出,10 kHz检测信号的幅值变化大于 5 k Hz检测信号的幅值变化,在两种频率下分别检测到了缺陷,对缺陷信号进行处理,可以实现多参数检测和消除干扰信号(如提离、支撑物等).实验表明:算法具有较好的多频涡流信号参数检测能力.
4 结 论
传统的多频涡流检测系统一般采用带通滤波器和锁定放大器实现微弱涡流信号的检测.尽管锁定放大器具有较高的微弱信号检测精度,但是随着涡流检测系统频率的增加,硬件成本较高,且带通滤波器的中心频率一旦设定不易调节.基于最小二乘法的多频涡流检测信号分析系统在精度要求不高的场合(或者前端对涡流检测信号进行充分放大),大大减小硬件成本,且应用灵活.实验结果表明,在涡流检测信号经过放大之后,该算法可以有效地分析涡流检测信号的参数变化特征,可以应用到多频涡流无损检测的信号参数分析中.
[1] Libby H L.Introducion to elec tromagnetic nondestructive testmethods[M].New York:Johc W iley&Sons Inc,1971.
[2] 任吉林.流检测技术近 20年的进展[J].无损检测,1998,20(5):121-128.
Ren Jilin.Development of eddy current testing in recent twenty years[J].Nondestruc tive Testing,1998,20(5):121-128.(in Chinese)
[3] Sorenson HW.Least-squres estimation:from Gauss to Kalman[J].IEEE Spectrum,1970,7:63-68.
[4] Gozzo F.Recursice least-squares sequence estimation[J].IBM J.Res.Develop.,1994,38(2):131-156.
[5] Yin W,Dickinson S J,Pey ton A J.A multi-frequency im pedance analysing instrument for eddy current testing[J].Measurement Science and Technology,2006,17:393-402.
[6] Roberto Micheletti.Phase ang le measurement betw een tw o sinusoidal signals[J].IEEE Trans.Instru.Meas.,1991,40(2):40-42.
[7] Sachdev M S,Giray M P.A least error squares technique for determ ining power system frequency[J].IEEE Trans.Pow er App.Syst.,1985,104:437-443.
[8] 孙进才,朱维杰,孙轶源,等.正弦信号参数估计的最小二乘算法[J].哈尔滨工程大学学报,2005,26(1):19-23.
Sun Jincai,Zhu W eijie,Sun Yiyuan,et al.Method of least squares of parameter estimation for sinusoidal signals[J].Journal of Harbin Engineering University,2005,26(1):19-23.(in Chinese)
[9] 梁志国,朱济杰,孟晓风.四参数正弦曲线拟合的一种收敛算法[J].仪器仪表学报,2006,27(11):1513-1519.
Liang Zhiguo,Zhu Jijie,Meng Xiao feng.Convergence algorithm of four-parameter sine wave curve-fit[J].Chinese Journal o f Scientific Instrument,2006,27(11):1513-1519.(in Chinese)
[10] 张继龙,甄蜀春,曹鹏,等.实验数据的曲线拟合方法及其应用 [J].测试技术学报,2003,17(3):255-257.
Zhang Jilong,Zhen Shuchun,Cao Peng,et al.Research and app lication o f a new method fo curve fitting[J].Journal of Test and Measurement Techno logy,2003,17(3):255-257.(in Chinese)
[11] 吴义华,杨俊峰,程敬原,等.正弦信号四参数的高精度估计算法[J].中国科学技术大学学报.2006,36(6):625-629.
Wu Yihua,Yang Junfeng,Cheng Jingyuan,etal.High-accuracy estimation algorithm for 4 parameters of sne-w ave[J].Journal of University o f Scienceand Technology o f China,2006,36(6):625-629.(in Chinese)
