Bi2Te3纳米薄膜单轴拉伸的分子动力学模拟

童 宇, 易法军， 刘立胜， 张清杰

(武汉理工大学 a.材料复合新技术国家重点实验室； b.理学院， 湖北 武汉 430070)

热电材料是一种将热能和电能直接转换的功能材料，在温差发电和热电致冷等领域具有极为重要的应用前景。Bi2Te3基化合物是室温附近性能最好的热电材料。随着纳米研究技术的发展，近年来有关低维Bi2Te3材料取得高热电优值的报道不断出现[1,2]。由于薄膜材料的热电性能与块体材料有所不同，Bi2Te3薄膜有较高的研究价值。人们在研究Bi2Te3纳米薄膜材料的过程中探索了包括电化学沉积法在内的诸多合成制备方法，并广泛地关注其热学和电学特性[3～5]。目前对热电材料的研究仍主要集中在热电性能，但是材料的力学性能对其服役行为与使用寿命具有重要的影响，然而对于Bi2Te3薄膜材料力学性能的研究几乎处于空白状态。另外由于Bi2Te3热电材料在实际应用中不可避免地要经历较大的温度波动，研究材料的力学性能随温度的变化关系具有重要意义。因此对Bi2Te3纳米薄膜材料力学性能的研究非常重要。但是由于纳米尺度实验本身存在一定困难，而分子动力学方法能从微观研究材料原子运动过程和结构力学变形细节，另外由于分子动力学方法能够考虑温度效应，有助于人们对不同温度下材料的力学行为进行预测。因此从原子、分子尺度来考察材料的结构和特性的分子动力学模拟方法成为一种重要的研究手段，并取得了许多重要的进展。例如Yang等人利用MAEAM势计算了Nb(110)薄膜的熔点、熔化机制以及相应的动力学行为[6]。Cao等人利用分子动力学研究了不同厚度、取向和加载方向对ZnO纳米薄膜弹性性能的影响[7]。

本文用分子动力学方法模拟了单晶Bi2Te3薄膜沿其力学性能较弱的c轴方向的单轴拉伸过程。首先通过对系统的弛豫获得了无初应力以及能量最小化的稳定状态模型。在此基础上考察了微观尺度上薄膜材料整体的变形演化过程，得到了拉伸过程中能量、应力的变化曲线。模拟不同温度下的拉伸，分析温度效应对其力学性能的影响。当前研究结果为研究Bi2Te3纳米薄膜材料器件提供了有效的依据。

1 分子动力学模拟方法

分子动力学模拟是计算经典多粒子体系的一种有效方法，计算整体系统的力学行为和性能，是纳米计算力学的重要工具。模拟系统中的粒子运动符合经典的牛顿方程，即

(1)

其中原子i所受的力可以直接由势能函数U对坐标ri的一阶导数得到。因此原子间相互作用的描述方式是分子动力学模拟计算结果精确与否的关键。本文选用的Huang和Kaviany等人发表的Bi2Te3的多体势。该势函数最初用于计算Bi2Te3的晶格热导率[8]，势参数由第一性原理计算以及实验参数拟合而来。利用该势函数我们曾计算了Bi2Te3材料从0到600 K温度范围内的力学性质[9,10]。Bi2Te3多体势函数的具体形式为：

Etotal=Eelectr+Ebond+Eangle

(2)

其中Eelectr为静电势能，表达式为：

(3)

Ebond为Morse型键伸缩势能，表达式为：

Ebond=D{[1-exp(-α(r-r0))]2-1}

(4)

Eangle为三体键角弯曲势能，表达式为：

Eangle=K[cos(θ)-cos(θ0)]2

(5)

势函数具体参数详见参考文献[8]。

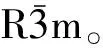
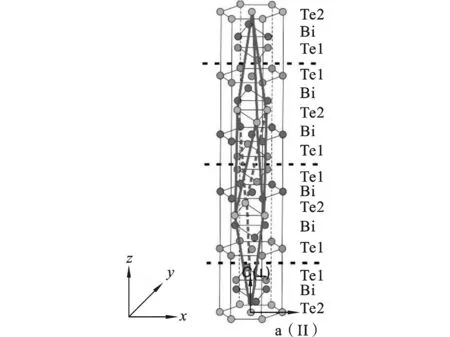
图1 Bi2Te3晶体结构与坐标系

图2 薄膜初始模型

模拟之前，先将Bi2Te3的纳米薄膜模型置于设定的温度中，并按照Maxwell-Boltzmann分布对原子赋予初始速度。然后将系统弛豫100皮秒(ps)，在此过程中利用Berendsen恒压算法使x和z方向的压力保持为0 Pa，同时利用Nose-Hoover热浴算法使系统的温度保持在特定值，以使系统初始应力为0 Pa。模拟时间步长设为1飞秒(fs)。弛豫过程完成后进行沿z轴单轴拉伸，在此过程中Berendsen压力控制仅限制在x方向。为了模拟真实的拉伸试验，在拉伸过程中模型一端固定而另一端原子沿z轴即[0 0 1]晶向运动。拉伸应变率设定为1×107s-1。拉伸过程中每施加0.001的应变系统弛豫2000步，以使系统原子回到平衡态，然后再施加应变，如此重复施加应变-弛豫的过程，直到模型发生破坏。本文中采用Verlet算法的速度形式对系统运动方程进行力学时间积分计算。模拟过程中每隔5000步输出原子的位置、应力分量、总能量、势能、动能等参数。模拟过程中应力的计算方法采用Virial算法。论文中所有模拟过程均利用LAMMPS分子动力学软件完成[11]，原子构型的显示使用VMD软件[12]。

2 模拟结果与讨论

拉伸模拟之前，先对系统进行一个趋衡过程即弛豫过程。这一步骤可以使系统达到初始平衡状态，同时消除初始速度带来的随机因素，以及自由表面的引入对纳米薄膜的影响。图3表示了Bi2Te3纳米薄膜在300 K时系统总势能、应力以及温度随着驰豫时间步的变化曲线。从图3(a)可以看出，在弛豫初期，系统的总能曲线经过一段时间的驰豫之后，达到一个稳定位置。图3(b)显示在初始状态，系统的初应力很大，约为-1.5 GPa。经过一段时间的弛豫后，应力值保持在零点附近，说明弛豫后薄膜整体是一个无外力的平衡体系。图3(c)表示温度经过多次震荡后，在4万步左右进入一个相对稳定的状态，达到所设定的值。以上3幅图可以看出，系统在经历驰豫过程之后达到平衡态。

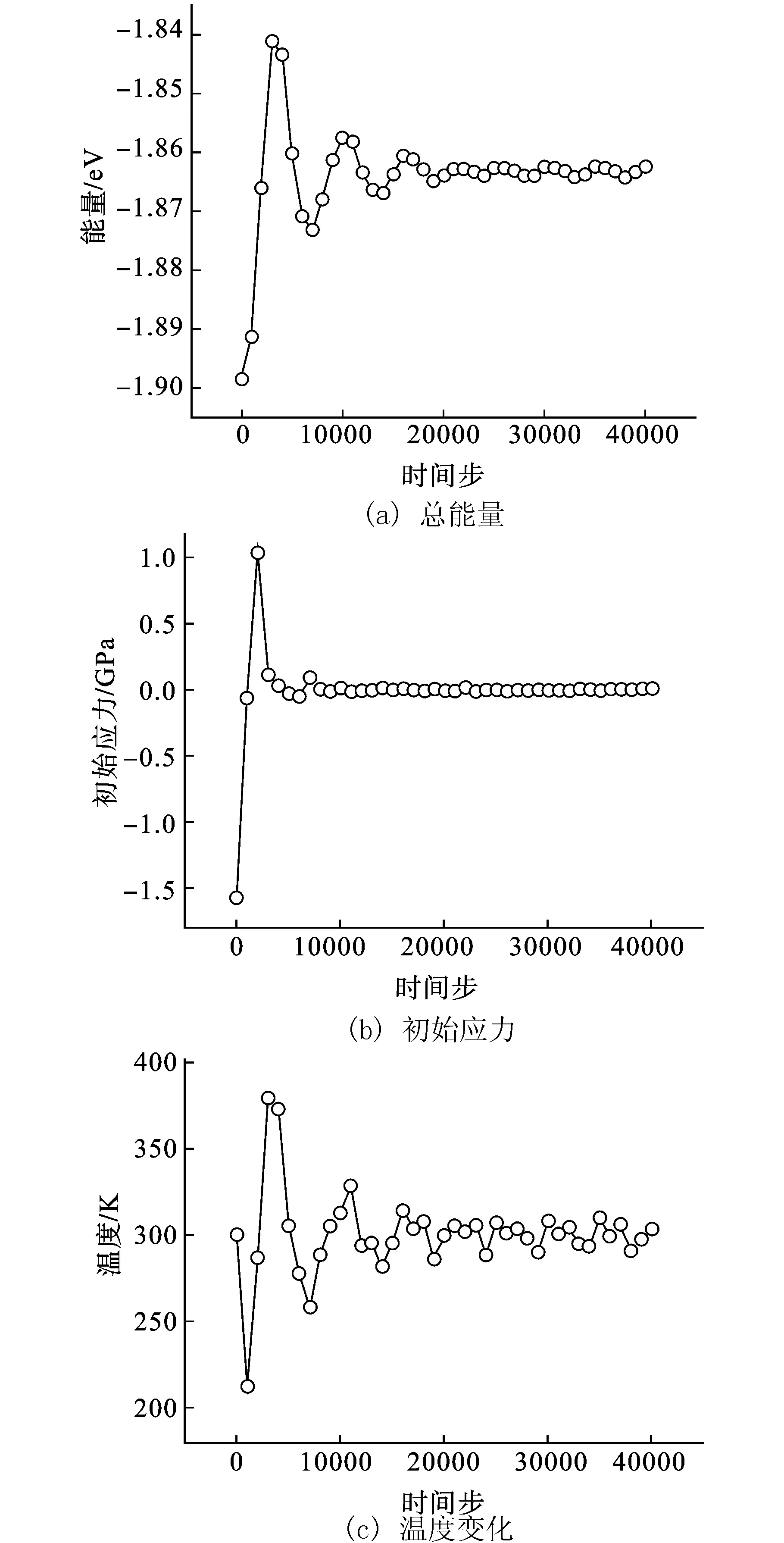
图3 弛豫过程中

图4为拉伸过程中的原子构型。可见拉伸变形初期，Bi2Te3纳米薄膜的原子排列规则(图4(a)，(b))。随着应变的逐渐增加，没有出现比较明显的原子滑移或错位现象。这种原子整齐排列的状态一直持续在整个拉伸过程，直到应变值达到0.048后，薄膜沿相邻Te1-Te1层间(0 0 1)晶面突然发生断裂并分离，断裂截面平整(图4(c))。这种断裂形式与块体相似。根据Drabble等人提出Bi2Te3的成键模型[13]。相邻层Te1-Te1之间的相互作用比较弱，几乎没有电荷作用。Te1原子的价电子都只与近邻的Bi原子成键，所以Te1-Te1之间表现为较弱的范德华相互作用，比离子键或者共价键弱(但比惰性气体如Kr-Kr或Xe-Xe的范德华键能略高)[8]。因此Bi2Te3晶体极易沿此晶面发生破坏。

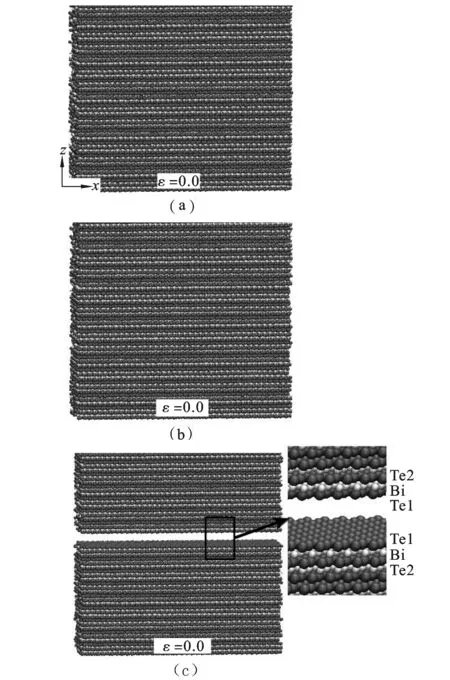
图4 Bi2Te3薄膜c轴方向单轴拉伸结构演化

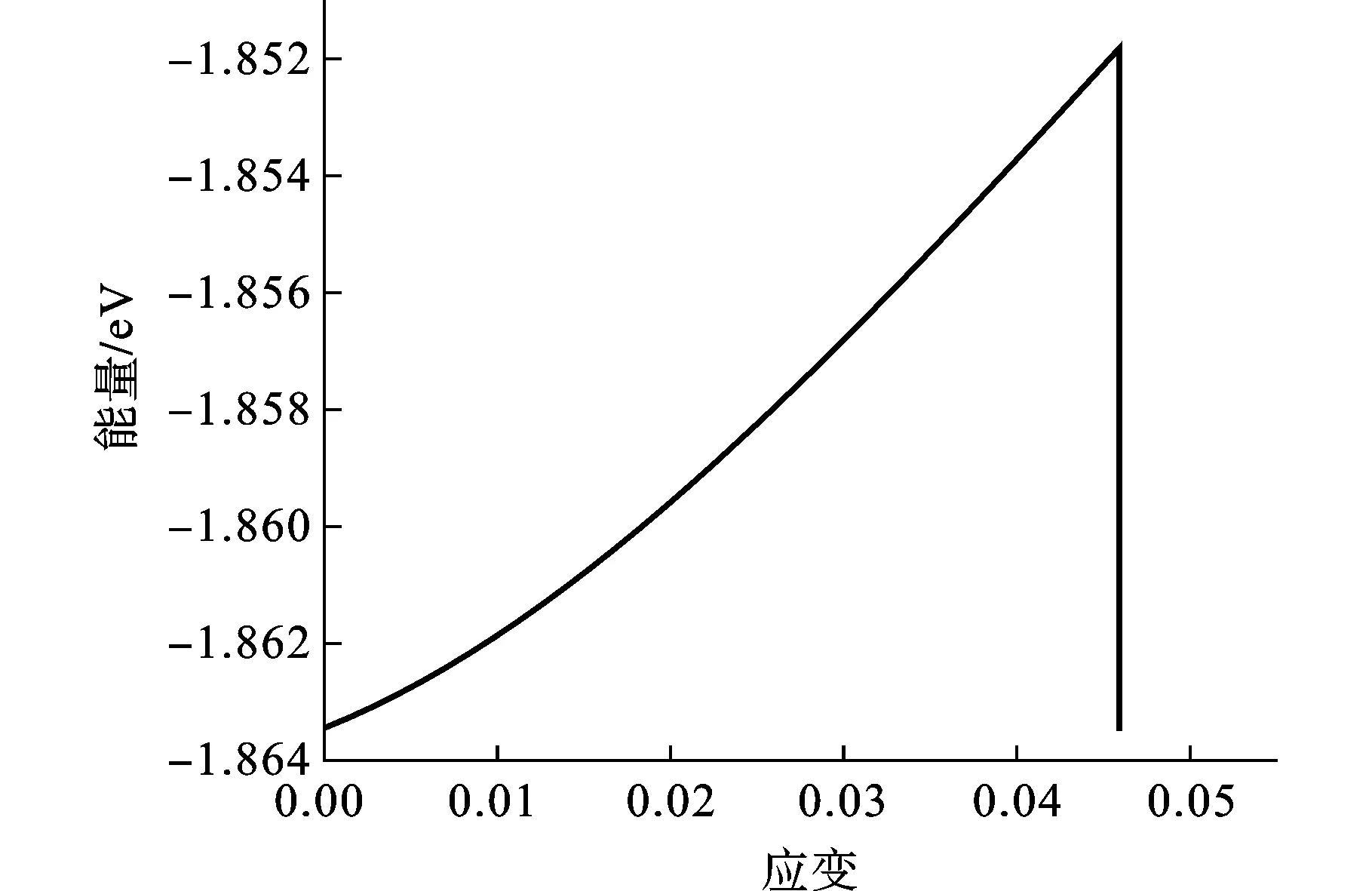
图5 原子能量-应变曲线

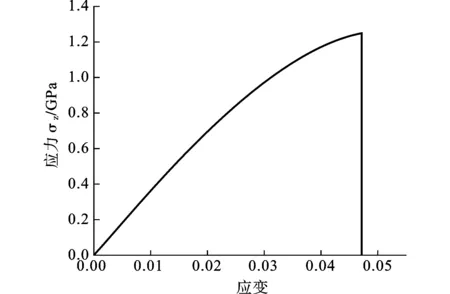
图6 应力-应变曲线

图5和图6分别为Bi2Te3纳米薄膜300 K时沿c轴方向拉伸的系统能量-应变和应力-应变曲线。由于在分子动力学模拟过程中，系统能量的变化趋势可以体现材料变形的特征，因此结合系统能量的变化曲线进行说明。由图6可以发现，初始阶段的应力应变曲线为线性变化，应力随着应变的增加而增加，模型中的原子逐渐偏离原来的理想位置，对应系统总能量也逐渐上升。随着拉伸应变的增大，原子间距逐渐增大，原子的运动也逐渐加剧，原子能量上升的速度也随之增大，从而导致体系能量急剧升高(图5)。当应变值达到0.03后，应力应变曲线变得略微平坦，表现出非线性特点。当应变达0.048后，随着应变的进一步增加，应力急剧下降到0，说明此时Bi2Te3纳米薄膜已经破坏。由能量-应变曲线可以看出，由于原子间相互作用此时急剧减小，系统势能得到释放，导致总能量降低。由应力-应变曲线以及拉伸过程中的原子构型变化可以看出Bi2Te3纳米薄膜沿c轴方向拉伸的破坏形式表现为明显的脆性断裂的特征。

根据以前对Bi2Te3薄膜沿a轴方向的研究[10]，比较两个主轴方向的Bi2Te3薄膜拉伸过程，发现两方向上共同的特点是拉伸初始阶段应力应变几乎呈线性变化，表现为脆性断裂。但是沿c轴的断裂由于直接发生在作用较弱的相邻层Te1原子之间，因而从强度值上两者相差较大，表明Bi2Te3纳米薄膜具有明显的各向异性的特点。

图7为0～600 K温度下Bi2Te3纳米薄膜沿c轴方向拉伸的应力应变曲线。可见随着温度的升高应力应变曲线的斜率逐渐降低。极限强度和破坏应变也随之降低。其中拟合的弹性模量(应变为0.01)从0K时的42 GPa下降到 600 K时的31 GPa，下降幅度为26%。极限强度从0K时的1.5 GPa下降到 600 K时的1.04 GPa，下降幅度为30%。破坏应变从0 K时的0.051下降到 600 K时的0.043，下降幅度为15%。

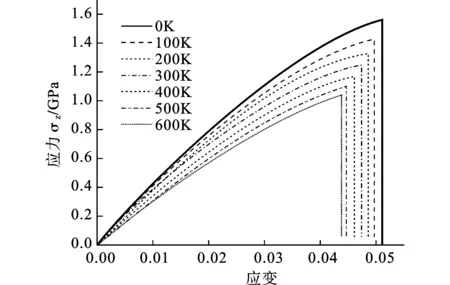
图7 不同温度下的应力-应变曲线

3 结 语

本文根据Huang和Kaviany提出的Bi2Te3的多体势函数利用分子动力学方法对Bi2Te3纳米薄膜沿着力学性能较差的c轴方向进行单轴拉伸模拟。拉伸之前对系统进行弛豫，考察了弛豫过程中系统能量、温度和初始应力的变化。根据拉伸过程中原子构型发现此方向的断裂是沿着晶体中结合力较弱的Te1-Te1层断开。由拉伸过程中的应力-应变和能量-应变变化曲线发现Bi2Te3薄膜沿c轴方向拉伸的破坏形式表现为明显的脆性断裂的特征。受温度的影响纳米薄膜的弹性常数、极限强度与破坏应变随温度升高而减小。

[1]Tang X F, Xie W J, Li H, et al. Preparation and thermoelectric transport properties of high-performance P-type Bi2Te3with layered nanostructure[J]. Applied Physics Letters, 2007, 90: 012102-012104.

[2]Xie W J, Tang X F, Yan Y G, et al. High thermoelectric performance BiSbTe alloy with unique low-dimensional structure[J]. Journal of Applied Physics, 2009, 105: 113713-113715.

[3]Walachova J, Zeipl R, Zelinka J, High room-temperature figure of merit of thin layers prepared by laser ablation from Bi2Te3target[J]. Applied Physics Letters, 2005, 87: 081902-081907.

[4]Miyazaki Y, Kajitani T. Preparation of Bi2Te3films by electrodeposition[J]. Journal of Crystal Growth, 2001, 229: 542-546.

[5]Kwon S D, Ju B K, Yoon S J, et al. Fabrication of bismuth telluride-based alloy thin film thermoelectric devices grown by metal organic chemical vapor deposition[J]. Journal of Electronic Materials, 2009, 38: 920-924.

[6]Yang X Y, Wu D. The melting behaviors of the Nb(1 1 0) nanofilm: a molecular dynamics study[J]. Applied Surface Science, 2010, 256: 3197-3203.

[7]Cao G X, Chen X. Size dependence and orientation dependence of elastic properties of Zno nanofilms[J]. International Journal of Solids and Structures, 2008, 45: 1730-1753.

[8]Huang B L, Kaviany M. Ab initio and molecular dynamics predictions for electron and phonon transport in bismuth telluride[J]. Physical Review B, 2008, 77: 125209-125223.

[9]Tong Y, Yi F J, Liu L S, et al. Molecular dynamics study on thermo-mechanical properties of bismuth telluride bulk[J]. Computational Materials Science, 2010, 48: 343-348.

[10]Tong Y, Yi F J, Liu L S, et al. Molecular dynamics study of mechanical properties of bismuth telluride nanofilm[J]. Physica B, 2010, 405: 3190-3194.

[11]Plimpton S J. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117: 1-19.

[12]Humphrey W, Dalke A, Schulten K. VMD-visual molecular dynamics[J]. Journal of Molecular Graphics and Modelling, 1996, 14: 33-38.

[13]Drabble J R, Goodman C H. X-ray spectroscopic investigation of bismuth telluride[J]. Journal of Physics and Chemistry of Solids, 1958, 5: 142-147.