共形天线阵元位置误差校正的辅助阵元法
2010-01-26侯青松王布宏
侯青松,郭 英,王布宏,唐 浔
(空军工程大学电讯工程学院,西安 710077)
共形天线阵元位置误差校正的辅助阵元法
侯青松,郭 英,王布宏,唐 浔
(空军工程大学电讯工程学院,西安 710077)
共形天线的安装和测量以及载体平台表面的变形和振动均会引起阵元位置误差,严重影响共形天线的测向性能。通过设置4个方位未知的精确校正的辅助阵元,实现了共形天线大尺度三维的阵元位置误差校正。给出了阵元位置误差条件下共形天线导向矢量的方位依赖的幅相误差等效表示模型;基于子空间原理得到等效的方位依赖的幅相误差估计,进而得到共形天线阵元的三维位置误差估计。该方法可以实现共形天线校正信源来波方位和阵元三维位置误差的联合但“去耦”估计。计算机仿真结果验证了共形天线阵元位置误差校正的辅助阵元法的有效性。
共形天线;阵列校正;位置误差校正;辅助阵元法
1 引 言
相对于传统的线阵和面阵,共形天线具有优良的空气动力学性能、更宽的波束扫描范围、更小的雷达散射截面积和更大的阵列天线孔径等优势。因此,共形天线一方面为改善民用电子产品的体积和外观提供了可行的技术解决方案,同时它提高了导弹、航空、航天和临近空间飞行器等的生存力和战斗力,成为各军事强国争相发展的核心军事技术之一[1]。
在共形天线实用化进程中,由于天线单元间相互的电磁耦合和阵元实际位置与标称位置存在误差,使得共形天线的阵列流形矢量与理想的阵列流形矢量不一致,严重影响了各种阵列信号处理算法的性能。对于共形天线互耦的分析通常都是采用电磁分析的方法来实现[1,2],但是互耦电磁计算值的精度还不理想,运算量大;文献[3]提出了共形天线互耦较正的辅助阵元法,将阵列的互耦校正转化为互耦系数的估计问题,为阵列的实时校正提供了可能。同样,由于天线阵制造、安装和维修等实际因素的影响,阵元位置误差不可避免地存在。阵元实际位置与标称位置间的偏差,严重影响了常规阵列测向算法的性能[4,5]。目前,国内外在解决这类问题中已进行了一系列的探索[6-9]。但是针对共形天线大尺度三维的阵元位置误差的校正问题尚未见报道,正是基于此,本文在文献[10]给出的共形天线流形矢量建模的基础上,通过设置精确校正的辅助阵元,对共形天线阵元三维位置误差进行校正。
2 共形天线阵元位置误差模型及其描述
假设具有任意几何结构的N元阵列,建立如图1所示的阵列坐标系,其中,θ为空间信源的俯仰角,φ为空间信源的方位角。其第i个阵元在(θ,φ)处的单元方向图为gi(θ,φ),它可以分解为两个正交的极化向量giθ和gi。文献[1]给出了共形天线在没有阵元位置误差条件下的阵列流形的数学模型,其空间信源的导向矢量a(θ,φ)可表示为


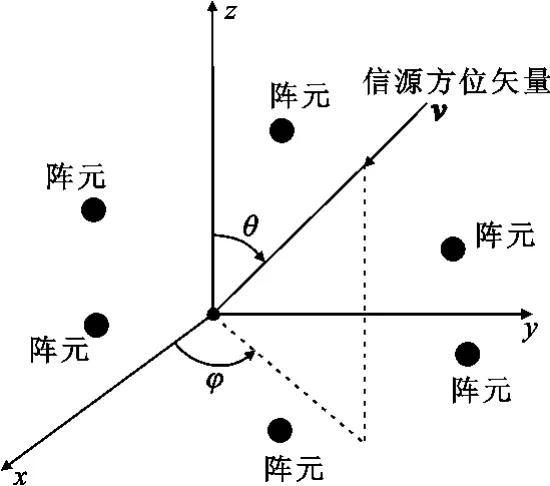
图1 三维阵列坐标系示意图Fig.1 Coordinate system of arbitrary 3D array antenna
3 共形天线阵元位置误差的辅助阵元校正法
文献[9]提出了一种方位依赖幅相误差校正的辅助阵元法,实现了多源情况下对信源方位及其阵元幅相误差的联合估计。由于共形天线阵元位置存在三维误差,需要3个方位未知的校正信源才能估计出阵元位置误差。由于辅助阵元法要求辅助阵元个数多于校正信源个数,因此需要引入4个精确校正(坐标已知或以它们为坐标参考)的辅助阵元。本节通过借鉴辅助阵元法的思想,通过设置4个精确校正的辅助阵元对校正信源的方位和由阵元位置误差引入的方位依赖的幅相误差进行联合估计。


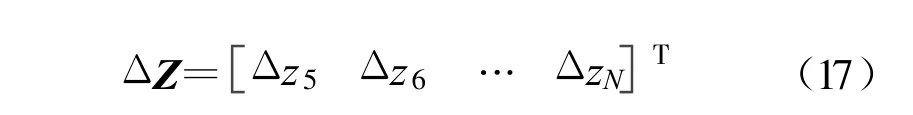
可见,采用辅助阵元法实现了共形天线校正信源来波方位和阵元位置误差估计的联合但“去耦”估计。需要说明的是,在对式(13)中的方位和俯仰角进行二维搜索时,可先进行粗搜索,大致确定校正信源来波方位范围,然后精搜索,获得校正信源来波方位更精确的估计,以减小运算量,提高搜索速度。
4 仿真实验

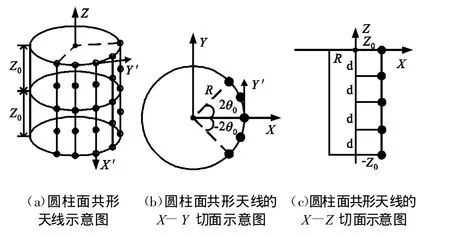
图2 圆柱面共形天线示意图Fig.2 Cylindrical array of 25 elements in simulation
天线单元采用微带贴片单元,单元方向图的两个分量可以如下表示[11]:
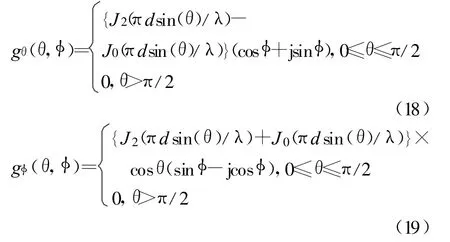
式中,J0为零阶第一类贝塞尔函数,J2为二阶第一类贝塞尔函数。
图3为式(13)在方位角和俯仰角均为(10°,60°)范围内的二维功率谱,通过搜索得到3个未知校正信源的方位和俯仰角估计。然后联合估计得到的方位俯仰角和对应的最小特征矢量,通过式(16)计算求得阵元三维位置误差估计值。
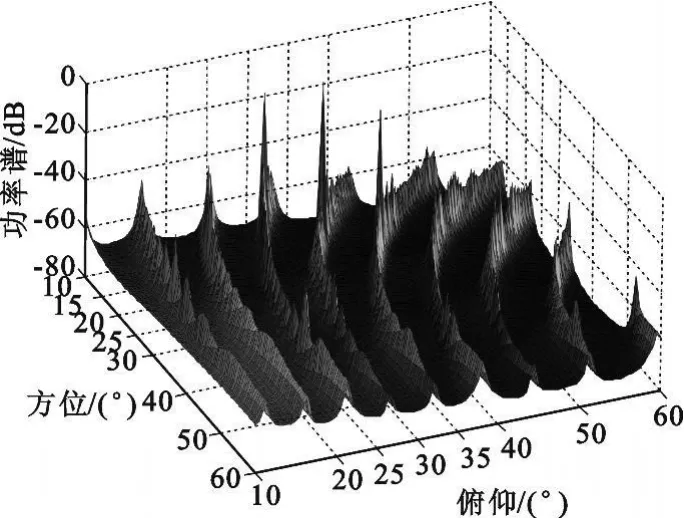
图3 校正信源DOA估计Fig.3 DOAs of the calibrating sources
图4给出了阵元理想位置、实际位置和估计位置,实验结果表明该方法实现了共形天线阵列的三维位置误差的自校正。
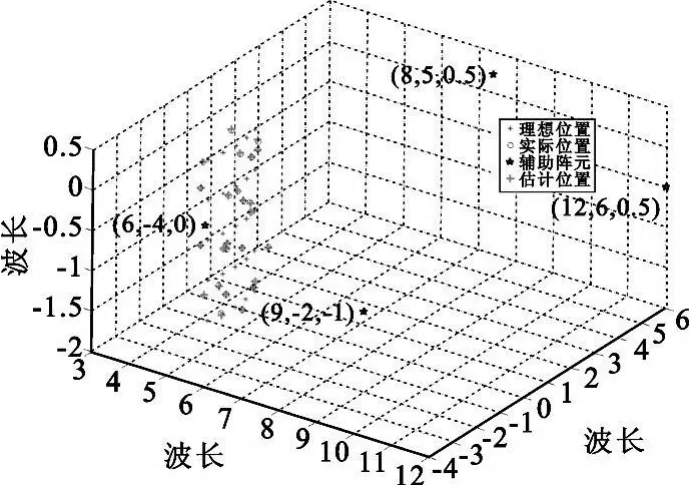
图4 理想、扰动和估计阵列形状Fig.4 Ideal,perturbed and estimated array shape
5 结 论
本文通过设置4个方位未知的精确校正的辅助阵元,实现了共形天线大尺度三维的阵元位置误差校正。该方法可以实现共形天线校正信源来波方位和阵元三维位置误差的联合但“去耦”估计,为共形天线的具体工程应用奠定相关理论基础。计算机仿真结果验证了共形天线阵元位置误差校正的辅助阵元法的有效性。需要说明的是,本文仅考虑共形天线阵元位置误差不具有时变性的情况。由于机载共形天线特有的严峻复杂的工作环境、飞行惯性(Inertial Forces)和空气动力负载(Aerodynamic Loads)的相互作用使得机载共形表面的变形(Deformations)和振动(Vibrations)具有时变性。针对这一问题,我们将在随后的论文中进行报道。
[1] Josefsson L,Persson P.Conformal Array Antenna Theory and Design[M].Wiley:IEEE,2006.
[2] Persson P,Josefsson L,Lanne M.Investigationof the Mutual Coupling Between apertures on Doubly Curved Convex Surfaces:Theory and Measurements[J].IEEE Transactions on Antennas and Propagation,2003,51(4):682-692.
[3] 王布宏,侯青松,郭英,等.共形阵列天线互藕校正的辅助阵元法[J].电子学报,2009,36(6):1283-1288.
WANG Bu-hong,HOU Qing-song,GUO Ying,et al.Mutual Coupling Calibration for ConformalArray Antenna with Instrumental Sensors[J].Acta Electronica Sinica,2009,36(6):1283-1288.(in Chinese)
[4] 刘洪盛,肖先赐.线阵阵元位置误差造成的测向误差估算[J].电波科学学报,2006,21(5):717-721.
LIU Hong-sheng,XIAO Xian-ci.Estimation of direction finding errors caused by sensor positions errors of linear array[J].Chinese Journal of Radio Science,2006,21(5):717-721.(in Chinese)
[5] 刘洪盛,肖先赐.面阵测向性能相对于阵元位置误差敏感性研究[J].电波科学学报,2008,23(1):90-94.
LIU Hong-sheng,XIAO Xian-ci.Sensitivity analysis of DF performance of p lanar array with respect to array uncertainties[J].Chinese Journal of Radio Science,2008,23(1):90-94.(in Chinese)
[6] Weiss A J,Fried lander B.Array shape calibration using sources in unknown locations-A maximum likelihood approach[J].IEEE T ransactions on ASSP,1989,37(12):1958-1966.
[7] Weiss A J,Friedlander B.Array shape calibration using eigenstructure methods[J].Signal Processing,1991,22(3):251-258.
[8] 章宏,陈荆花,周希朗.阵列天线阵元位置误差、通道不一致和互耦的校正[J].上海交通大学学报,2002,36(9):1284-1290.
ZHANG Hong,CHEN Jing-hua,ZHOU Xi-lang.Calibration Technique for Sensor Position Uncertainty,ChannelMismatch andMutual Coupling of Sensor-Array[J].Journal of Shanghai Jiaotong University,2002,36(9):1284-1290.(in Chinese)
[9] 王布宏,王永良,陈辉,等.方位依赖阵元幅相误差校正的辅助阵元法[J].中国科学(E辑),2004,34(8):906-918.
WANG Bu-hong,WANG Yong-liang,CHEN Hui,et al.Array calibration of angularly dependent gain and phase uncertaintieswith carry-on instrumental sensors[J].Science in China Ser.E Information Sciences,2004,34(8):906-918.
[10] 王布宏,郭英,王永良,等.共形天线阵列流形的建模方法[J].电子学报,2009,37(3):481-484.
WANG Bu-hong,W ANG Yong-liang,GUO Ying,et al.Array manifold modeling for conformal array antenna[J].Acta Electronica Sinica,2009,37(3):481-484.(in Chinese)
[11] VASKELAINEN L I.Iterative least-squares synthesis methods for conformal array antennas with op timized polarization and frequency properties[J].IEEE Transactions on Antennas Propagation,1997,45(7):1179-1185.
Array Shape Calibration for Conformal Antenna w ith Instrumental Sensors
HOU Qing-song,GUO Ying,WANG Bu-hong,TANGXun
(The Telecommunication Engineering Institute,Air Force Engineering University,Xi′an 710077,China)
Both of the installation and measurement of conformal antenna cause position errors of its elements.And its supporting structure is also subjected to deformation and vibration.As a consequence,the positions of its elements change.Its performance of direction finding is seriously affected.In this paper array shape calibration algorithm for conformal array antenna is developed by using four accurately calibrated instrumental sensors with unknown DOAs.The array steering vector in the presence of position errors is expressed as angularly dependent gain and phase uncertainties.The angularly dependent gain and phase uncertainties are estimated based on subspace direction finding technique.And then the 3D position errors of the elements are calculated sequentially.The proposed calibration method can estimate the DOAs of the auxiliary calibrating sources and the position errors jointly.Computer simulation demonstrates that the proposed algorithm is effective.
conformal antenna;array calibration;array shape calibration;instrumental sensors method
The National Natural Science Foundation of China(No.60601016);The Natural Science Basic Research Plan in Shaanxi Province(No.2010JQ8003);Graduate StudentFoundation of Telecommunication Engineering Institute,Air Force Engineering University(No.200707)
TN911
A
10.3969/j.issn.1001-893x.2010.11.005
1001-893X(2010)11-0021-05
2010-07-16;
2010-08-30
国家自然科学基金资助项目(60601016);陕西省自然科学基础研究计划项目(2010JQ8003);空军工程大学电讯工程学院研究生论文创新基金项目(200707)
侯青松(1981-),男,四川营山人,空军工程大学电讯工程学院博士研究生,主要研究方向为阵列信号处理、阵列校正等;
HOU Qing-song was born in Yingshan,Sichuan Province,in 1981.He is currently working toward the Ph.D.degree at the Telecommunication Engineering Institute of Air Force Engineering University.His research interests include array signal processing and array calibration.
Email:cnhqs@163.com
郭 英(1961-),女,山西临汾人,空军工程大学电讯工程学院教授、博士生导师,主要研究方向为通信信号处理、自适应信号处理等;
GUO Ying was born in Linfen,Shanxi province,in 1961.She is now a p rofessor and also the Ph.D.supervisor.Her research interests include signal processing for communications and adaptive signal processing.
Email:Guoying-dsp@sina.com
王布宏(1975-),男,山西太原人,博士(后),副教授,主要研究方向为阵列信号处理、阵列校正等。
WANG Bu-hong was born in Taiyuan,Shanxi Province,in 1975.From 2003 to 2005,he was a PostdoctoralFellow in the Postdoctoral Technical Innovation Centre,Nan jing Research Institute of Electronics Technology.He is now an associate professor.His research interests include array signal processing and array calibration.
Email:wbucx@yahoo.com.cn
