基于PSWF的非正弦时域正交频分调制方法

刘锡国,张 磊,舒根春,刘传辉

（海军航空工程学院,山东烟台 264001）

非正弦时域正交调制在大相对带宽下存在的主要问题是脉冲产生的计算量大、复杂度高、系统实现困难、抗多径性能差、不利于对调制信号进行均衡和比特加载等。在大相对带宽系统下的非正弦时域正交调制存在大相对带宽与子带数目的矛盾:为了提高系统的抗多径性能、便于进行均衡和比特加载,希望系统内各脉冲具有小相对带宽的特性;而为了降低脉冲组设计的复杂度,提高系统的可实现性,希望系统具有最少的并行脉冲路数。若要求系统具有较好的抗多径性能,并且便于进行均衡和比特加载,则需要将系统工作频段划分为很多个子频段,在每个子频段内求解脉冲波形,并对所有脉冲进行施密特正交化,这样会导致系统实现复杂度过高,并且施密特正交化会改变原脉冲波形,破坏原有脉冲的频谱特性,造成调制信号相位跳变,影响系统性能。

基于PSWF的非正弦时域正交频分调制方法

刘锡国,张 磊,舒根春,刘传辉

（海军航空工程学院,山东烟台 264001）

针对现有非正弦时域正交调制方法应用于大相对带宽系统中存在脉冲组设计复杂度高、实现困难、不利于对调制信号进行均衡和比特加载的问题,提出一种改进的非正弦时域正交频分调制方法。把频分复用的思想用于该调制方法,将工作频段分为多个相邻的子频段,在每个子频段内分别进行非正弦时域正交调制,利用频分特性避免了在不同频段内进行施密特正交化,降低了调制器的复杂度并且有利于信道均衡和比特加载。仿真结果表明,相同条件下,改进的调制方法与原有方法的误码性能几乎相同。该调制方法复杂度低、易于实现,有利于进行均衡和比特加载,抗多径性能强,更适用于大相对带宽有线或无线通信系统。

大相对带宽系统;非正弦时域正交调制;椭圆球面波函数;频分复用;正交化

1 引 言

非正弦时域正交调制（Nonsinusoidal Orthogonal Modulation in Time Domain,NOM）[1]是一种新的高效调制方法,它不采用正余弦载波,而是采用频谱集中度最佳的基于椭圆球面波函数（Prolate Spheroidal Wave Function,PSWF）[2-4]时域正交脉冲组多路并行传输信息,是一种脉冲并行传输体制,其调制信号频谱可控、能量聚集性好,可不经滤波直接用于发射。该调制方法通过频谱混叠减小信号占用的频谱带宽,系统的频带利用率可快速接近奈奎斯特极限,其理论性能高于OFDM（Orthogonal Frequency Division Multiplexing）[5-7],可以用于有线或无线通信,是一种应用前景广阔的调制方式。

但是,非正弦时域正交调制方法首先需要根据系统的频域特性求解时域波形,再通过施密特正交化构建时域正交脉冲组。在宽带系统中,考虑到均衡、比特加载和抗多径性能[8-12]的要求,脉冲组内各脉冲需要具有小相对带宽的特点,因此需要划分较多子频带,导致脉冲组内的脉冲数目过多,施密特正交化后脉冲波形和相位变化较大,多路叠加后调制信号频谱特性会发生变化,影响系统的性能。

针对该问题,本文提出一种改进的非正弦时域正交频分调制方法,在宽带系统的工作频段上,将系统频段分为多个带宽相同的较窄的子频段,在子频段上分频段构建子脉冲组,用于加载信息。由于PSWF的能量聚集性高,在各子频段上的分组调制信号频谱能量几乎完全集中在子频段内,相邻子频段满足频分复用（Frequency Division Multiplexing,FDM）的条件,因此可通过多种方法[13,14]进行子频段分离和解调。采用分组调制的方法可提高系统的抗多径性能,降低系统复杂度,同时分组调制的结构更加有利于均衡和比特加载。

2 非正弦时域正交调制

非正弦时域正交调制采用基于椭圆球面波函数的时域正交脉冲组加载信息,调制信号的频谱特性由正交脉冲组决定,系统的传输速率和误码性能也由脉冲组的正交特性决定。因此,时域正交脉冲组的特性直接影响到整个系统的性能,正交脉冲组设计是非正弦时域正交调制通信系统的核心和关键。非正弦时域正交调制是本文提出方法的基础,因此这里首先详细介绍其基本原理。

2.1 时域正交脉冲组设计

非正弦时域正交调制系统要求正交脉冲组必须具有高能量聚集特性和时域正交特性,而椭圆球面波函数（PSWF）是已知的能量聚集性最高的非正弦函数,并且它具有双正交性和完备性[13],因此可以利用其优良特性设计时域正交脉冲组。由于PSWF没有解析解,一般采用数值求解算法[13,14],并且频段不同的PSWF不一定具有时域正交特性,因此需要进行施密特正交化。基于PSWF的正交脉冲组设计构建需要经过频段划分、波形求解、施密特正交化等步骤完成。

假设系统的工作频段为B=fH-fL,其中B为系统总带宽。将该频段等分为K个子频段,其中第k个子频段为:Bk=fk,H-fk,L,fk,L和fk,H表示第k个子频段的频率下限和频率上限,各子频段带宽相同均为B0且相互间部分交叠,频段划分示意图如图1所示。

图1 频段划分示意图Fig.1 The diagram of band division

在第k个子频段上,根据PSWF脉冲的参数构建特性方程:

2.2 调制解调模型

非正弦时域正交调制解调系统模型如图2所示。

图2 非正弦时域正交调制解调模型Fig.2 The modulation/demodulation model of NOM

由图2所示的调制模型可知,非正弦时域正交调制信号在一个码元周期内可表示为

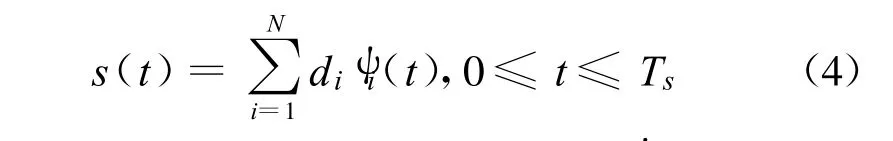
式中,di为第i路待传的二进制数据,ψi（t）为时域正交脉冲组中第i个脉冲,Ts为码元持续时间,N为并行传输路数。可见,高速串行数据流经串并转换变为低速并行数据流,分别与对应支路的正交脉冲进行调制,最后经时域叠加变为一路合成信号。

由图2所示的解调模型可知,接收信号经带通滤波后分别送入相关解调器中进行解调,根据脉冲组的时域正交特性,接收信号r（t）分别与第i路本地模板脉冲ψi（t）进行积分运算,接收信号中,只有ψi（t）携带的信息di能够解调出来,其余支路与ψi（t）积分的结果均为零,从而达到分离和解调各支路信号的目的。在理想情况下,第i路相关器的输出可表示为

2.3 大相对带宽下的问题

非正弦时域正交调制在大相对带宽下存在的主要问题是脉冲产生的计算量大、复杂度高、系统实现困难、抗多径性能差、不利于对调制信号进行均衡和比特加载等。在大相对带宽系统下的非正弦时域正交调制存在大相对带宽与子带数目的矛盾:为了提高系统的抗多径性能、便于进行均衡和比特加载,希望系统内各脉冲具有小相对带宽的特性;而为了降低脉冲组设计的复杂度,提高系统的可实现性,希望系统具有最少的并行脉冲路数。若要求系统具有较好的抗多径性能,并且便于进行均衡和比特加载,则需要将系统工作频段划分为很多个子频段,在每个子频段内求解脉冲波形,并对所有脉冲进行施密特正交化,这样会导致系统实现复杂度过高,并且施密特正交化会改变原脉冲波形,破坏原有脉冲的频谱特性,造成调制信号相位跳变,影响系统性能。

3 改进的频分调制方法

针对上述问题,本文提出一种基于频分复用的非正弦时域正交频分调制方法。主要思想是:将系统的工作频段平均分为多个子频带,各子频带紧密相邻,没有保护带宽,在每个子频段内利用时域正交脉冲组构建方法构建子脉冲组,并利用各子脉冲组分别调制信号,调制经多路叠加,合成一路信号并行传输。解调时,接收信号经带通滤波器后直接采用分组相关解调方式进行解调,最后将各组解调信号还原为单路信号。在该分组调制方法中,非正弦时域正交子脉冲组的构建是系统的关键。下面首先对正交子脉冲组进行分析。

3.1 分组正交子脉冲组设计

考虑系统要求的频带利用率、均衡的难易度、信道特性等因素,结合系统实现的复杂度和参与施密特正交化的脉冲个数确定子频段数L,将工作频段B=fH-fL划分为L个相邻的子频段,每个子频段的带宽在每一个频段内,根据系统要求的频带利用率,确定PSWF的时间带宽积C和子频带个数M,并将子频段划分为M个相互交叠的子频带,相邻子频带交叠度为η,每个子频带带宽为B0,B0满足:子频段及子频段内的子频带划分方案如图3所示。

图3 频分调制频段划分示意图Fig.3 The new band division diagram

按照上述频段划分方法,采用文献[14]的方法在各子频段内分别设计求解子脉冲组,可以得到L组子脉冲组。

3.2 分组调制解调方法

利用上述子脉冲组即可完成分组调制和解调。调制和解调示意图如图4所示。

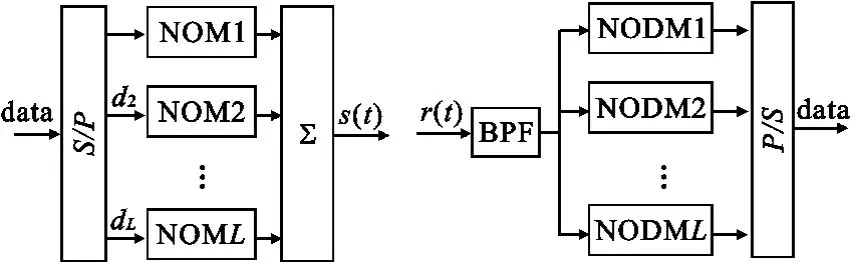
图4 分组调制解调模型Fig.4 The modulation/demodu lationmodel of NOBD M

由图可知,在发射端,信源信号经串并转换变为与各分组子脉冲相对应的多路并行子信源,采用各分组子脉冲对相应的子信源进行非正弦时域正交调制,最后将各路调制信号经时域叠加合成为一路信号,经信道进行传输。在接收端,接收信号经多个对应于各子频段的带通滤波器滤波,分组进行相关解调,得到多路解调信号,最后经并串转换变为一路解调信号输出。

4 性能仿真及分析

本节分析改进的非正弦时域正交频分调制方法的频带利用率及功率谱特性,通过蒙特卡罗仿真研究了该方法在理想同步条件下、AWGN信道下的误码性能。仿真参数设置如下:假设系统工作在超宽带频段,fL=3.82 GHz,fH=7.64GHz,带宽B=3.82 GHz。根据本文提出的方法,将系统工作频段分为5个子频段,每个子频段带宽B′=0.764 GHz。取PSWF脉冲的时间带宽积C=2.2π,频谱交叠度ρ=55%,分别在各个子频段内设计子脉冲组。

4.1 频带利用率

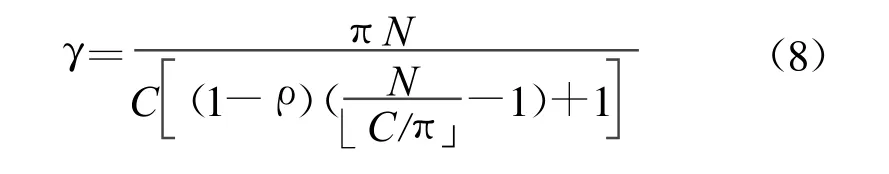
非正弦时域正交调制系统的频带利用率可表示为式中,N为传输路数。它具有比OFDM更高的频带利用率,其频带利用率随着并行传输路数迅速趋近于2 bit/s·Hz-1的奈奎斯特极限。改进的分组调制方法中,每一个子频段上采用非正弦时域正交调制,其频带利用率也满足式（8）,由于各子频段间没有间隔,系统总的频带利用率与每一个子频段上频带利用率相同。因此改进的分组调制系统的总的频带利用率可表示为

式中,L表示系统划分的子频段数。

当C=2.2π、ρ=55%,每个子频段内取C/π」=2个脉冲,划分的子频段L取不同值时,改进的分组调制系统的频带利用率与总的并行传输路数N的关系曲线如图5所示。

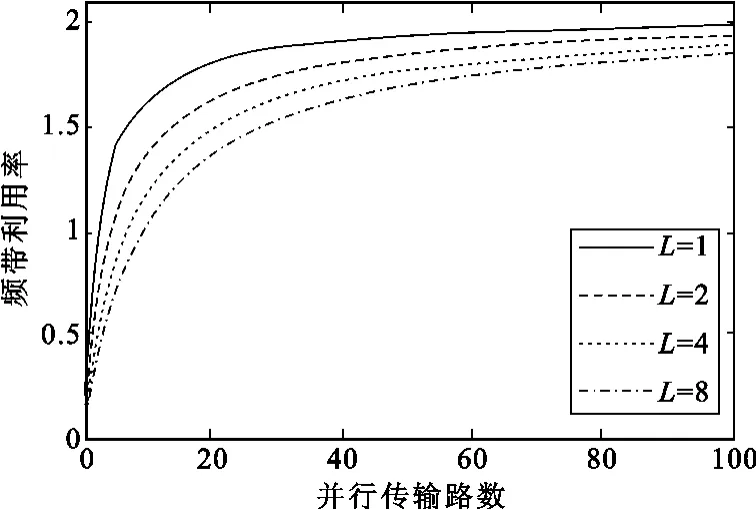
图5 并行传输路数与系统的频带利用率曲线Fig.5 The data rate-to-bandwidth ratio versus number of parallel channels

由图可见,当划分的子频段增加时,系统的频带利用率随着总的并行路数N增大的速率有一定的降低,但是其趋近速度仍然较快,因此仍可以以较少的并行路数迅速提高频带利用率。

4.2 功率谱特性

非正弦时域正交调制是一种脉冲通信体制,其功率谱特性与脉冲的频谱关系密切。在上述仿真条件下,采用改进的非正弦时域正交频分调制方法仿真得到了调制信号的功率谱,如图6所示。

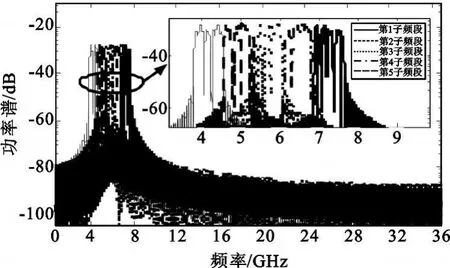
图6 频分调制信号功率谱Fig.6 The power spectrum of NOBDM signal

由图可见,调制信号的功率谱滚降特性非常好,旁瓣达到-40 dB以下,并且各子频段频谱相邻、互不交叠,保证了不同子频段内脉冲分离的条件。

4.3 误码特性

在上述仿真条件下,采用改进的非正弦时域正交频分调制方法对二进制随机信源进行调制,经AWGN信号后进行解调。假定理想同步,采用10万个码元进行仿真,分析其在AWGN信道下的误码性能。为了便于比较,本文还给出了相同条件下非正弦时域正交调制系统的误码特性理论和仿真曲线。误码特性曲线如图7所示。

图7 误码特性曲线Fig.7 The curve of BER performance

由图7可知,改进的频分调制方法的误码性能与原非正弦时域正交调制方法几乎相同,并且与理论值吻合较好。需要指出的是,该仿真是在各子频段旁瓣小于-40 dB的情况下完成的,因此各子频段间脉冲几乎没有相互干扰。实际工程中,由于器件性能和脉冲发生器精度的影响,可能无法生成能量聚集性这样好的脉冲频谱,各子频段间会产生一定的干扰,影响系统性能。

5 结 论

结合PSWF的高能量聚集特性,本文将频分复用的思想应用于非正弦波通信中,提出了一种基于椭圆球面波函数的非正弦时域正交频分调制方法,

降低了系统脉冲组设计的复杂度,并且更有利于进行均衡、比特加载和抗多径性能的提高。在超宽带频段下,分析了系统的频带利用率和功率谱,理论分析并采用Monte Carlo仿真验证系统的误码性能并与原时域正交调制进行了比较。分析和仿真结果表明,本文提出的改进方法与原有的调制方法性能相当,更适用于大相对宽带有线或无线通信系统。

[1] 王红星,赵志勇,刘锡国,等.非正弦时域正交调制方法:中国,CN101409697A[P].2009.

WANG Hong-xing,ZHAO Zhi-yong,LIU Xi-guo,et al.The method of nonsinusoidal orthogonal modulation in time domain:China,CN101409697A[P].2009.（in Chinese）

[2] Lindquist M A,Zhang C,Glover G,et al.A generalization of the two-dimensional prolate spheroidal wave function method for nonrectilinear MRI data acquisition methods[J].IEEE Transactions on Image Processing,2006,15（9）:2792-2804.

[3] Wei L,Kennedy R A,Lamahewa T A.Further results on signal concentration in time-frequency[C]//Proceedings of 2010 IEEE International Conference on Acoustics Speech and Signal Processing.Dallas,TX,USA:IEEE,2010:4082-4085.

[4] Lin Z,M cCallum R W,Wang H.Computation and performance of the prolate-spheroidal wave function window in spectral estimation[C]//Proceedings of 1996 International Conference Acoustics,Speech,and Signal Processing.Atlanta,GA:IEEE,1996:2976-2978.

[5] Keonkook Lee,Youngok Kim,Nam jeong Lee,et al.Adaptive switching between space-time and space-frequency block coded OFDM systems[C]//Proceedings of MILCOM 2008.San Diego,CA:IEEE,2008:1-5.

[6] Char-Dir Chung.Spectral precoding for constant-envelope OFDM[J].IEEE Transactions on Communications,2010,58（2）:555-567.

[7] Ryu H.System design and analysis of MIMO SFBC CIOFDM system against the nonlinear distortion and narrowband interference[J].IEEE Transactions on Consumer Electronics,2008,54（2）:368-375.

[8] Marelli D,Minyue F.Subband methods for OFDM equalization[C]//Proceedings of 2003 International Conference on Communications.Anchorage,Alaska,USA:IEEE,2003:2350-2354.

[9] Wang D,Cao Y,Zheng L.Efficient Two-Stage Discrete Bit Loading Algorithms for OFDM Systems[J].IEEE Transactions on Vehicular Technology,2010,59（7）:3407-3416.

[10] Shin C,Park H,Kang J,et al.A per-stream coded bit loading algorithm for MIMO BIC-OFDM systems[C]//Proceedings of 2010 International ITG Workshop on Smart Antennas.Bremen:IEEE,2010:240-243.

[11] Chen S,Xu W,Wang L,et al.Performance of FM-DCSK UWB with timing error[C]//Proceedings of the 9th International Symposium on Communications and Information Technology.Icheon:IEEE,2009:1152-1156.

[12] Xu H,Zhu Y,Wang G.On the anti-multipath performance of UWB signals in indoor environments[C]//Proceedings of the 4th International Conference on Microwave and Millimeter Wave Technology.Beijing:IEEE,2004:163-166.

[13] Xiao H,Rokhlin V,Yarvin N.Prolate spheroidal wave functions,quadrature and interpolation[J].Inverse Problems,2001,17（4）:805-838.

[14] Parr B,Cho B,Wallace K.A novel ultra-wideband pulse design algorithm[J].IEEE Communication Letters,2003,7（5）:219-221.

A Novel Nonsinusoidal Orthogonal Band Division M odulation（NOBDM）M ethod Based on PSWF

LIU Xi-guo,ZHANG Lei,SHU Gen-chun,LIU Chuan-hui
（Naval Aeronautical and Astronautical University,Yantai 264001,China）

In allusion to the problem that the design of pulse sets is complex,difficult to be realized and be unfavourable for the equalization and bit loading when existing nonsinusoidal orthogonal modulation in time domain（NOM）method is applied in large broadband systems,a novel nonsinusoidal orthogonal band division modulation method（NOBDM）is proposed.The idea of frequency division multiplexing（FDM）is used in NOM method.The frequency band of the system is divided into a lot of shoulder-to-shoulder subbands and the NOM is used in each subband.Due to the best energy concentration character of the Prolate Spheroidal Wave Function（PSWF）,the modulated signals of different bands are not interfered each other.The novel method not only has the advantages for equalization and bit loading but also reduces the complexity of orthogonal pulse sets design and implementation.The resultsof the Monte Carlo simulation show that the proposed method has approximate the same BERperformance as the old ways.The scheme is suitable for the wire or wireless broadband communication systems.

broadband communication system;nonsinusoidal orthogonal modulation in time domain;PSWF;frequency division multiplexing（FDM）;orthogonality

TN911.3

A

10.3969/j.issn.1001-893x.2010.11.004

1001-893X（2010）11-0015-06

2010-07-16;

2010-09-02

刘锡国（1981-）,男,山东烟台人,2007年获工学硕士学位,现为博士研究生,主要研究方向是现代通信新技术、非正弦波通信等;

LIU Xi-guo was born in Yantai,Shandong Province,in 1981.He

theM.S.degree in 2007.He is currently working toward the Ph.D.degree.His research interests include modern communication technology and non-sinusoidal communications.

Email:lxg1023@163.com

张 磊（1979-）,男,安徽合肥人,2005年获工学硕士学位,现为博士研究生,主要研究方向为现代通信新技术、超宽带通信、非正弦波通信等;

ZHANG Lei was born in Hefei,Anhui Province,in 1979.He received the M.S.degree in 2005.He is currently working toward the Ph.D.degree.His research interestsinclude modern communication technology,UWB communications and non-sinusoidal communications.

Email:win-romance@163.com

舒根春（1970-）,男,浙江金华人,2006年获工学硕士学位,现为博士研究生,主要研究方向为现代通信系统、数字信号处理、非正弦波通信等;

SHU Gen-chun was born in Jinhua,Zhejiang Province,in 1970.He received the M.S.degree in2006.He is currently working toward the Ph.D.degree.His research interests include modern communication technology,signal processing and non-sinusoidal communications.

Email:sgc31@sohu.com

刘传辉（1984-）,男,山东济宁人,2008年获工学硕士学位,现为博士研究生,主要研究方向为现代通信新技术、非正弦波通信等。

LIU Chuan-hui was born in Jining,Shandong Province,in 1984.He received the M.S.degree in2008.He is currently working toward the Ph.D.degree.H is research interests include modern communication technology and non-sinusoidal communications.

Email:lchgfy@163.com