测量动光栅瞬时速度的有效方法
2010-01-26陈长鹏汪礼胜
陈长鹏,汪礼胜
(武汉理工大学物理科学与技术系,湖北武汉430070)
1 实验原理
当频率为ω0的激光束垂直入射到以速度 v运动的光栅时,从光栅出射的光束各衍射级的频率可以合写成[1]

式(1)中,n是衍射级次,nωd是多普勒频移.ωd与光栅常量 d及速度v的关系为[1]

因此,如果能测出多普勒频移 nωd,就可以确定运动光栅的速度v.假如光栅是固定在一运动的物体上,通过测量衍射光的瞬时多普勒频移就可以定出物体的瞬时运动速度.
2 双光栅的衍射光和光电流
要测量瞬时多普勒频移,首先要分析双光栅的衍射光和相应的光电流.图1是激光束依次通过动光栅、静光栅后的衍射光束分布图,其中光束1和光束2是相互平行的.由于 He-Ne激光器发出的是有一定宽度的光束(束腰直径约为1.2 mm),所以只要两光栅的距离比较小,则两光束在空间会有重叠的部分,故两光束能叠加从而形成光拍[1].光拍信号进入硅光电池后,输出的光电流为[1]

其中ξ为硅光电池的光电转换系数,E10和 E20分别是两光束光场的振幅,φ1和φ2依次是两光束光电场的初相位,I0是光电流的直流部分.硅光电池输出的光电流是很小的,为了便于处理应进行放大.
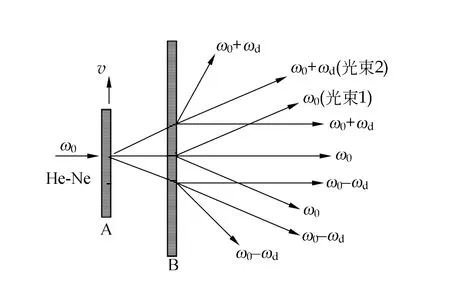
图1 ±1级衍射光波的多普勒频移
3 微电流放大器
用硅光电池作检测元件时,是把它作为电流源来使用的(如图2的虚线框中所示).但式(3)所表示的光电流is通常很小,必须利用运算放大器进行放大.图2是 T形网络电路组成的微电流放大和 I/V转换电路,在理想的情况下有[2]

将 u=-isR1代入_(4)式可求得输出电压为

把式(3)代入式(5)可得
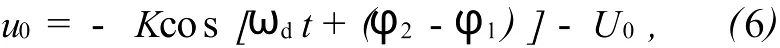
式中

由式(2)和式(6)可以看出:要测出瞬时速度,需要解决瞬时频率ωd的测量问题.

图2 微电流放大电路
4 瞬时频率和速度的测量
目前,瞬时频率的估计一般采用3种方法来解决,分别是:相位差分法、相位建模法和时频分布法[3].使用这3种方法来处理变频信号,首先是进行数据的采集,然后再送到微机系统用专门的应用软件进行处理得出瞬时频率值.由于这些估计瞬时频率的方法依赖特定的应用软件,故缺乏实时性.
在式(6)中,K是不变的常量,U0是信号的直流部分.因此,可采用相应的运算电路把式(6)转化为余弦函数的形式[2],即

式(7)中φ=ωdt+(φ2-φ1).余弦函数cosφ的幂级数展开式是
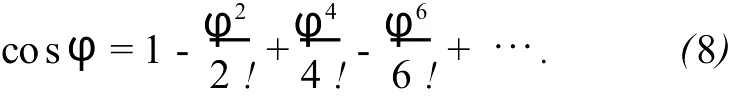
忽略8次幂以上的高次项,用图3所示的电路完成幂级数前4项的运算.
在图3中,幂级数运算电路由4个乘法器和3个运算放大器组成.容易得到幂级数运算电路的最终输出是
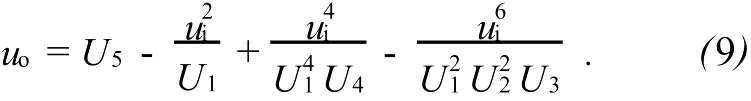
因此,当 U5=1 V,U1=2 V,U41U4=4!V,U21U22U3=6!V时,该电路能完成余弦函数的近似计算,也就是

图3 幂级数运算电路

为了解出瞬时频率,需要用到反余弦函数电路.图4是反函数运算电路,其中N4和N5是2个运算放大器,标有cos uo1的方框代表的是图3所示的幂级数运算电路.幂级数运算电路的输入端连至A点,输出端与运算放大器N5的负极性输入端相连,也就是将原函数运算电路接入反馈回路以达成实现反函数运算的目的.

图4 反余弦函数运算电路
对于理想的运算放大器,有

根据图4及前面的讨论,易知

由式(13)和式(14),可得到

因此,该电路实现了对输入信号 u1反余弦函数的运算.
由式(7)和式(13)可以看出:uo1对时间t的导数就是瞬时频率.这一任务由图5中的微分电路来完成.
在图5中,微分电路的输出是

而 uo1≈arccos u1,u1=cosφ,所以

由式(15)可以得到瞬时频率为

根据式(2)和式(16),瞬时速度为


图5 微分和计算电路
微分电路的输出接到单片机系统的A/D转换上.在编程求瞬时频率和瞬时速度时,先把R0C0和的值存放在1个通用寄存器上.A/D转换的结果除以 R0C0的值就是瞬时角频率,瞬时角频率除以就是动光栅的瞬时速度.经D/A转换后,由数码管显示实时频率和速度的瞬时值.这一测量系统,可用于物体运动范围限制在很小长度内的微振动速度的监测.
5 微振动速度的测量
图6是微振动速度测量系统的原理图.音叉在换能器的作用下做微振动,动光栅粘贴在音叉上.激光束通过动光栅、静光栅衍射,光电池对准光束1和光束2的方向(如图1所示);光电池输出的光电流通过微电流放大器,转换成电压(uo)输出;经过整形电路,把 uo转换成标准的余弦信号的输出;然后,经过反余弦函数运算电路、微分电路后,得到瞬时频率;最后,经过单片机的计算求出瞬时速度的值.
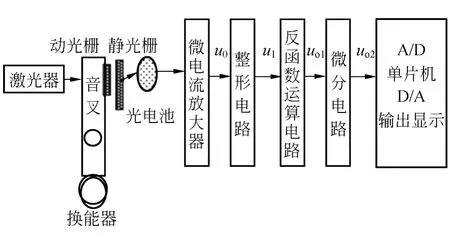
图6 微振动速度测量系统
表1是实测数据.其中,换能器的激振频率为50 Hz,激光打在动光栅的点距音叉的自由端0.03 m,动光栅的振幅为2 mm.

表1 微振动速度实测数据
上面这组数据是取自20 m s内的测量结果,也就是1个音叉振动周期内的数据.不难看出:上面数据的变化周期是10 m s,这是由于没有辨向电路导致的结果.
在1/4周期(5 m s)内,同等条件下,对动光栅进行动力学分析再结合数值计算,并且忽略动光栅的质量,得到的动光栅瞬时速度的理论值如表2所示.

表2 1/4周期内动光栅瞬时速度的理论值 m/s
把实测的数据和理论值进行对比,不难发现除了速度为0的3个数据的对偏差超过5%以外,其余的各个数据的相对偏差都未超过5%.之所以在速度为0的附近偏差较大,是因为采用了微分电路,速度为0对应频率为0.其余各组数据的偏差,主要是用级数来近似地代替余弦函数所导致.
6 结束语
虽然在速度为0的附近测量数据的偏差较大,但是其余的各个数据相对偏差都未超过5%,说明该方法是测量微运动瞬时速度的有效方法.怎样解决速度为0的附近测量数据的误差较大,这是一个值得探讨和有待解决的问题.
[1] 龙作友,戴亚文,杨应平,等.大学物理实验[M].武汉:武汉理工大学出版社,2008.
[2] 张国雄.测控电路[M].北京:机械工业出版社,2001:144-165.
[3] 陈水波.利用双光栅的多普勒频移测速度[J].物理实验,2007,27(7):6-9.
[4] 李正正,蔡虹,洪小刚,等.双光束激光多普勒测速系统[J].物理实验,2005,25(3):44-46.
[5] 冯松立,陈高平.瞬时频率估计的相位建模法及Matlab的实现[J].中国测试技术,2003,29(3)38,41.
