探研投币试验中的几种概率情形
2010-01-25徐瑞标
通化师范学院学报 2010年10期
徐瑞标
(武夷学院 教育科学系,福建 武夷山354300)
1 预备知识

设x>0和y都是整数,从原点到点(x,y)的路径{X1,…,Xn}就是一条折线,其顶点的横坐标为1,2,…,x,其顶点的纵坐标X1,X2,…,Xx满足Xi-Xi-1=ξi=±1(i=1,2,…,x),而且Xx=y.如果ξi中有m个正的n个负的,则x=m+n,y=m-n.反之,如果能用一条路径把(x,y)与原点联结起来,那么x,y必是形如x=m+n,y=m-n的数.这时,从x=

若终点(x,y)事先不固定,那么从原点到(n,y)(纵坐标y任意)的路径数便是前面所提到的2n条,这2n条路径可以解释为连续投一个均匀的硬币n次所得到的2n个可能结果,因此,序列{X1,X2,…,Xn}代表正面超过反面的累积次数.
2 主要定理及其证明
现在我们利用上述随机徘徊的有关知识投币试验中几种情形的概率来做讨论.
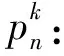

定理2 在一个n次投币试验中,出现正面次数多于出现反面次数的概率pn.
证明 当n=2k时,出现正面次数比反面次数多的次数只能为2,4,6,…,2k.由定理1可知,出现正面次数多于出现反面次数的概率
当n=2k+1时,出现正面次数比出现反面次数多的次数只能为1,3,5,…,2k+1.
由定理1可知:




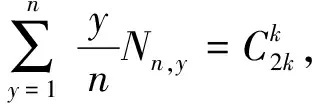

证明 此投币试验可视为满足条件X1≥0,

图1 路径示意图
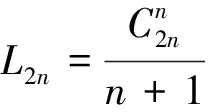
参考文献:
[1]钱敏平,龚光鲁.随机过程论[M].北京:北京大学出版社,1997.
[2]W.费勒.概率论及其应用(上)[M].胡迪鹤,等译.北京:科学出版社,1979.
