两种快速星像匹配算法的比较

任俊杰,彭青玉,3

(1.暨南大学计算机科学系，广州 510632；2.广东省高等学校光学信息与传感技术重点实验室，广州 510632;3.中国科学院光学天文联合开放实验室昆明基地，昆明 650011)

在现代天文观测中，大多使用CCD探测器来成像观测。为了快速提取每一幅CCD图像中观测对象的物理信息(如位置、光度等)，人们开发了多种自动处理软件。例如DAOPHOT[1]，DoPHOT[2]，SExtractor[3]等。为了方便资料的归算和处理，常常需要将图像中星像的位置和光度等信息和已知星表中的相应位置和光度的对象作匹配。当图像中星的数量较少时，这种匹配是容易实现的。然而，对于大视场或密集星场的多目标的快速匹配却并非易事。

另外，由于拍摄星图像时所用的滤光片不同或曝光时间和分辨率不同导致同一天区所拍摄的星图也不一样，即所拍摄的图像中的星和星表中的星不完全一样。如果所拍摄的图像中有而星表中没有的星，我们把它记为额外的星，相反，如果所拍摄的图像中没有而星表中却有的星，我们把它记为丢失的星。匹配过程中除了必须处理那些额外的星和丢失的星，还必须处理平移、旋转和由温度引起的微小焦距尺度的变化。

目前，已经提出了多种星像配准算法。Groth首次提出了基于三角形的匹配算法[4]。他通过限制三角形中最长边与最短边的比率在一个用户定义的范围内来减少所构造的三角形的个数，从而减少匹配的时间。此算法在匹配阶段的时间复杂度是O(n4.5)，这里的n是列表中星的个数。Murtagh提出了一种基于坐标对集合特征的方法[5]。这种算法的匹配是基于两个列表中与坐标对相关的特征向量。Murtagh的算法在匹配阶段的时间复杂度是O(n2)。Valdes等人提出了一种自动的星表匹配算法[6]。通过提取含有量度坐标和星等的两个或多个星表，然后再匹配它们。其算法是取出星表中较亮的对象，然后找出一个星表到参考星表之间的坐标变换，这样星表中所有的对象都可基于变换后的参考坐标进行匹配。Pal和Bakos描述了另一种基于三角形的方法[7]。此方法通过裁剪使得其在大视场中也非常高效，尽管大视场中有大量的点源或者较大的非线性扭曲。其程序是基于新定义的三角形空间中的对称点进行匹配的。2007年Tabur提出了两种快速的星图匹配算法[8]：基于三角形空间的方法和基于向量的方法。作者的研究还表明后者要快于前者。最近，Zhang等人又提出了基于径向和环向特征的星图匹配算法[9]。Tabur的方法主要是针对星图中的星比较密集的情况，而Zhang等人的方法主要是用于天文导航。针对这两种不同的星图匹配算法，我们进行比较分析。

文章的内容是这样安排的：第1节介绍了基于向量的方法；第2节描述了基于径向和环向特征的方法；第3节给出了两种方法实验结果的对比分析；最后一部分是结论。

1 基于向量的方法

按照Tabur的思想，基于向量的方法主要是通过严格的形状定义来构造形状特征集。期望通过匹配每个特征集来减少可能发生的误配，尽快找到正确的匹配点。一旦有一个特征集匹配成功就可以停止匹配，避免了匹配整个列表和不必要的计算。

1.1 构造点对

对于所拍摄的图像，首先用定心算法测量每颗星的位置及星等。因为亮星能够提供更加准确的信息，所以把测得的所有星按星的亮度降序排列，选择前n颗亮星构成一列表，记为I。它表示这些星来自图像。而已有的星表能够提供关于星的准确信息，所以从某一星表中提取亮度高于一定星等的星的基本信息(赤经、赤纬和星等)构成另一列表，记为R。它表示源于参考星表。我们期望从列表R中所选的n颗亮星都能在列表R中找到与自己所对应的星。然而，实际情况并非如此。因为额外的星和丢失的星造成两个列表只有一部分重叠。增大列表R可以增大匹配概率，代价就是更长的点对列表构造时间。和以前的方法不同的是，增加列表的大小并不显著增加点对匹配的时间。

常用的定心算法有Gauss拟合法、中值法、矩方法(包括修正矩方法)和寻导法等[10]。在实验中采用Gauss拟合法来获取星像的中心，用星表UCAC2[11]来获取星像的信息。据李展等人的研究，在上述经典定心算法中，与修正距方法和中值法相比，Gauss拟合法是精度最高的一种定心算法[12]。而UCAC2是一部星像密度和位置、自行精度相对较高的星表。

具体地说，为了减少可能发生的误配，仍然需要严格的形状定义来保证在几乎常数的时间里产生一个成功的匹配。首先从星像列表I中取出用户定义的m颗亮星来构造我们所定义的形状，构造过程通过把m颗亮星中的第一颗亮星A作为坐标的中心，而其它的星B、C、D，…按照相对于A点的坐标构造而成，并计算它们的角距离和位置角。在匹配过程中可能需要构造多个由m颗星定义的形状特征集来进行匹配，一旦匹配成功就停止构造。定义计算位置角的参考方向朝北，顺时针旋转为角度增加的方向，如图1。角距离：dad=dAD/F.

(1)

其中dAD是所拍摄图像中的两颗星A与D之间的距离，以像素为单位；F为焦距；dad是星表中与A和D对应的两颗星之间的距离，以弧度为单位。这里假定在列表R中的位置信息已经从天球投影到了成像的图像平面。

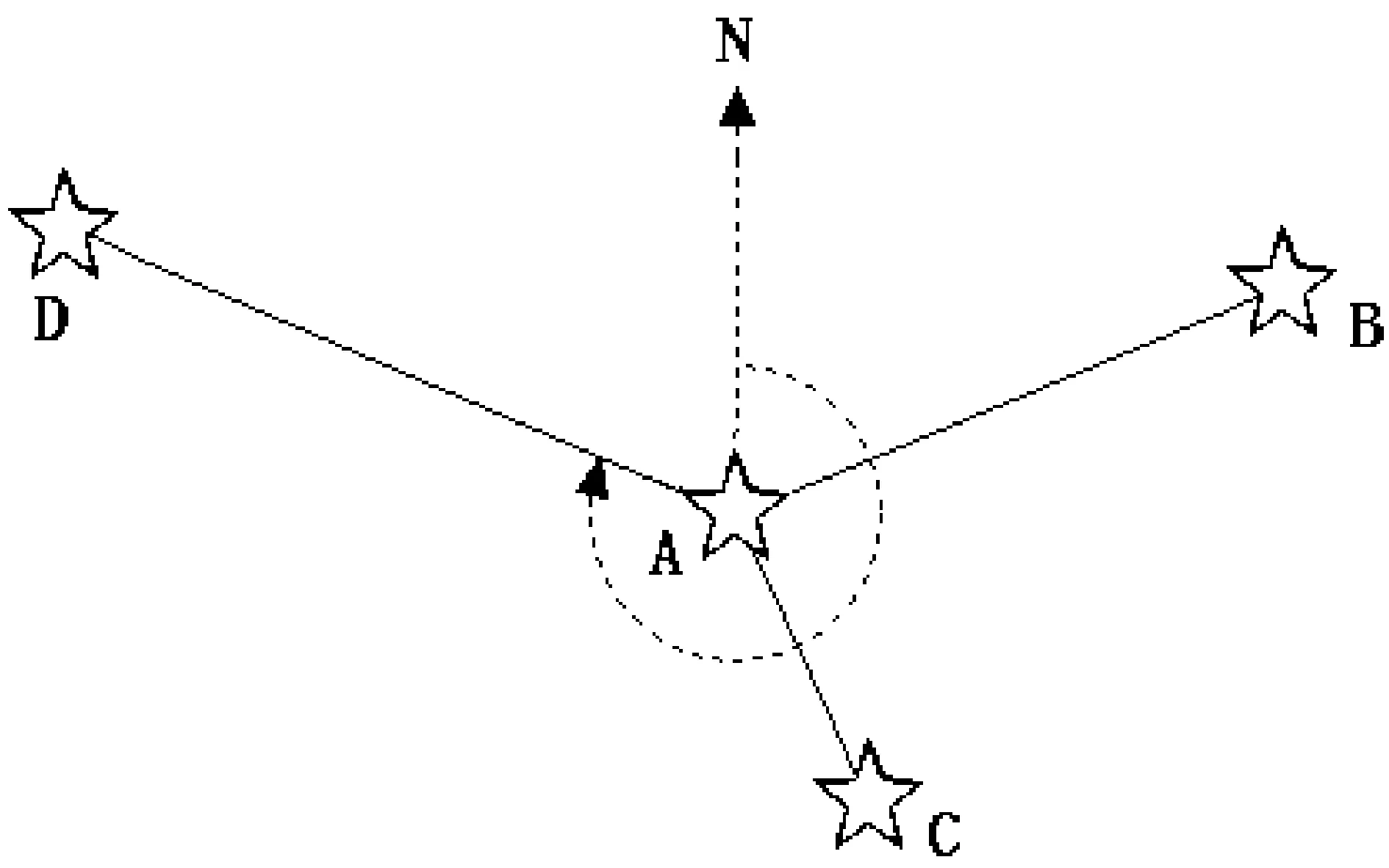
图1 使用用户定义的m颗星来构造预先定义的形状

从列表R中取出前n颗亮星构造点对列表，则n颗星总共可构造的点对数为：

P=n(n-1)/2

(2)

构造点对列表的目的是提供星表中点对的相关信息，以供图像中的点对进行搜索匹配。为了加快搜索速度，先按照角距离对所构造的点对列表进行排序，位置角也同样会被排序，因为它和角距离是一一对应的。这种方法只需要构造一个点对列表，而且所构造的点对数目远远小于传统的三角形方法所构造的三角形数目[8]。

1.2 匹配点对

这个匹配的过程就是从所构造的点对列表中找出与AB、AC、AD… 所对应的点对，而它们每一对是否匹配要靠角距离和位置角来确定。对于第一个m颗星所构造的形状特征集，首先从点对列表中找出与AB匹配的点对，用二分查找来快速定位匹配点对，如果查找到的点对与AB的角距离之差在所给的误差范围内，将首先定义图像与星表之间的旋转角为AB与其匹配点对的位置角之差，每个形状特征集只定义一次。因为图像和星表中位置角的不同是由于探测器的旋转造成的，所以后面的AC、AD…与其匹配点对之间的旋转角也应该和AB的一样，如果偏差大于1°就会被认为是不匹配的。如果找不到一个点对的角距离与AB的角距离之差在预先给定的误差范围内，AB将会被拒绝，转而进入下一个点对AC的查找。

一旦m个候选点被识别，这m个点就会被用来求解底片常数(这里采用6常数模型)。如果底片常数正确，则匹配成功。否则说明这m个点中存在某些误配点，这时将用一个函数来循环找出正确匹配的点，剔除错误匹配的点。如果m个候选点中正确匹配的点数小于3，则调用此函数会失败。因为至少需要3个点才能确定图像和星表之间的对应关系，用下一个m颗星所构造的形状特征集来继续这个过程。这个过程将重复进行直到有足够多的星被识别为止，否则就是匹配失败。

2 基于径向和环向特征的方法

按照Zhang等人的研究[9]，基于径向和环向特征的匹配算法是将邻域伴星的几何分布特征分解成径向特征和环向特征来构成特征模式，并建立相应的特征模式库。径向特征具有构造简单和旋转不变性，是一种比较可靠的特征，所以用径向特征作初始匹配，用环向特征作后续匹配。

2.1 构造径向特征

径向特征的构造方式如下：

(1)如图2(a)所示，以星S为主星，在半径为Rr邻域内的星均称为S的伴星(共有NS颗)。沿径向方向量化(设量化等级为Nq)，即将以S为中心以Rr为半径的邻域划分成间隔相等的环带G1,G2,…,GNq。

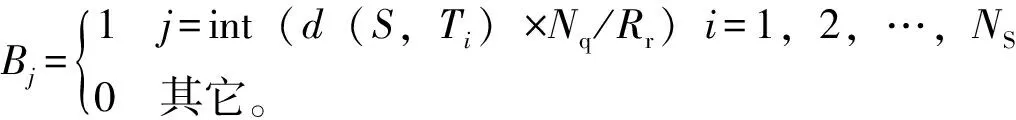
(a) 径向特征，其中 (b) 环向特征

Rr为特征模式半径，Nq为量化等级Rc为特征模式半径

NS为Rr半径邻域内星的个数

图2 径向特征和环向特征示意图

Fig.2 Illustration of the definitions of quantitative characteristics varying along radii and circumferential directions(in (a)and(b)),respectively

2.2 构造环向特征

(1)如图2(b)所示，以S为主星确定环向模式半径Rc，依次计算伴星之间的夹角，如图2(b)中的∠T1ST2,∠T2ST3,∠T3ST1(其T1,T2,T3为S的伴星)。

(2)找出最小夹角(如图中的∠T1ST2)，并用它的一边(ST1)作为起始边对圆形邻域作环向划分，将圆周等分成8个扇区。由所有伴星在各象限上逆时针方向的分布组成一个8bit的向量v。如图2(b)所示v=(11000100)。

(3)将v作循环移位，找出v所组成的数(十进制)的最大值，将这个最大值作为S的环向特征。如图2(b)所示v循环移位后环向特征向量patc(S)=(11000100)=196。

2.3 构建导航数据库

导航数据库包含两部分：参考星表和导航星模式库。参考星表包含从基本星表中提取的亮度高于一定星等的星的基本信息(赤经、赤纬和星等)。导航星模式库由特征构造过程所生成的特征模式向量构成。这里先用径向模式特征作初始匹配，因此必须先构建径向模式向量的导航星模式库。直接存放径向特征模式向量会造成匹配搜索速度慢，所以这里采用查找表的形式构建径向特征模式库。经过初始匹配后，可得到一个候选匹配星的集合，再构造环向特征作后续匹配。

2.4 匹配特征向量

基本思想是先利用初始匹配(粗匹配)将搜索范围限定到一个较小的量级，然后用其他的特征逐层筛选，直到获得最终的正确匹配。

2.4.1 初始匹配

2.4.2 后续匹配

理论上，如果存在两颗以上的观测星对应的候选匹配星唯一，则可进入验证识别阶段。如果C中存在大量的冗余匹配，将用环向特征对其作进一步的筛选。如果观测星图的环向特征和导航星模式库中的相同，则保留该候选匹配星，否则剔除。

2.4.3 FOV约束

如果经过前面的筛选后候选匹配星仍不唯一，将采用FOV约束对其作进一步筛选。FOV约束基于这样一个假设：当前观测星图中所有星的正确匹配包含在C中，而且它们还应该集中在某个FOV的限制区域内，而那些不正确的匹配(错误匹配和冗余匹配)则随机分散在全天球范围内。基于这一假设，对C进行扫描，如果某候选匹配星一定邻域半径r内星的个数少于某一个阈值T，则将其从C中剔除。

3 实验结果对比分析

为了对两种方法进行比较，利用云南天文台1m望远镜所拍摄的多幅图像进行了匹配，并对匹配过程进行了粗略的时间测定。具体地，使用了星团NGC2168和NGC1664的观测图像，详细信息见表1。图3给出了星团NGC2168观测时一帧典型的CCD图像，画圈的表示已匹配的(在UCAC2中)星。表2给出了第1种方法对于NGC2168中不同大小列表所花费时间的统计。它包括列表中星的颗数(n)、构造点对的平均时间、匹配点对的平均时间、匹配过程平均总耗时及匹配率。表3给出了第2种方法对NGC2168中不同大小列表所花费时间的统计。它也包括列表中星的颗数(n)、构造特征向量的平均时间、匹配特征向量的平均时间、匹配过程平均总耗时及匹配率。

表1 所使用的资料集说明

图3 匹配好的NGC2168图像

n 构造点对(ms)匹配点对(ms)总耗时(ms)匹配率%1000330305219588592001880398261899163003490485339899804006480661482810050104508665589100601505112161511008027891626899610010045992026147561001501076429912121210020018986441426889100

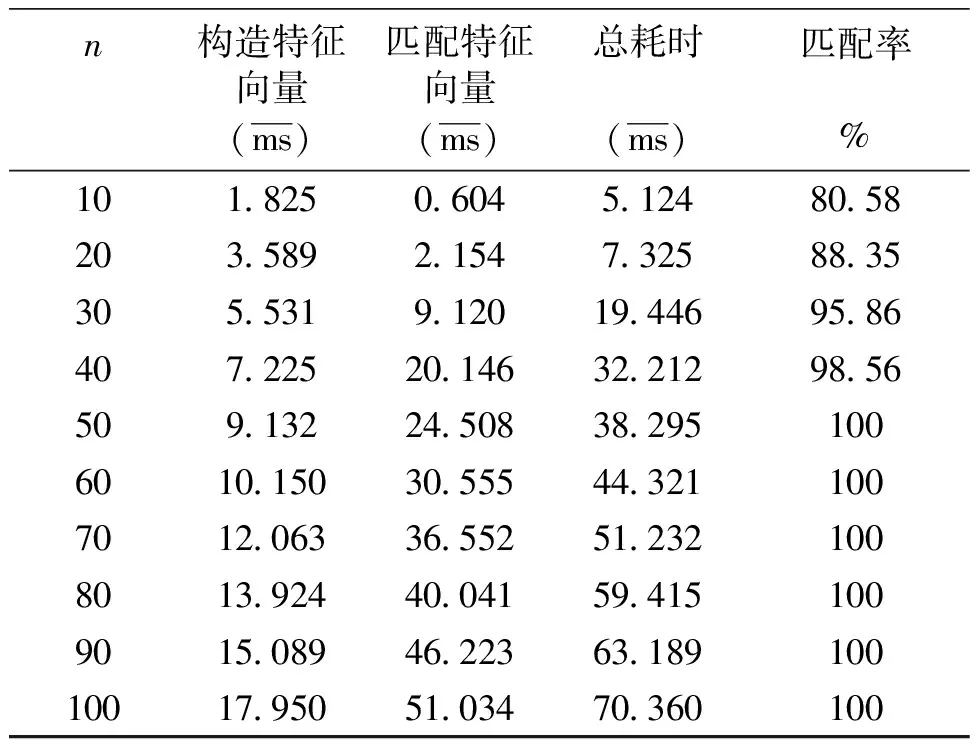
表3 方法2处理NGC2168图像用时统计

图4描绘了对于NGC2168星团，方法1中点对的匹配时间相对于点对构造时间的对比。从图中可以直观看出，当n较小时，构造点对所花费的时间几乎是可以忽略的，匹配点对占大部分时间。但随着n的增加，构造点对所花费的时间急剧增加，而匹配点对的时间却接近于一个常数。显然构造点对占据了绝大部分时间。

图5给出了对于NGC2168星团，基于径向和环向特征的方法在构造特征向量和匹配特征向量阶段的时间对比。发现当n较小时，匹配特征向量所花费的时间是很小的，但随着n的增加，匹配特征向量所花费的时间却陡然增加，说明此方法的时间主要花费在此阶段。

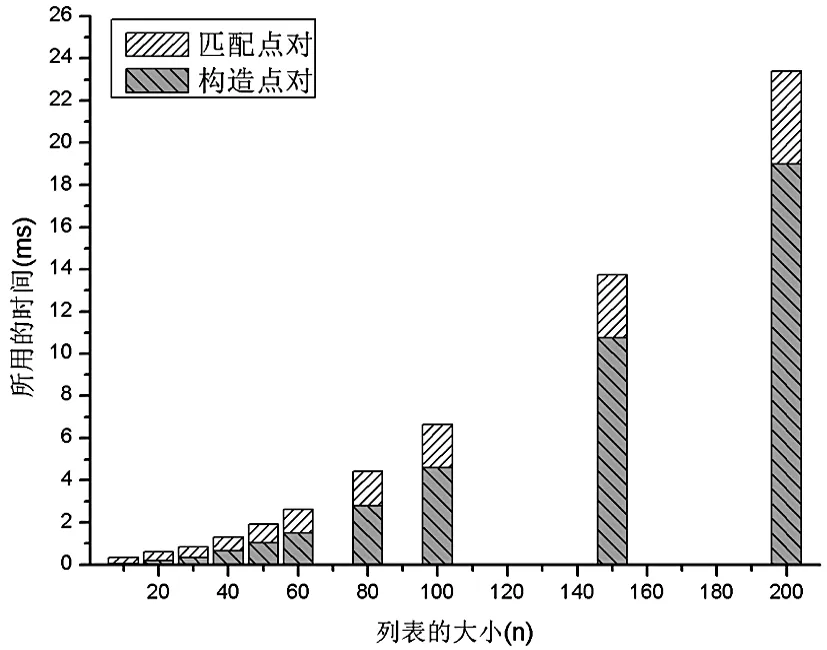
图4 NGC2168中构造和匹配点对所用的时间对比

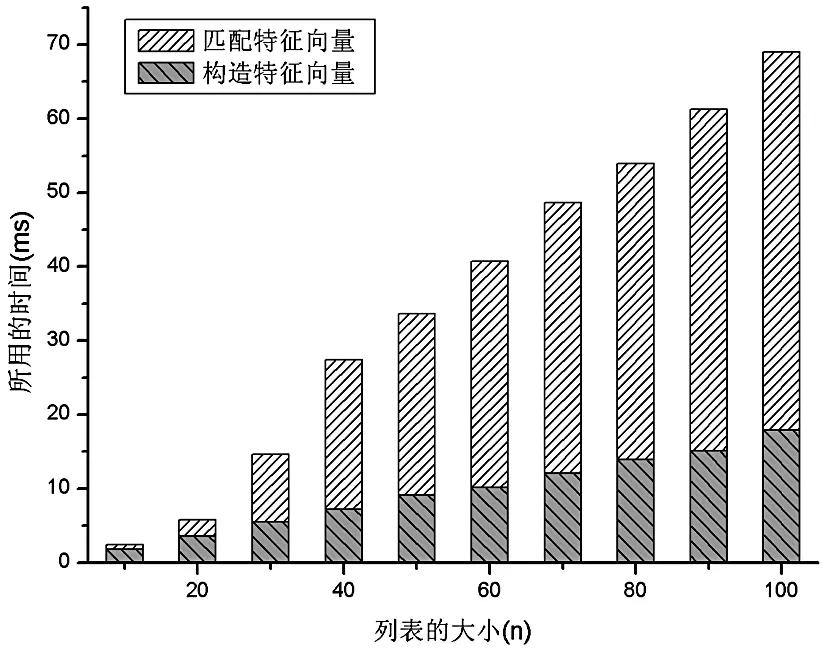
图5 NGC2168中构造和匹配特征向量所用的时间对比

图6给出了两种方法在匹配阶段及整个匹配过程所花费时间的对比。由于不同的人所使用的机器不同或者是所使用的列表大小不一样等原因，所以绝对的运行时间是没有可比性的。

图6 NGC2168中两种方法的对比(方法1：基于向量的方法，方法2：基于径向和环向特征的方法)

图7给出了星团NGC1664观测时一帧典型的CCD的图像，画圈的表示已匹配的(在UCAC2中)星。表4给出了第1种方法对于NGC1664中不同大小列表所花费时间的统计。表5给出了第2种方法对于NGC1664中不同大小列表所花费时间的统计。

图7 匹配好的NGC1664图像

n 构造点对(ms)匹配点对(ms)总耗时(ms)匹配率%1000630345238586692001600458291895963003701535399898984006851961487810050108024565719100601607292169911008030153647901610010046754016150561001501098849112315210020019997558428421100

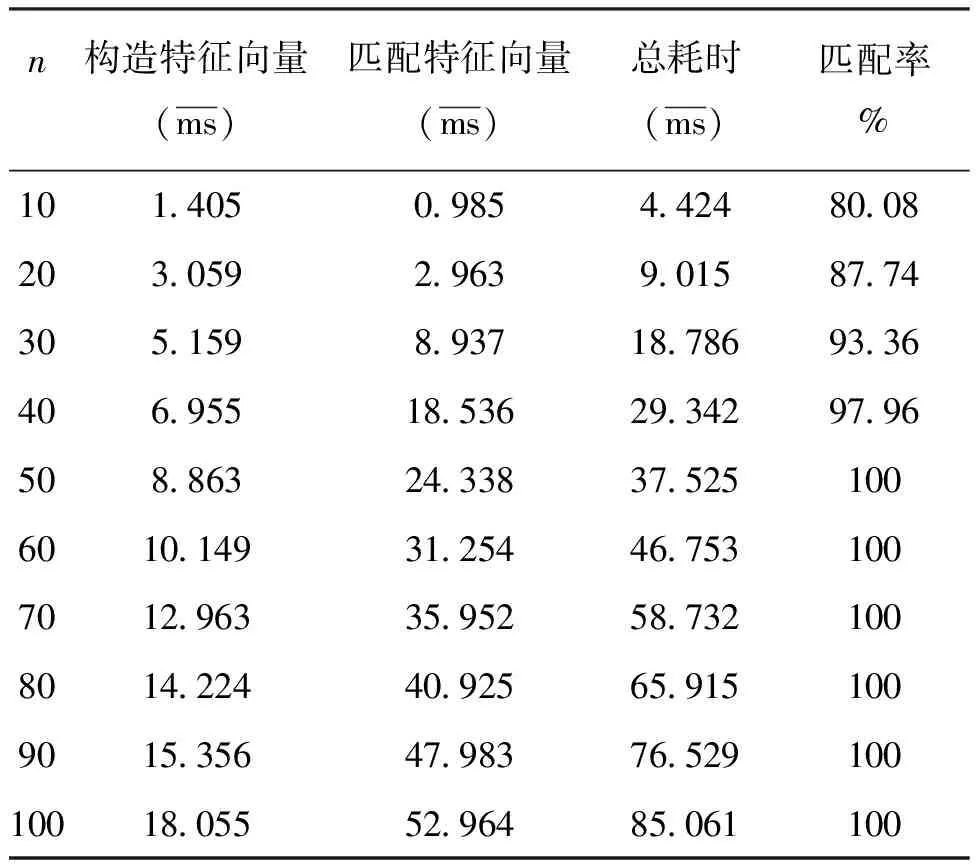
表5 方法2处理NGC1664图像用时统计

图8描绘了对于NGC1664星团，方法1中点对的匹配时间相对于点对构造时间的对比。图9给出了对于NGC1664星团，基于径向和环向特征的方法在构造特征向量和匹配特征向量阶段的时间对比。图10给出了NGC1664中两种方法的对比。可以看出，和NGC2168的测试结果基本相同。

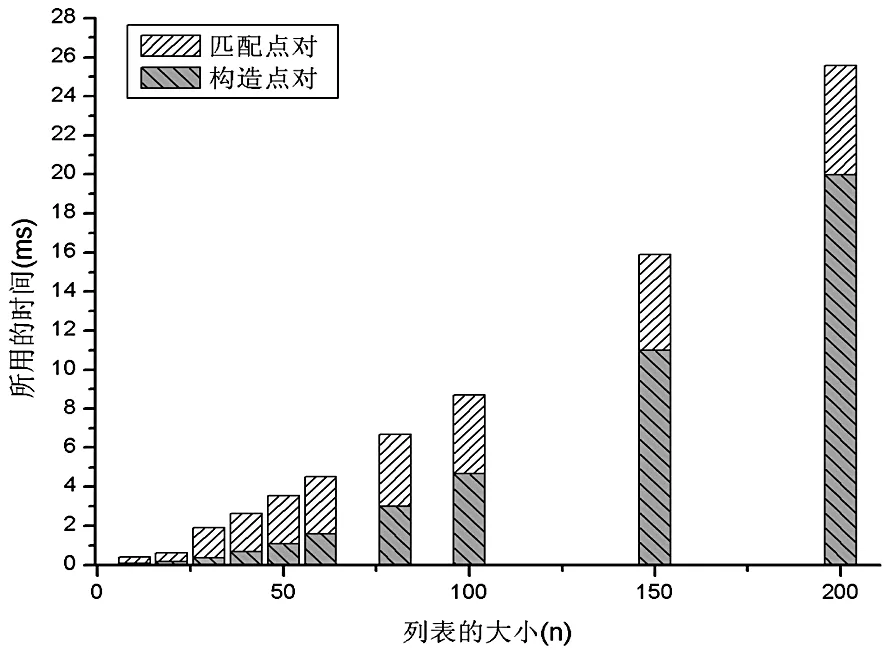
图8 NGC1664中构造和匹配点对所用的时间对比

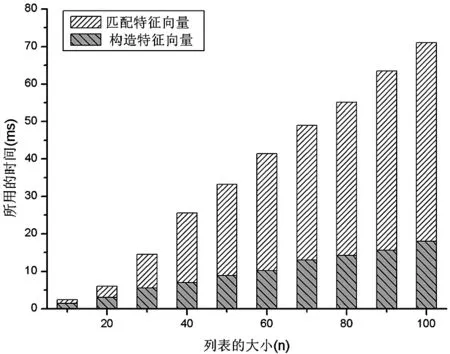
图9 NGC1664中构造和匹配特征向量所用的时间对比

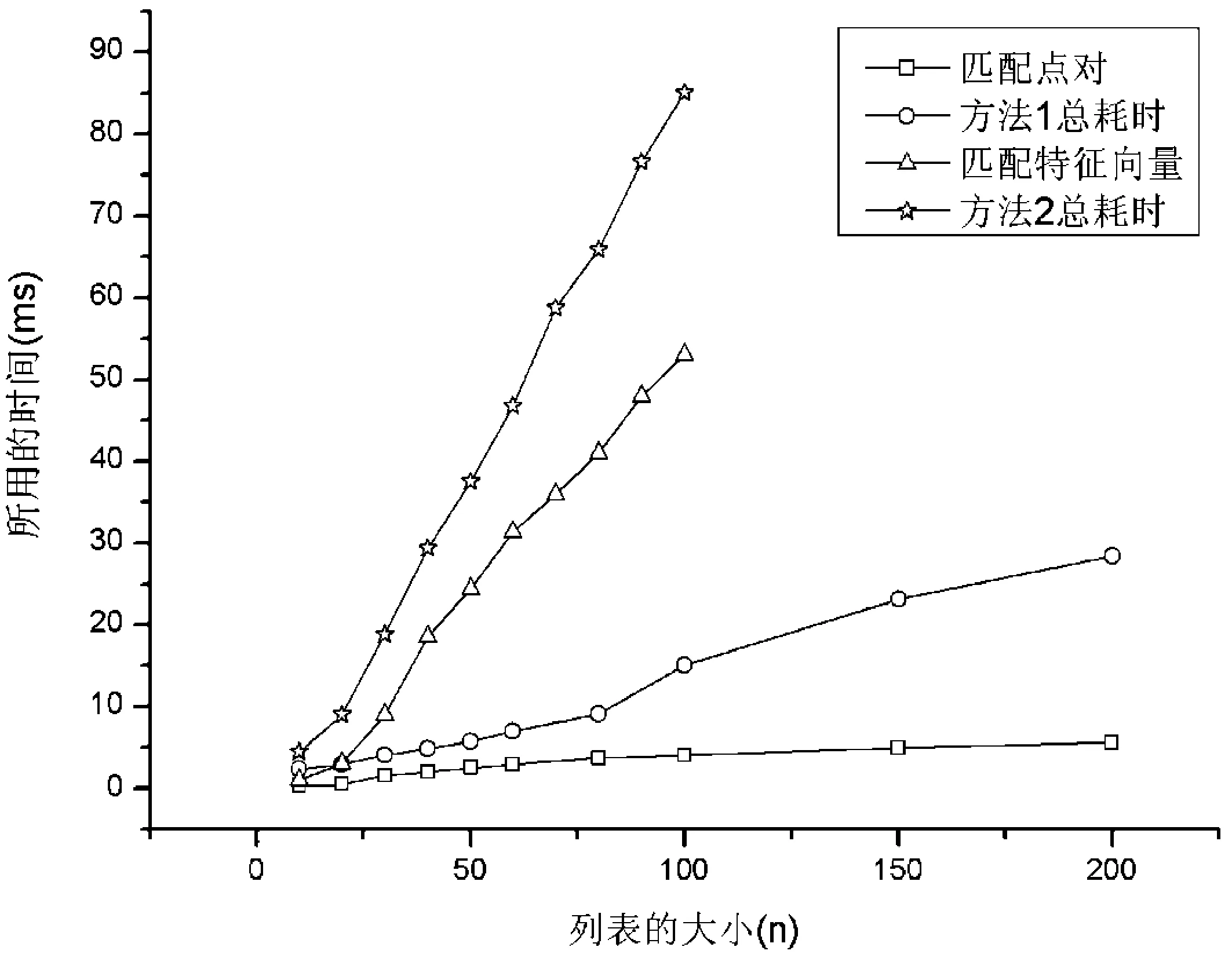
图10 NGC1664中两种方法的对比(方法1：基于向量的方法，方法2：基于径向和环向特征的方法)

4 结 论

本文采用基于向量的方法和基于径向和环向特征的方法对实际的天文图像进行了匹配。通过对NGC2168和NGC1664的大量图像进行匹配，结果都表明基于向量的方法更优，它在匹配阶段所需时间几乎是一个常数，独立于列表的大小，而基于径向和环向特征的方法在匹配阶段耗时较多。

致谢：感谢孟小华副教授，张庆丰副教授在本文研究过程中提出的建设性意见。

[1] Stetson P B. DAOPHOT: A computer program for crowded-field stellar photometry[J]. PASP,1987, 99: 191-222.

[2] Schechter P L, Mateo M, Saha A. DOPHOT, A CCD photometry program: description and tests[J]. PASP, 1993, 105:1342-1353.

[3] Bertin E, Arnouts S. SExtractor: Software for source extraction[J]. A&AS, 1996, 117:393-404.

[4] Groth E J. A pattern-matching algorithm for two-dimensional coordinate lists[J].AJ, 1986, 91: 1244-1248.

[5] Murtagh F. A new approach to point-pattern matching[J]. PASP, 1992, 104:301-307.

[6] Valdes F G, Campusano L E, Velasquez J D, et al. FOCAS automatic catalog matching algorithm[J].PASP, 1995, 107: 1119-1128.

[7] Pal A, Bakos G A. Astrometry in Wide-Filed Surveys[J]. PASP, 2006, 118:1474-1483.

[8] Tabur V. Fast algorithm for matching CCD images to a stellar catalogue[J]. PASA, 2007, 24:189-198.

[9] Zhang G J, Wei X. G, Jiang J. Full-sky autonomous star identification based on radial and cyclic features of star pattern[J].Image and Vision Computing, 2008,26：891-897.

[10] Stone R C.A Comparison of Digital Centering Algorithms[J].AJ,1989, 97：1227-1237.

[11] Zacharias N，Urban S E, Zacharias M I , et al. The Second US Naval Observatory CCD Astrograph (UCAC2)[J].AJ, 2004, 127：3043-3059.

[12] 李展，彭青玉，韩国强，CCD图像数字定心算法的比较[J].天文学报，2009, 50(3): 340-348.

LI Zhan,PENG Qing-yu,HAN Guo-qiang.Comparison of Digital Centering Algorthms Based on CCD Images[J].Acta Astronomica Sinica,2009,50(3):340-348.