浅谈数据校正在企业能源计量管理中的应用

何 红,谢秋风

(1.中石化仪征化纤股份有限公司动力部,江苏仪征 211900;2.上海慧时软件有限公司,上海 200233)

0 引 言

随着流程工业企业中对计量管理要求的提升, MES计划调度系统的应用对装置进、出料的平衡控制,对能耗、单耗考核提供有价值的数据要求,装置间的计量管理等多种要求,将各种测量仪表的数据通过计算机控制系统(DCS等)集成到工厂局域网实时数据库中进行计量管理,以达到优化装置产能,取得最佳经验效益的目标。该文以某石化公司在内部主干局域网络的基础上新建了一套计量信息集成管理系统为例,详细地介绍了系统的建立方法,并简单介绍了多种技术的集成方法,串口设备与以太网互联通信技术、数据库构建技术、SCADA/HMI技术以及客户/服务器技术等。

计量信息集成管理系统在实际应用中不可避免的问题:计量仪表客观存在的测量误差,使能源供用双方的测量数据存在不同程度的误差。该文主要介绍以数据校正技术为核心的全厂能源平衡系统,基于能源供用双方机理和统计分析方法实现测量数据的校正计算,估算未测变量及存在的偏差,解决能源计量由于供用双方一,二次表计量存在基本误差导致数据不准确、不一致、不完整和管损等问题,通过将实时过程数据提炼成一致的、可靠的高质量生产管理信息,为监控、优化、计划调度及决策分析提供坚实的基础。

1 数据校正技术基础

由于实际生产制造和测量过程中的一些问题,造成了测量数据含有误差,不能满足工艺过程的能量平衡和其他约束条件。为此,需要对测量数据进行数据校正处理。一个完整的数据校正过程包括:稳态检测、数据分类、过失误差检测与处理和数据协调(参数估计)等步骤。

过程数据校正的任务是检测过失误差、校正带随机误差的测量数据并估算出一些未测变量,即数据协调与过失误差检测。过程处于稳态是实施稳态数据校正的前提条件,检测过程稳态变化的方法业已成熟,对于时间尺度为“日”的厂级物料平衡而言,准稳态的假定通常能得到保证。

2 数据校正模型建立

结合动力生产中心蒸汽输送管网流程图(如图1所示),详细讨论数据校正技术在蒸汽计量系统中的应用,并介绍了基于蒸汽流量平衡的数据校正流程和算法。

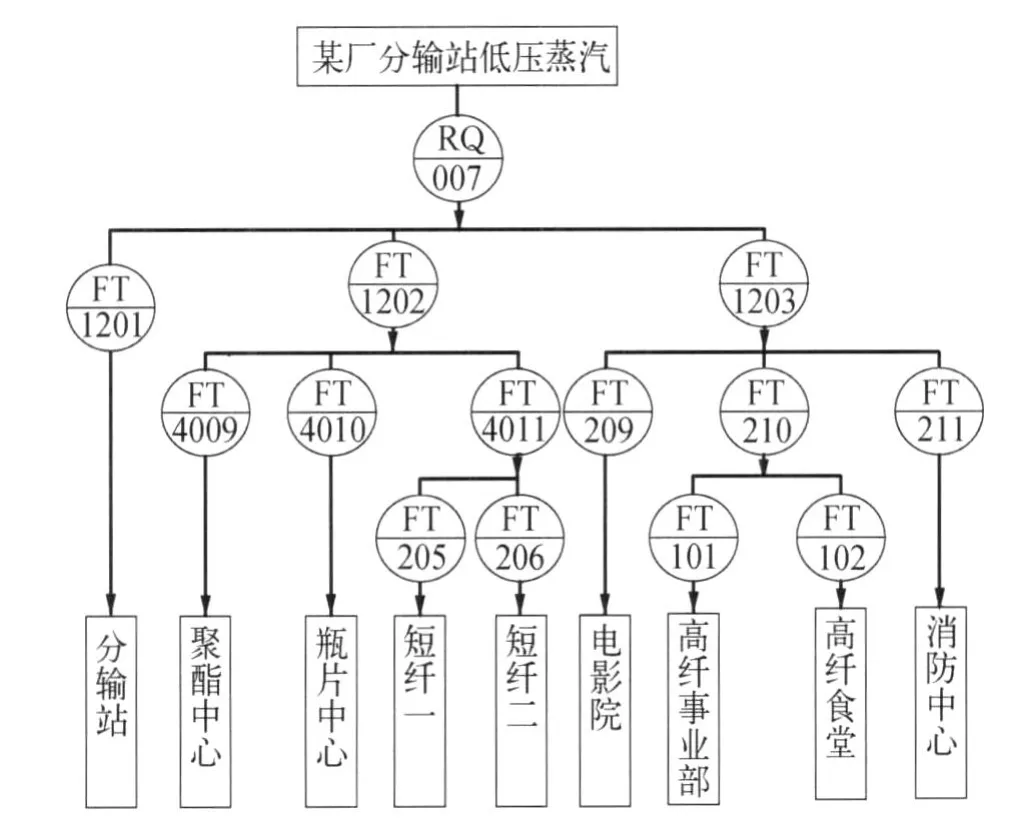
图1 动力生产中心低压蒸汽网络

高温高压蒸汽通过管道输送给用户的过程中,流量计量是生产能耗统计、监管的基础,只有在数据质量达到一定的准确度之后,再进行进一步的优化控制、绩效评估才有实际意义。在实际生产中,除了设计合_理的输送管网,采用精度可靠的仪表以_外,根据质量守恒定律,建立管网中各个变量的约束关系,然后通过数据校正得到一组符合约束模型的校正值,可以有效地提高数据的准确度。

根据仪表计量的相关规定,量程(或读数)与精度的乘积可以作为仪表的相对误差,即在仪表的相对误差范围内对仪表读数进行调整是合理的,因此采用仪表量程与精度的乘积作为每个仪表测量值的可调范围约束。

在数据协调中,协方差矩阵的选取决定了每个变量进行调整的权重,原则上对于精度较高的仪表分配较高的权重。结合蒸汽计量的实际情况,采用仪表测量值的倒数作为协方差矩阵主对角元素的值。采用该矩阵可以保证同样的调整幅度,对于测量值较大的仪表来说其调整幅度较小。经实践验证,通过如此方式得到的校正结果十分接近生产实际情况。按上述方法,各个变量的调整范围、权重系数和变量名称定义见表1所列。

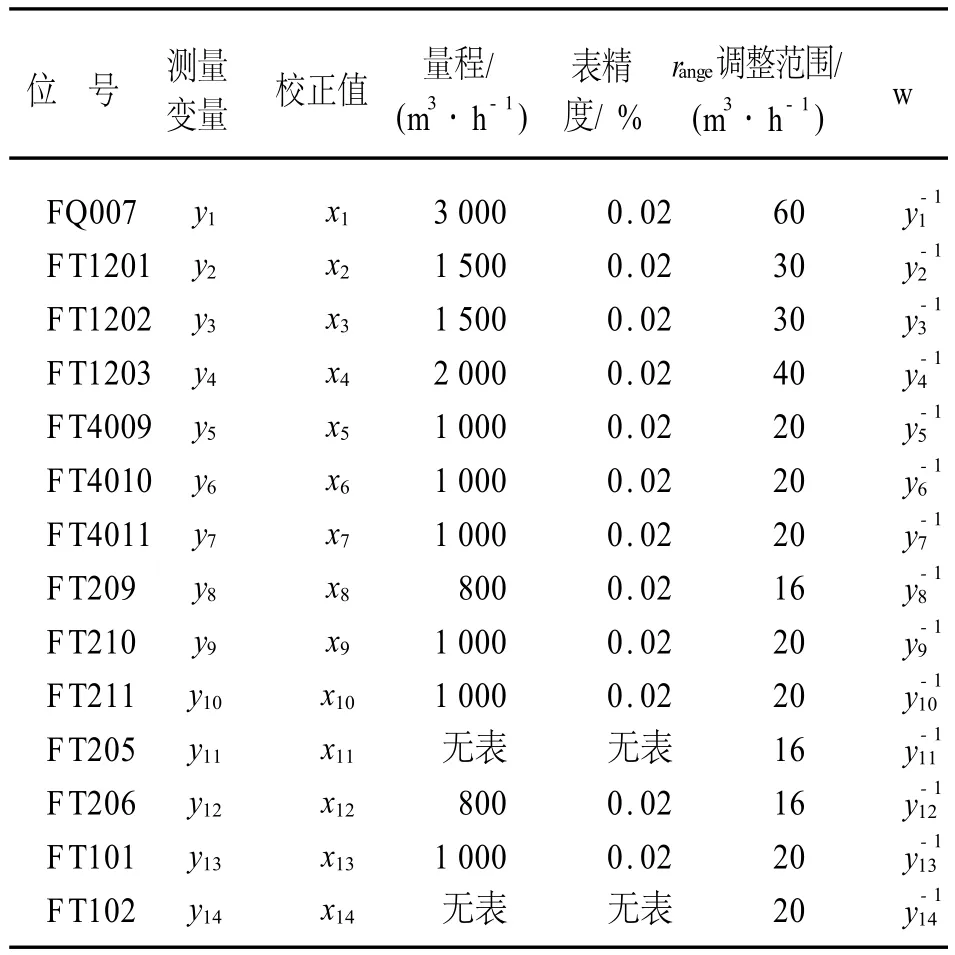
表1 变量定义说明

根据表1和图1,最终得到该蒸汽管网图的数据校正模型如下:

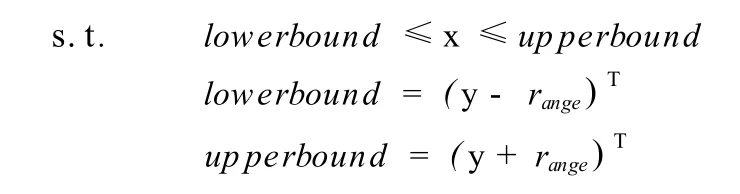
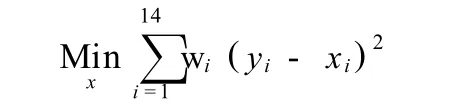
式中

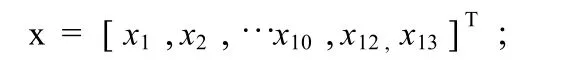
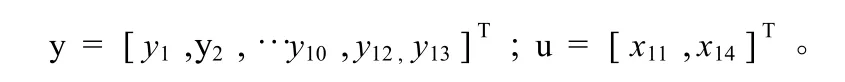
3 数据校正算法

3.1 算 法

在实际情况中,由于经济成本、现场环境等因素,不可能对所有的变量进行测量,而是根据实际情况建立如下约束矩阵方程

式中 x——n×1维测量变量真实值;Ax——相应的m×n维约束矩阵;u——p×1维未测量变量真实值;Au——m×p维约束矩阵;c——m×1维已知的常系数列向量。

目标函数为

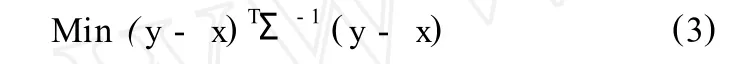
式中 Σ——测量变量协方差矩阵;y——n×1维测量变量测量值。

这样,数据校正问题的解等价于求方程式(2), (3)组成的二次优化问题的解。

在二次优化问题过程中,首先要构造投影矩阵P,将未测量变量从约束方程式(2)中消掉。采用将Au进行Q R分解的方式构造P矩阵,同时还可以进一步将测量变量分为冗余测量变量和非冗余测量变量,将未测量变量分为可观测未测量变量和不可观测未测量变量。具体过程如下。

3.1.1 构造投影矩阵 P

将Au进行Q R分解,可以得到

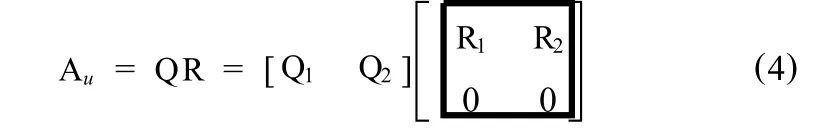
式中 Q——m×m维正交矩阵;R——s×s维非奇异上三角矩阵,且s为构成Au的列向量中线性无关的个数。将式(4)代入式(2),然后两边同时乘以QT2得

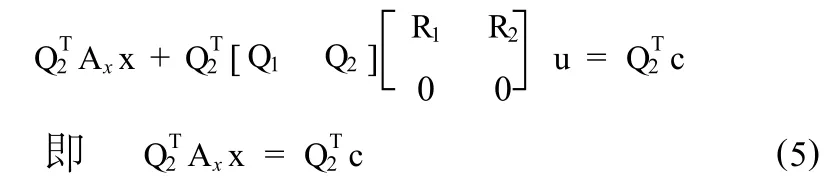
所以QT2即为所求的投影矩阵。由式(2),(5)组成的最优化问题等价于式(2),(3)组成的二次优化问题,通过拉格朗日乘子法得到测量冗余变量的调整值为

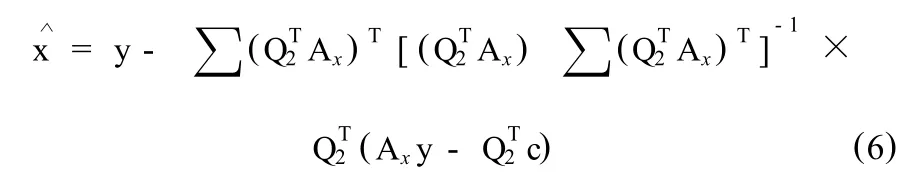
3.1.2 未测量变量估计

将式(4)代入式(2),然后两边同时乘以QT得

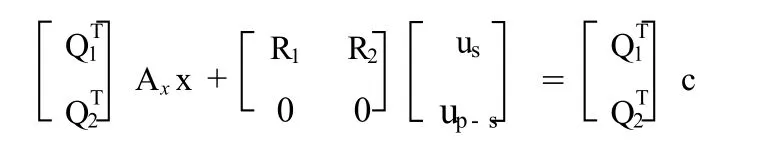
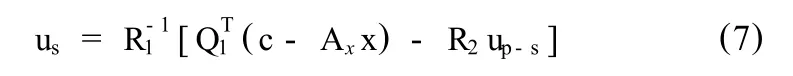
3.2 数据协调流程

图1中的节点处不可能都装有测量仪表,对于某些用量比较小的用户来说,安装仪表的经济成本甚至高于蒸汽本身产生的经济效益。采用数据校正技术不仅得到了测量变量的校正值,而且可以利用约束方程对未测量值进行合理地估计。结合蒸汽计量系统数据校正模型,采用如下数据协调未知参数估计流程:

a)根据蒸汽计量管网图和质量守恒定律,建立约束模型方程,然后根据各个测量仪表的精度和量程得到每个测量变量的上下界,从而得到变量的不等式约束方程。

b)通过对Au进行Q R矩阵分解得到投影矩阵,利用该矩阵将未测量变量从原问题分离出去,将原问题转化为只含有测量变量的带不等式约束的稳态数据校正问题。

3.3 过失误差侦破流程

在实际生产过程中,随着仪表使用年限的增加,加之恶劣的工作环境,蒸汽计量网络系统中经常出现仪表故障等现象。因此产生的过失误差如果得不到及时地侦破,会在数据协调过程中通过约束模型的变量相关性,影响到其他正常的变量,从而导致整个网络计量所得到的数据大大偏离客观实际,影响蒸汽流量计量质量,所以过失误差侦破流程不可或缺。

过失误差侦破一般可选 GT,GLR两种算法。GT算法利用系统平衡残差和协方差矩阵构造统计变量,计算方便,而且检验出过失误差的概率比较高,但无法对过失误差进行定位和补偿。GLR算法可以根据过失误差模型,辨识系统中的过失误差类型,对误差进行定位和补偿,但计算量比GT法大。

基于此基础,结合蒸汽计量网络的流程特点,蒸汽系统过失误差侦破采用了GT-GLR联合法,对系统中的过失误差进行侦破、补偿。综合 GT法和GLR法的优点,通过将GT法和GLR法结合起来,提出了基于顺序补偿原理的多显著误差侦破算法。该算法在每次补偿运算之前先利用GT法判断系统中是否存在过失误差,如果存在则利用 GLR法定位出现过失误差可能性最大的变量并进行在线补偿,反复计算直至系统中没有过失误差存在。

4 数据校正技术流程

依据上述蒸汽数据校正算法,蒸汽计量网络中的数据校正流程如图2所示,用以解决实际应用中蒸汽流量计量系统中的数据不平衡和不完整的问题。

5 采用数据校正技术后的效果

通过采用数据校正技术,蒸汽计量网络中的数据质量已经得到了显著的提高。在此基础上工艺人员通过设计、优化蒸汽管线,减少蒸汽传输过程中的损失以及加强使用环节中的节能意识进一步降低蒸汽能耗,减少浪费。

实施数据校正技术后各生产中心的不平衡计量偏差有了明显的下降,以聚酯中心为例,平时偏差大多落在5%～10%内,实施数据校正技术后,装置损耗率基本在3%上下波动。由此看出数据校正技术实施后,减少了随机误差对统计的影响,各生产中心的物流平衡均得到了较大幅度的提高。

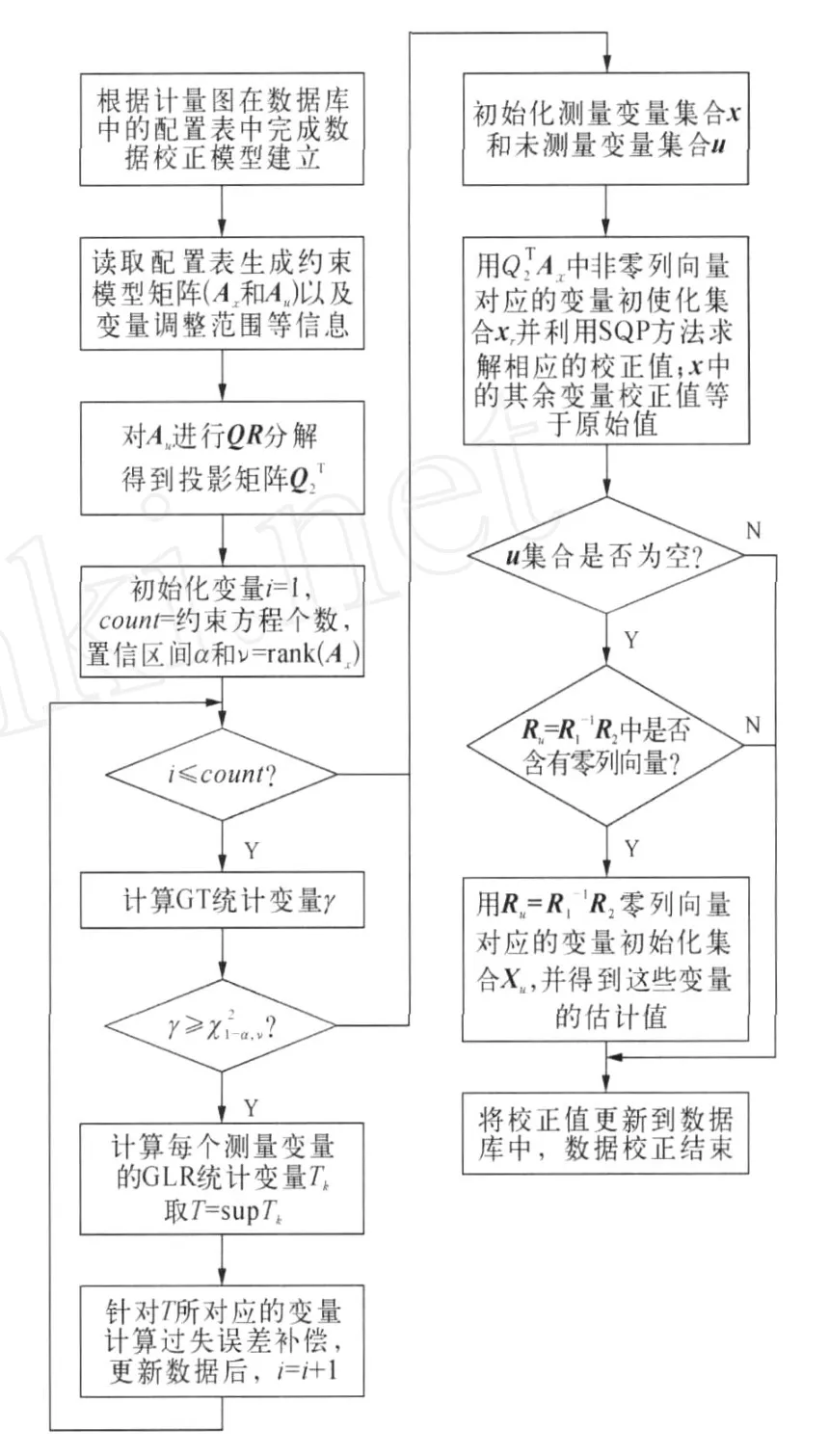
图2 数据校正技术流程

6 结束语

通过计量信息集成管理系统的Web发布功能,企业的生产管理人员通过浏览能源平衡报表以及各种计量点的数据能快速准确地掌握企业的生产经营状况以及其中存在的问题(如有助于发现现场计量仪表读数异常,人工录入数据偏差等),用于指导生产和与其他部门沟通,取得了很好的应用效果。

数据校正系统已在该公司的能源计量平衡中得到了实际应用,在网络系统和实时数据库平台正常运行的情况下基本实现了数据显著误差检出率大于95%;日报和月报流量统计数据精度提高了5%。

[1] 杨自奋,洪 波,罗 伟,等.蒸汽系统的优化设计和运行[J].能源技术,1996,(1):16-20.