基于马尔科夫模型的“二取二”结构误跳车分析

于改革,陈学东,,朱建新,包士毅

(1.浙江工业大学化工机械设计研究所,杭州 310032;2.合肥通用机械研究院,合肥 230031)

0 引 言

安全联锁系统主要由传感器、逻辑运算器和最终执行机构组成,在紧急状况下执行安全功能(Safety Function)以达到控制风险的目的。根据标准IEC 61511和ISA S84.00.01-2004规定,安全联锁系统中仪表主要有两种基本的失效模式,即安全失效和危险失效[1-2]。衡量这两种失效分别用平均无安全故障工作时间M T T Fs(Mean Time To Failure Spurious)和指令模式下的平均危险失效概率 PFDavg(Average Probability of Failure on Demand)。对于安全联锁系统,在紧急情况下不能执行预设功能会造成严重的后果。而安全功能的不恰当执行,即当系统实际上是处于正常条件下,而造成了不必要的停车,会引起重大的停车损失和潜在的安全问题。因此,危险失效和误跳车都会对安全和经济造成影响。研究表明,虽然停车/重启仅占整个运行时间的4%,但是25%的事故发生在停车和重启阶段[3]。另外根据 Exida公司对世界各地安全联锁系统统计的相关数据表明,误跳车是当前影响经济效益的关键因素之一[4]。

一般情况下,安全联锁系统 PFDavg的计算方法主要有两种,即故障树分析方法和马尔科夫模型。与针对 PFDavg的研究[5]相比,目前为止针对M T TFs的研究仍十分缺乏,M T TFs的计算始终是SIS评估中的瓶颈。研究表明,M TTFs计算主要存在两个问题:

a)根据典型的可靠性理论,在系统的寿命评估中,一般认为系统是不可修复的,而大多数安全联锁系统实际上是可以修复的(在线或者周期性地修复),并且修复对系统可靠性的影响非常大[6]。

b)在当前的 M T T Fs研究中,系统中元件的危险失效,包括可检测和不可检测危险失效,对M T T Fs的影响通常不予考虑,而在大多数情况下危险失效对M T T Fs的影响是确实存在的[7-8]。

在功能安全标准IEC 61511和ISAS 84.00.02-2002颁布以来,M T T Fs开始作为安全联锁系统评估的重要指标,已越来越受到业界关注。但十分遗憾的是,上述标准中没有提供M T T Fs的具体计算方法。随着诊断、检测技术的迅速发展,在线修复和维修已受到越来越广泛的关注,危险失效和修复对系统可靠性影响的研究需求变得越来越紧迫[9-10]。该文基于马尔科夫模型研究了“二取二”结构M T T Fs计算方法,深入分析了危险失效、在线修复及共因失效等因素对误跳车的影响。

1 “二取二”结构的马尔科夫模型及计算方法

1.1 基于经典马尔科夫模型的M T T Fs计算

经典马尔科夫模型如图1所示,在该模型里,有6个独立状态,每个状态的可靠性能相互转移。状态0(O K,正常)代表初始状态,即所有单元能正常工作并且可被完全检测。状态1和2是降级(Degraded)状态,即至少有一种失效发生,但是系统仍然维持预设功能。状态1和2的失效模式分别是降级的可检测和不可检测。状态3(Fail Safe, FS)代表安全失效状态,即系统发生误跳车。状态4(Fail Dangerous Detected,FDD)和 5(Fail Dangerous Undetected,FDU)分别表示危险可检测和危险不可检测失效状态,这两种状态均表示不能完成所要求的功能。

图1 经典“二取二”结构马尔科夫模型

依据经典的可靠性分析理论,即认为失效是不可修复且不可检测的,此时,系统的平均无故障工作时间计算如下:

方法一:针对具有吸收状态的马尔可夫模型, Control System Safety Evaluation and Reliability一书中,依据Laplace变换原理,采用矩阵变换的方法求解M T T F。但是该方法求解得到的是平均无故障工作时间 (M T T F),并非误跳车的指标M T T Fs,并且该方法未能充分考虑危险失效与维修对M T T F的影响。

方法二:根据文献[11]中介绍的求解马尔科夫模型M T T F的方法,得到M T T Fs的公式为:

式中 Rs(t)——安全失效概率。

经过推导求解[10],得出

式中 λABC中的“A”表示失效模式(“S”表示安全失效,“D”表示危险失效),“B”代表检测性(“D”表示可检测,“U”代表不可检测),“C”表示共因失效(“N”表示正常失效);μo——在线修复的修复率;T0,T1,T2——系统处在状态0,1,2的时间。

上述两种方法,只考虑安全失效对系统误跳车的影响,未充分考虑危险失效、失效检测性、维修等对误跳车的影响,因而在绝大多数情况下并不能反映误跳车的实际情况。针对上述不足,该文对经典Markov模型进行改进,进而在改进模型的基础上提出新的M T T Fs计算方法,该方法能够充分考虑危险失效、在线修复、共因失效的作用。

1.2 改进的“二取二”结构马尔科夫模型及计算

依据经典的可靠性理论观点,在马尔科夫模型中仅仅有一个吸收态5。而在改进的马尔科夫模型中,状态3为惟一吸收态[12]。改进后的马尔科夫模型如图2所示,图中μPTI表示周期性修复的修复率,其余符号与经典马尔科夫模型中符号意义相同。在改进的模型中主要考虑以下因素:

a)改进后的马尔科夫模型,客观上除了状态3都属于非误跳车状态。但是从可靠性观点看,危险失效状态(状态4和5)不能完成预设功能应该认为是不可靠的。从这个观点出发,系统处在危险失效状态的情形不应该包含在M T T Fs计算中。

b)另一方面,如果危险失效可通过在线检测或者周期性检查检测到并且确定,系统有机会进行修复并且恢复到正常状态。在这种情况下,危险失效影响了系统处于每个状态的概率,因此计算M T T Fs应充分考虑危险失效和维修的影响。

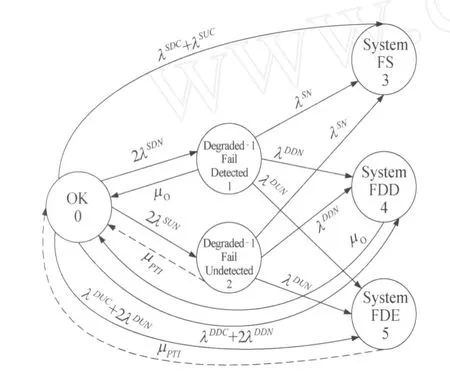
图2 改进后“二取二”结构马尔科夫模型

综合以上,在改进的模型中将危险失效状态作为非吸收态,但是考虑了危险失效和维修的作用。那么根据改进的模型,误跳车计算方法3:

式中 P0,P1,P2——单位时间内,系统处于0, 1,2的概率。

近似计算时,也可以表示:

式中 T0i,T1i,T2i——以单位小时为时间间隔的条件下,在第i小时内,系统处于0,1,2状态内可能的时间。在计算系统处于0,1,2状态的时间时,考虑了危险失效和维修所引起的概率重新分配。

1.3 计算比较

分别用基于马尔科夫模型的“二取二”结构M T T Fs的三种计算方法,计算表1中的四组可靠性数据,计算结果见表1右侧所示。假设失效率服从指数分布,每个单元的失效率分为安全不可检测率(S U),安全可检测率(S D),危险不可检测率(DU),危险可检测率 (DD),共因失效因子CC F=3%,平均修复时间M T T R=8 h。

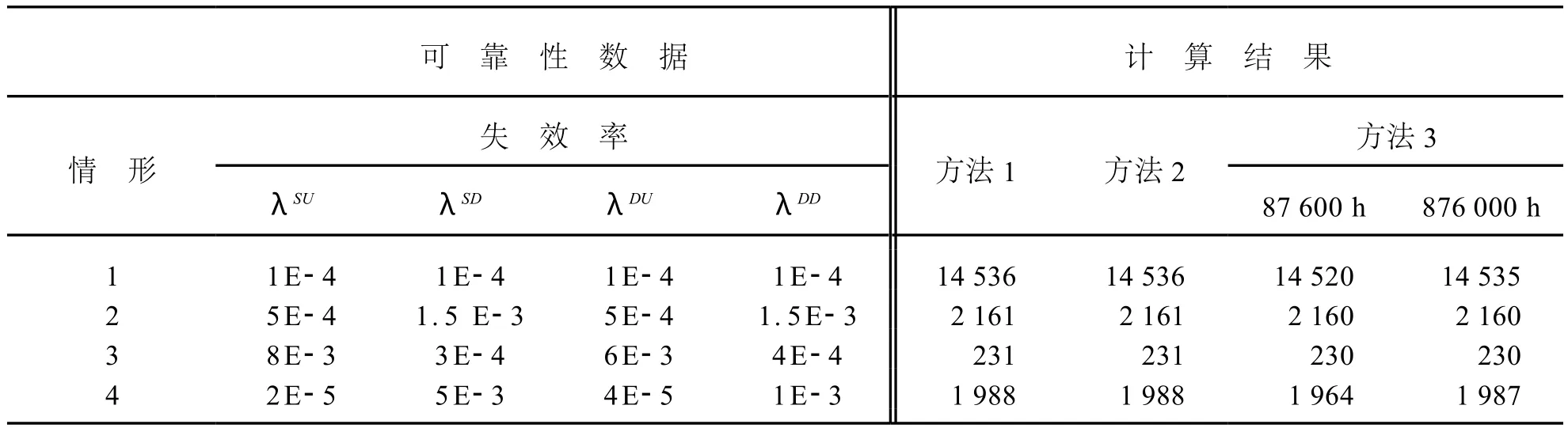
表1 可靠性数据和计算结果

从计算过程和表1的计算结果中,可以得出如下结论:

a)应用方法1时,只要按照马尔科夫模型状态转移图,写出转移矩阵,利用Excel电子表格即可进行求解。

b)应用方法2时,只要将可靠性数据代入等式,即可得出结果,方便可行,但是理论上当λS=0时,公式不可用。而在实际工程中,λS=0是不可能发生的。

c)方法1和方法2的结果完全一致。

d)方法3的计算结果与所选可靠性数据及计算次数有关;计算次数越多,计算结果与方法1,2所得结果越接近。此外,研究发现当失效率数据的数量级达到10-7时,计算次数将需要达到上千万次,系统非误跳车状态的概率才趋于0。

以上的结论说明,3种不同的计算方法,对于同一组数据得到相同的M T T Fs,验证了基于改进的马尔科夫模型提出的计算方法的正确性。至于前文提到的危险失效、在线修复对 M T T Fs的影响,只能采用方法3进行深入分析。

2 分析危险失效和在线修复对“二取二”结构M T TFs影响

2.1 危险失效对“二取二”结构M T T Fs的影响

失效作为状态的一种特殊类型,具有惟一性。这就意味着系统有且仅有一种确定的失效状态,安全失效或者危险失效。如果单元以危险方式失效,那么就不会发生安全失效,也就是说危险失效和安全失效是互斥的。对于危险失效,如果没有采用修复策略,那么失效单元不可能恢复。而如果采用适当修复策略,并且使得系统“修旧如新”,则危险失效对系统误跳车产生一定的影响。

为了评估危险失效对系统可靠性的影响,分别研究了表2中六种不同的情形,在危险失效率不断增加的情况下M T T Fs的变化情况。

表2 六种不同情形可靠性数据

从以上比较可以发现,危险失效的存在对M T T Fs有着复杂的影响。可以归结为:

a)在六种情形中,随着危险失效率的增加, M T T Fs的总趋势是增加的。在某种程度上说,危险失效的存在实际上降低了系统的误跳车,如图3所示。

图3 危险失效率对M T T Fs影响

b)危险可检测失效与危险不可检测失效对M T T Fs影响相同(Case 1&Case 4对比),总体上M T T Fs随危险失效数据的增加而增加,但是增加的绝对数量很小,如图4所示。

c)使用维修策略,且安全可修复失效存在(不为零)时,维修实际上可大大降低误跳车(Case 1& Case 5对比)。

d)使用维修策略,但可修复的安全失效很小(为零)时,维修对降低误跳车的效果不明显(Case 3&Case 6对比)。

e)不进行维修时,危险失效的增加对M T T Fs的影响非常大,不可忽略;此外,危险可检测失效的存在实际上有助于降低误跳车,但效果不明显(Case 5&Case 6对比),如图5所示。

2.2 在线修复对“二取二”结构M T T Fs的影响

根据传统的可靠性理论,在M T T Fs计算过程中认为系统是不可修复的,但是这并不意味着修复对系统可靠性没有影响。根据在线修复定义,意味着一旦单元/系统检测到危险,就立刻修复,但是这仅仅对可检测失效有用。

关于在线修复对M TTFs的影响,该文针对五种情形下的五种不同修复策略进行研究。表3列出了五种不同情形的M TTFs。在这里假设所检测到的失效都能完全修复,并且使得系统“修旧如新”。

从表3中,可以看出五种情形中,在线修复对M T T Fs影响的整体趋势:随着在线修复周期的增加,M TTFs逐渐减少。在1,2,3三种情形中,在线修复策略对 M T TFs的影响较小,基本可以忽略。但是在4,5两种情形中,在线修复对 M T TFs的影响值得注意,可以通过降低在线修复周期来提高M T TFs,即提高在线维修的速度可降低误跳车。

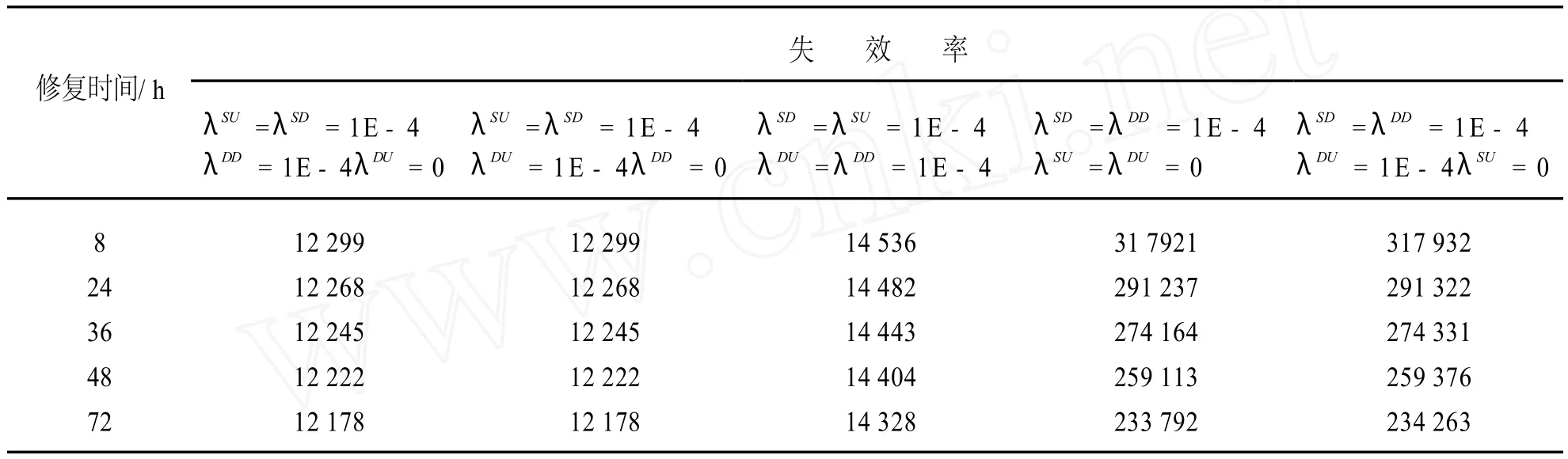
表3 在线修复对M TTFs影响

2.3 共因失效对“二取二”结构M T T Fs的影响

为了评估共因失效对“二取二”结构 M T T Fs的影响,文章研究了在λSU=λSD=1E-4的如下五种情形下,随着共因失效因子的增加,M T T Fs的变化情况。

表4 五种不同情形可靠性数据

从图6中可以看出,当λD≤λS时,共因失效对M T T Fs的影响基本可以忽略;当λD＞λS,共因失效因子的增大,会使得M T T Fs逐渐减小。并且随着危险失效的增加,共因失效因子对M T T Fs的影响逐渐增大。共因失效对 M T T Fs的影响整体趋势:随着共因失效因子的增加,M T T Fs逐渐减小。因此在工程实际中,选择系统单元要充分考虑共因失效的影响,通过对冗余单元进行物理隔离,保证单元多样性,强化设计提高单元强度等方法来避免共因失效。

3 结束语

文章验证了基于改进马尔科夫模型提出的M T T Fs计算方法的正确性,并利用此计算方法深入分析了危险失效、维修、共因失效对“二取二”结构误跳车的影响,具体结论如下:

a)三种基于马尔科夫模型的“二取二”结构M T T Fs计算结果基本一致。方法1和2结果完全一致,方法2所推导出来的公式,在计算时直接代入可靠性数据即可获得,十分便捷。方法3在计算M T TFs时,能够充分考虑危险失效和在线修复对M T TFs的影响,更能真实反映误跳车的实际情况。

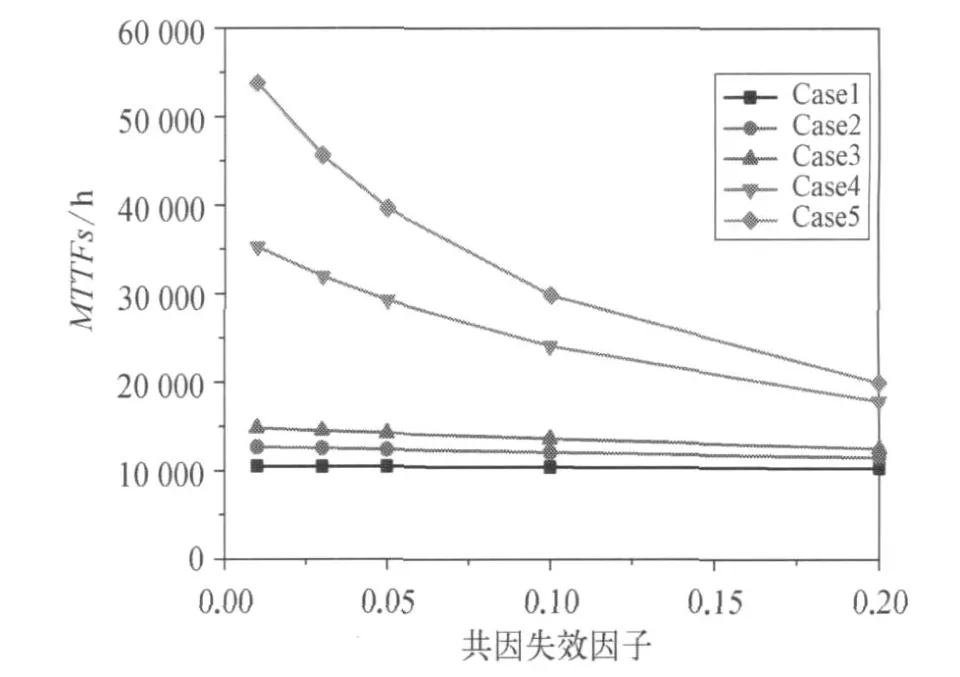
图6 共因失效因子与M T T Fs关系

b)随着危险失效率的增加,M T T Fs的总趋势是增加的。在某种程度上说,危险失效事实上是对非误跳车有利的。

c)随着在线修复率的增加,M T T Fs整体趋势是逐渐增加,这就意味着在线修复是一种很好的降低误跳车的措施。

d)随着共因失效因子的增加,M T T Fs整体趋势是逐渐减小,因此降低共因失效也是一种很好的降低误跳车的措施。

[1] IEC 61511-1 Functional Safety-Safety Instrumented Systems for the Process Industry Sector-Part1:Framework, Definitions,System,Hardware and Software Requirements [S].International Electrotechnical Commission,2003.

[2] ISA S84.00.01 FunctionalSafety:Safety Instrumented Systems for the Process Industry Sector-Part1:Framework, Definitions,System,Hardware and Software Requirements [S].Instrument Society of America,2004.

[3] REASON J T.Managingthe Risks ofOrganizational Accidents[M].Ashgate,1997.

[4] MILLER C.Win-Win:A Manager's Guide to Functional Safety[M].Exida,2008.

[5] 周 华,左 信,郑加平.安全仪表系统可靠性影响参数的敏感性分析[J].化工自动化及表,2010,37(3):66-68.

[6] GOBLE W M.Control System Reliability &Evaluation [M].ISA-The Instrumentation,Systems,and Automation Society,1998.

[7] BU KOWSKI J V,GOBL E W M.Defining Mean Timeto-Failure in a Particular Failure-State for Multi-Failure-State Systems[J].IEEE Transactions on Reliability,2000 (50):221-228.

[8] BU KOWSKI J V.Modeling and Analyzing the Effects of Periodic Inspection on the Performance of Safety-Critical Systems[J].IEEE Transactions on Reliability,2001(50): 321-329.

[9] ZHU J X,WANG L J.A method for the Calculation of the Mean Time to Failure(MTTF)of Repairable System[J]. Advanced Materials Research,2008,(44-46):813-819.

[10] ZHU J X,WANG L J,GAO Z L,et al.Calculation of Safety and Spurious Trip of Safety Instrumented System Based on Failure Mode[J].Pressure Vessel Technology, 2007,(7):12-16.

[11] SMITH D J.Reliability,Maintainability and Risk:Practical Methods for Engineers [M]. 7th. Butterworth-Heinemann,2005.

[12] ZHU J X,CHEN X D,BAO S Y,et al.Research on Spurious Trip of 1oo2 Safety Instruments of Petrochemical Installation with Repair Considered[J].Advanced Materials Research,2010,118:596-600.