双程声波方程逆时深度偏移
2010-01-12何兵寿张会星范国苗
何兵寿,张会星,范国苗
(中国海洋大学 海底科学与探测技术教育部重点实验室,山东青岛 266100)
0 前言
地震波偏移是地震勘探领域的核心技术,工业界对地震波场叠前偏移的要求主要有二方面:
(1)复杂构造的精确成像。
(2)提供叠前反演所需的道集。
在理论上,基于双程波方程的地震资料,叠前逆时深度偏移技术能够同时达到以上目标,因此该项技术在提出之初就展现出良好的工业应用前景。近年来,随着油气生产对地震勘探精度要求的不断提高,勘探目标构造与岩性复杂程度的不断增加,业界开始逐渐研究并采用实用的地震波叠前逆时深度偏移技术来解决问题,以达到提高勘探精度与实现岩性勘探等目标。
多年来,国内、外地球物理学者在逆时偏移领域进行了大量的研究工作,并取得了许多成果[1~5]。但目前为止,基于双程波方程的逆时偏移技术在工业生产资料的实际应用方面还少有成功实例,限制该项技术进入工业应用领域的主要原因在于:
(1)地震波方程逆时延拓本身还有许多技术问题需要进一步完善,如计算精度的进一步提高,截断边界伪反射的压制等。
(2)双程波方程逆时偏移的成像准则与成像条件的计算方法需进一步深入研究,在地震波方程逆时延拓过程中,地下各点在何时成像,如何成像是决定偏移效果的又一关键因素。而目前常用的,基于时间一致性准则的激发时间成像条件,无法补偿地震波逆时延拓过程中的层间能量反射损失,难以达到理想的偏移效果。
(3)在双程波方程逆时延拓过程中产生的层间反射干扰,需要新的方法来压制,逆时偏移中的层间反射会使浅层产生强振幅干扰,恶化剖面浅层部份的成像结果。
作者在本文引入了波动方程正演中的交错网格高阶差分技术[6]和最佳匹配层边界吸收技术[7],以提高声波方程逆时延拓的精度。对于叠后逆时偏移,作者采用了基于爆炸反射界面的零时间成像条件进行波场成像。对于叠前逆时深度偏移,应用上行、下行波归一化互相关成像条件,压制了部份层间反射,并补偿了深层能量,最终实现了声波方程的逆时偏移。
1 双程声波方程的逆时延拓算法
1.1 双程声波方程逆时延拓的高阶差分格式
在二维情况下,各向同性介质中的双程声波方程为:
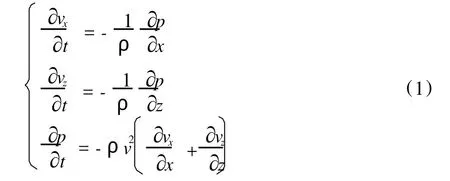
其中 vx、vz分别为质点在x与z方向的振动速度,p为位移;v为纵波速度;ρ为密度;x、z分别为空间坐标;t为时间。
借鉴一阶声波方程的正演方法算法,在图1所示的交错网格空间中,对式(1)进行高阶差分离散,可得反射纵波逆时延拓的高阶差分格式:
其中:Δx、Δz分别为x与z方向的空间离散步长;Δt为时间离散步长;N为差分阶数的一半;i、j为空间离散点序号;n为时间离散点序号;为差分系数,其值详见参考文献[6]。
以地面记录作为边值条件,利用式(2)即可求解地震波的逆时传播问题。
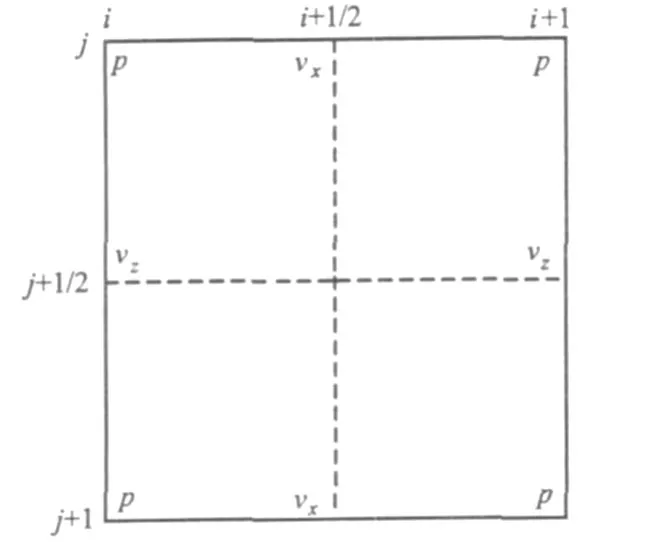
图1 交错网格示意图Fig.1 The diagram staggered grids
1.2 稳定性条件与吸收边界条件
经推导,式(2)~式(4)的稳定性条件为:
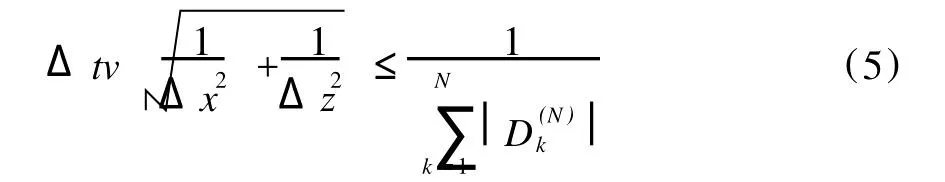
采用最佳匹配层(PML)吸收边界条件,解决截断边界的伪反射问题。依据PML的方程分裂思路[7],可得:
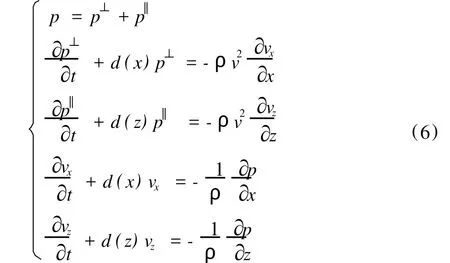
其中 p⊥和p‖分别为p分量在x与z方向的分裂算子;d(x)和d(z)分别为x和z方向的衰减因子。对于左边界和右边界,有d(z)=0;对于上边界和下边界,有d(x)=0。
同样在交错网格空间中对式(4)进行差分离散,可得到适用于双程声波方程逆时偏移的PML边界差分格式,详细推导过程这里不再赘述。
2 双程声波方程逆时偏移的成像条件
2.1 叠后逆时偏移的成像条件
叠后反射纵波剖面可等效为在各岩性分界面上,以不同强度同时激发的地震波,以速度v/2(v为地层速度)传播至地表并被记录的结果,这就是目前叠后偏移中常用的爆炸反射界面原理。这一原理同样对声波方程的叠后逆时偏移有效,故叠后逆时偏移的成像条件为:其中 I mage(x,z)为对应网格点的偏移成像结果;为接收点记录逆时延拓至t=0时刻地下各点的波场值;x,z为空间坐标。

2.2 叠前逆时偏移的成像条件
在纵波方程的叠前逆时深度偏移领域,Claerbout[8]提出的上行、下行波互相关成像条件可概括为:其中 I mage(x,z)为对应网格点的偏移成像结果;为接收点记录逆时延拓波场值;x、z为空间坐标;tmax为记录长度;为炮点子波正向延拓波场值。
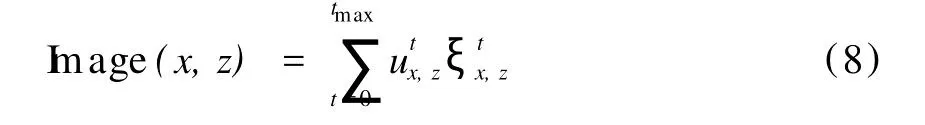
式(8)实质上是炮点正向延拓波场与检波点逆时延拓波场的互相关运算,对于深部地层来说,由于在检波点波场逆时延拓过程中,同样存在能量的衰减,但这种衰减不是由介质的弹性参数所引起,而是由逆时延拓算法本身引起的,其本质是一种误差,且深度越大,这种误差对偏移结果的影响也越大。为克服这一局限,可利用炮点波场值对式(8)进行归一,得到新的成像条件:
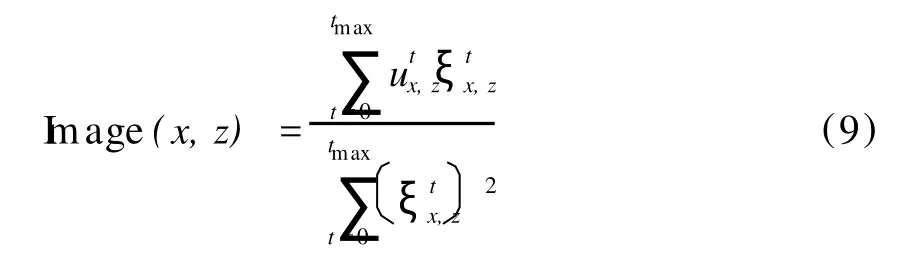
式(9)中的分母项与地震波正向传播过程中的能量损失有关,能量损失越大,其值越大。因此,式(9)对深层地震波能量有较强的补偿作用,便于深部地层的成像,作者在本文采用这种归一化的互相关成像条件,来实现双程声波方程的叠前逆时深度偏移。
3 双程声波方程逆时偏移的脉冲响应
3.1 均匀介质中的脉冲响应
如图2所示,脉冲主频为50 Hz且各脉冲能量相同,均匀介质模型的纵波速度为3 000 m/s。

图2 脉冲响应试验数据Fig.2 seismic data for impulse response test
图3(a)为采用式(8)得到的双程声波方程逆时偏移的脉冲响应,此脉冲响应表明双程声波方程逆时偏移技术,具有良好的倾角适应性。由于双程声波方程在推导过程中未做任何倾角假设,故以其为理论基础的逆时偏移算法,可对任意倾角的地层进行成像。通过分析图3(a)也可得到互相关成像条件的主要缺陷,表现为:深层成像结果中地震波振幅衰减严重,且其衰减机理与地震波正向传播时的衰减机理相同。而事实上,震源激发的地震波,在下行传播至反射界面过程中会产生能量衰减。当下行波遇到反射界面后,产生的反射波在上行至地表接收点的过程中,也会产生能量的衰减,其衰减程度与波的传播路径和所经过介质的弹性性质有关。这说明,对于地表接收到的一次反射波来说,地震波传播过程中能量的衰减必然发生二次(上行一次,下行一次),也只会发生二次。而利用双程声波方程进行逆时延拓时,地震波的能量就会产生第三次衰减,这显然与一次反射波的传播机理相悖。同时,地震波逆时偏移的目标,是将来自地下各反射点的一次反射波在成像时刻,全部聚焦到对应的反射点位置处,这就要求接收点波场在逆时延拓过程中不会产生能量的损失,而基于求解双程波方程的逆时延拓算法是无法做到这一点的。
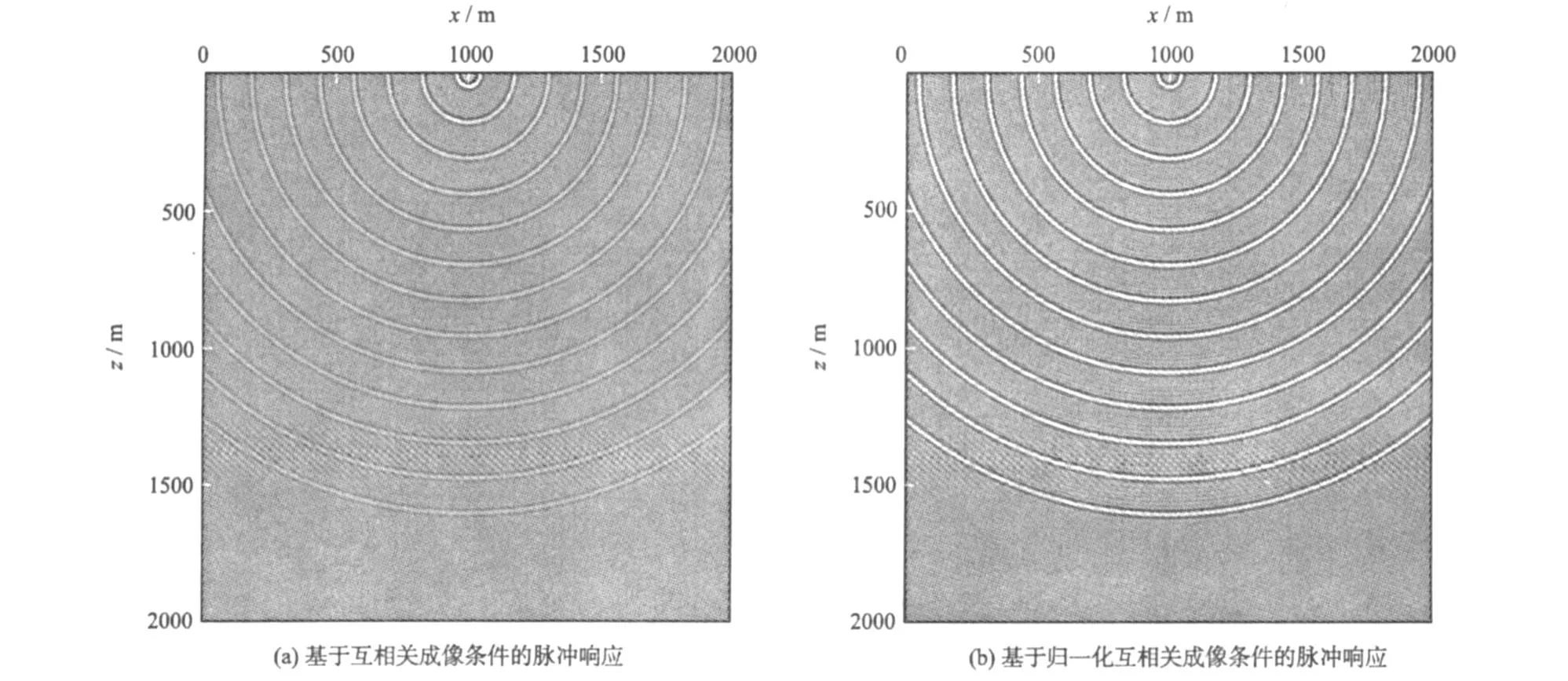
图3 均匀介质中双程声波方程逆时偏移的脉冲响应Fig.3 Reverse-time migration impulse response of two-way acoustic equation in homogeneous media
作者在本文采用式(9)作为逆时偏移的成像条件,以部份补偿地震波在逆时延拓过程中发生的第三次能量损失。图3(b)为基于归一化互相关成像条件得到的脉冲响应。分析对比图3(a)与图3(b),可以得以下结论:
(1)在二种成像条件下,各波组内部各道的能量关系未发生变化,这表明式(9)未改变逆时偏移中各成像点地震波动力学特征的相对关系。
(2)在图3(b)中,各脉冲的响应在能量上保持一致,这表明算法补偿了地震波逆时延拓过程中的第三次能量衰减。在本例中,由于模型为均匀各向同性介质,此时能量的衰减只可能由地震波的几何扩散引起,说明在均匀介质情况下,式(9)可补偿地震波在逆时延拓过程中,由于球面扩散造成的地震波能量衰减。因此,归一化互相关成像条件更有利于深部地层的成像。在复杂模型条件下,由各种因素所造成能量衰减的补偿方法,是今后逆时偏移领域的研究重点。作者在本文后续的叠前偏移算例中,均以式(9)作为成像条件。
3.2 层状介质中的脉冲响应
研究均匀介质情况下的偏移脉冲响应只有理论意义,层状介质在油气勘探中最为常见,为分析问题方便,作者将在本文中研究水平层状介质的脉冲响应。假设地下共有四层介质,其速度分别为3 000 m/s、3 400 m/s、3 800 m/s、4 200 m/s;三个速度分界面埋深分别为500 m、1 000 m、1 500 m。图4是图2所示数据的叠前逆时深度偏移结果,脉冲响应同样显示出了逆时偏移良好的陡倾角适应性,但水平层状介质的逆时偏移脉冲响应,受到了层间反射的干扰(图4中箭头所指处)。层间反射是由检波点波场逆时延拓过程中在速度分界面处产生的反射波所引起的,其本质是一种偏移噪声,在偏移结果中主要表现为近地表处出现许多低频强振幅干扰。目前,地球物理学界针对逆时偏移中层间反射的压制问题,进行了许多研究工作[9~12],取得了一些成果,但该问题的根本解决还需要结合逆时偏移算法本身,或采用单程波方程来实现。有关层间反射的详细压制方法,作者暂不讨论。
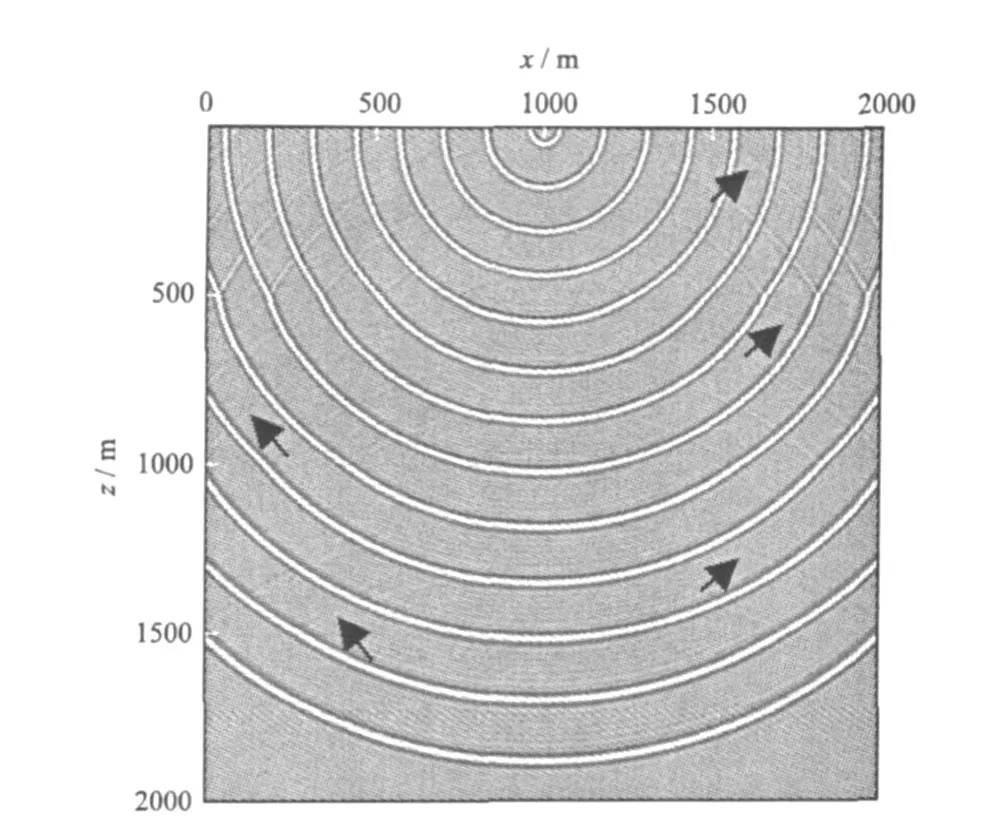
图4 水平层状介质中双程声波方程逆时偏移的脉冲响应Fig.4 Reverse-time migration impulse response of acoustic equation in horizontally layered elastic medium
3.3 连续速度介质中的脉冲响应
连续介质的速度为:

式中 z为深度。
图5是在该模型条件下的双程声波方程逆时偏移脉冲响应。由图5可见,在连续速度介质中,逆时偏移层间反射干扰远低于存在较大速度分界面的层状介质情况,这是由于连续速度介质中不存在大的波阻抗差,层间反射波的能量极弱所致。这说明对存在明显速度分界面的层速度模型进行适当平滑,可压制层间反射干扰。

图5 连续速度介质中双程声波方程逆时偏移的脉冲响应Fig.5 Reverse-time migration impulse response of acoustic equation in continuous medium
4 模型算例
4.1 叠后逆时深度偏移模型算例
利用sigsbee_2b纵波速度模型(见图6),检验双程声波方程叠后逆时偏移对复杂构造的成像能力。该模型中存在一个高速异常体、一系列断层、二组绕射点(图6中虚箭头所指处)和若干套地层。在高速体上方8 km和12 km位置处,存在一些高速的零碎沉积物。叠后逆时偏移所用的零偏移距理论数据,可以通过有限差分求解波动方程获得,正演所用的震源为主频50 Hz的雷克子波。
图7为正演得到的零偏移距剖面。在图7中存在大量绕射波,各波组十分复杂,无法用此叠加剖面直接进行构造解释。
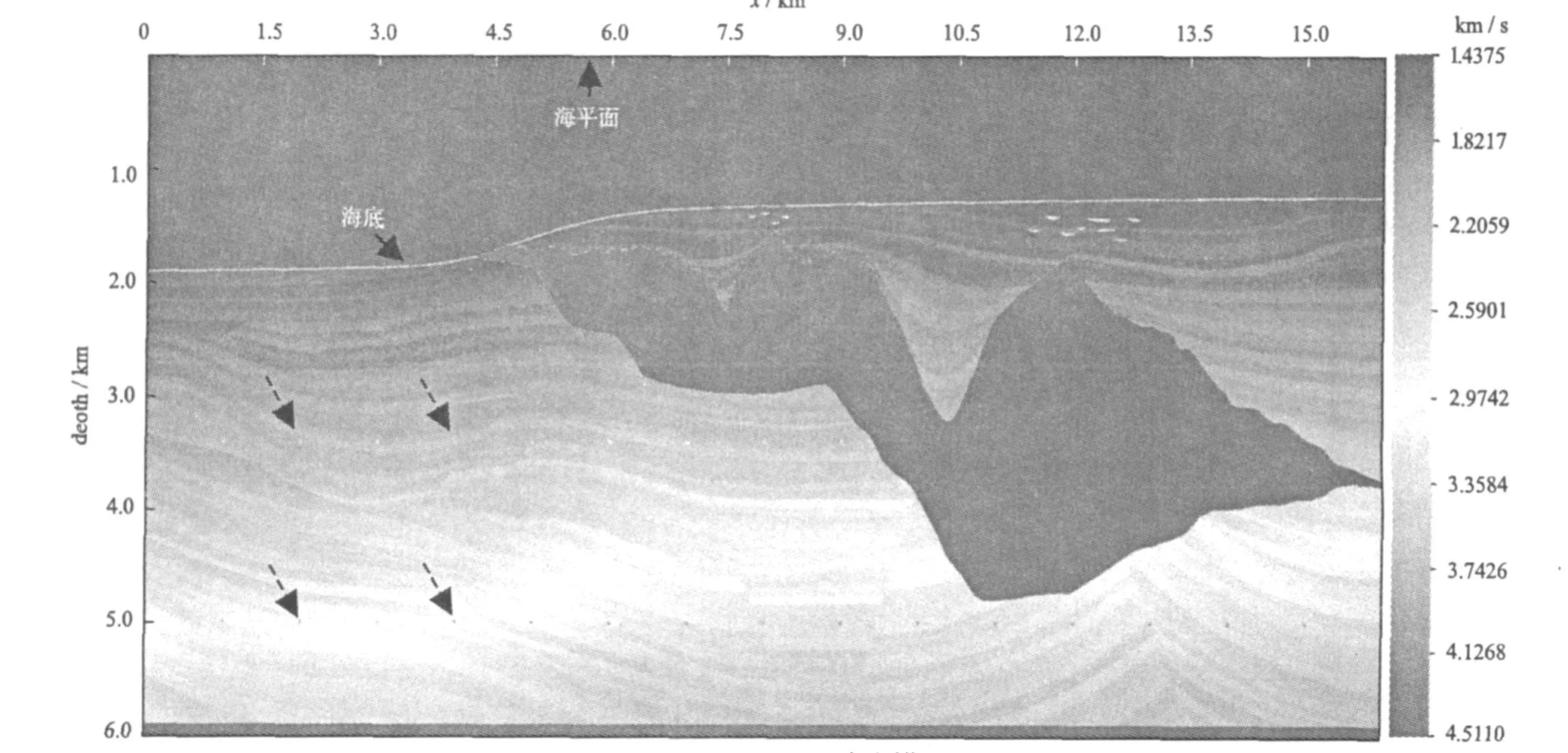
图6 sigsbee_2b速度模型Fig.6 Sigsbee_2b compression wave velocity model

图7 sigsbee_2b模型正演零偏移距剖面Fig.7 Zero offset seismogram of sigsbee_2b model

图8 图7的叠后逆时深度偏移结果Fig.8 Post stack reverse-time migration result of Fig.7
图8为采用本文的叠后逆时偏移方法得到的成像结果。在图8中,海底地形、高速体顶底界面、高速体上部地层和模型左部的地层均得到了很好的成像,但高速体底部地层由于受高速体屏蔽的影响难以准确成像,这是叠后偏移的局限,利用叠前逆时深度偏移技术可解决高速体下部地层的成像问题。
4.2 叠前逆时深度偏移算例
对sigsbee_2b模型的理论单炮数据进行叠前逆时深度偏移,单炮记录按以下观测系统,通过双程声波方程有限差分正演获得:纵波源激发,震源为主频50 Hz的雷克子波,中间放炮,炮点二侧共501道接收,测线二端固定排列不动,只移动炮点位置,道间距0.005 km,炮间距0.05 km,记录长度7.5 s,共得321炮合成记录。
图9(见下页)为各单炮记录叠前逆时深度偏移后的共成像点叠加剖面,高速体下部地层的成像质量得到的明显改善,说明基于双程声波方程的叠前逆时深度偏移算法,能够对复杂构造进行成像。
5 结论及展望
波动方程逆时偏移技术具有不受倾角限制与高保真性等优点,是解决复杂构造成像问题的理想工具。作者在本文推导的基于交错网格的双程声波方程高阶逆时延拓算子,与相应的PML吸收边界条件可实现地表波场的高精度逆时延拓。并且归一化互相关成像条件,可有效补偿地震波逆时延拓过程中的能量损失。综合应用这二项技术,可实现复杂构造的精确成像。
层间反射的压制技术与层速度建模技术,是波动方程逆时偏移领域的难点,目前的技术无法在不损伤有效信号的前提下完全去除层间反射干扰。层间反射的压制问题,已成为制约基于双程波方程的逆时偏移技术进入工业应用领域的主要因素之一。该问题的最终解决,将会有力推动逆时偏移技术进入工业化生产阶段,并进一步提高地震资料成像处理的精度。层速度建模方面,在不考虑地层各向异性的前提下,逆时偏移所需的层速度,可参考其它叠前深度偏移技术的建模方法,并综合利用地质、测井,及其它已知资料来获得。更为精确的速度建模技术,需要针对逆时偏移算法本身的特点来研究。除相关理论与方法需进一步完善外,巨大的计算量也是限制逆时偏移技术进入工业应用领域的一大障碍。但随着计算机硬件的高速发展,特别是微机群的普及与GPU的推广,逆时偏移技术必将在未来的油气勘探中发挥巨大作用。

图9 Sigsbee_2b模型的叠前逆时深度偏移结果Fig.9 Pre-stack reverse-time migration stack profile of sigsbee_2b data
[1] WHITEMORE N D.Iterative depth migration by backward time propagation[C].Expanded Abstracts of 53rdSEG Annual Int Mtg,1983.
[2] MCMECHAN GA.Migration by extrapolation of timedependent boundary values[J].Geophysical Prospecting,1983,31(2):413.
[3] CHATTOPADHYAY S,MCMECHANG A. Imaging conditions for prestack reverse-time migration[J].Geophysics,2008,73(3):S81.
[4] STEVE T H.Reverse-t ime depth migration: Impedance imaging condition[J].Geophysics,1987,52(8):1060.
[5] SCHLEI CHER J,COSTA J C.A comparison of imaging conditions for wave-equation shot-profile migration[J].Geophysics,2008,73(6):S219.
[6] 董良国,马在田,曹景忠,等.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,2000,43(3):411.
[7] BERFENGER J P.A perfectly matched layer for the absorption of electro magnetics waves[J].Journal Computation Physics,1994,114(2):185.
[8] CLAERBOUT J F.Toward a unified theory of reflector mapping[J].Geophysics,1971,36(3):467.
[9] FLETCHER R P,FOWLER P J,KITCHENS IDE P,et al.Suppressing unwanted internal reflections in prestack reverse-time migration[J].Geophysics,2006,71(6):E79.
[10]YOON K,MARFURT K J.Revsrse-time migration using the pointing vector[J].Exploration Geophysics,2006,59(1):102.
[11]GUITTON A,KAELIN B.Least-square attenuation of reverse time migration artifacts[C].Expanded Abstracts of 76rdSEG Annual Int Mtg,2006:2348.
[12]GUITTON A,VALENCIANO A,BEVC D,et al.Smoothing imaging condition for shot-profile migration[J].Geophysics,2007,72(3):S149.
