基于二元树复小波和SVD不变性的纹理图像分类算法

黄荣兵,苏长明,郎方年

(成都大学信息科学与技术学院,四川成都 610106)

0 引 言

纹理是反映图像的重要视觉特征之一,它广泛存在于各类图像中,通过对纹理图像进行分析可获得许多有用的信息.纹理分析在基于内容的图像检索、目标识别、医学图像分析等应用领域有着巨大的影响,而纹理分类又是纹理分析中最重要的方面.要进行纹理分类,纹理特征的提取和分类器的设计是决定分类正确率的关键.目前,纹理特征提取的方法主要有统计法、结构法、模型法和空间/频域分析法4类.采用具有空间/频域分析能力的小波变换对纹理特征进行提取和分析方法是常用的手段并已取得了一定的成果[1].最常用的小波变换是基于Mallat的金字塔算法,虽然其优点突出,但它的时移敏感性影响了其应用.为了克服这个缺点,研究者提出了不同的解决方案[2].文献[3]提出了利用正交小波变换提取图像纹理特征的算法,该算法虽然具有分析不同尺度纹理的特性,但仍存在两点不足:①不具备平移不变性,即输入图像很小的位移可能会造成不同尺度的离散小波变换(DWT)系数之间能量分布很大的变化;②由于小波滤波器是实数域的离散滤波器,使得这种纹理分析法不具备对角线方向的选择性.此外,Gabor函数能够很好地模拟人类视觉感受,最佳地描述时频域的局部特性,可达到空间域和频域联合测不准下限.将Gabor函数进行旋转和尺度变换构造的Gabor滤波器组可用来提取多尺度的图像信息,但用该方法得到的特征向量维数过高,计算量太大,并产生较多的冗余信息[4].

另外,近年来有学者提出的双树复数小波变换(Dual-tree Complex Wavelet Transform,DT-CWT)[5]不仅具有DWT的诸多优点,还具有近似平移不变性和很好的方向选择性,且能对图像进行很好的重构,并已广泛应用于图像分析和模识别中[6,7].虽然该方法能够很好地刻画图像的纹理特性,但它敏感于旋转和尺度等几何变换.而SVD作为一种代数特征方法却具有旋转和尺度不变性等优点.因此,本文结合DT-CWT和SVD各自的优点,提出一种有效的纹理图像分类算法.

1 双树复小波变换

DT-CWT具有与经典的Gabor小波变换相似的特性,但它的冗余度远小于Gabor小波变换的冗余度,其结构如图1所示.为了使得DT-CWT具备近似平移不变性,可对树状结构的每一层滤波器的输出做因子为2的下采样.

从图1中可以看出,DT-CWT由两棵平行的小波树构成,并且每棵树又由奇、偶交替的正交分解低通滤波器和高通滤波器组成,分别记为:H0(Z)和H1(Z)= Z-1H0(- Z-1),(Z= e2πiω).令,

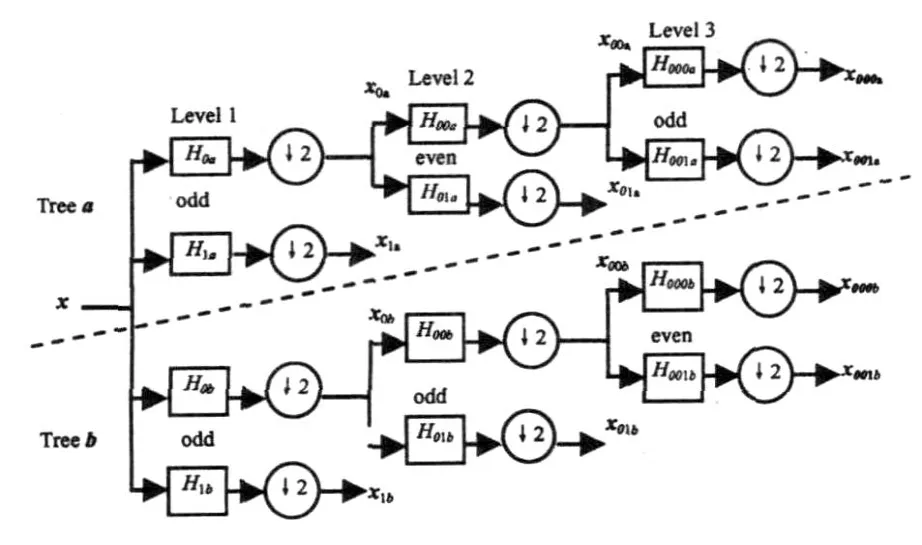
图1 1-D双树复小波变换滤波器结构示意图

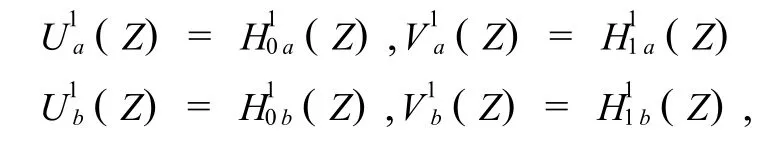
当 j=1,2,…,n(n是分解层数)时,令,

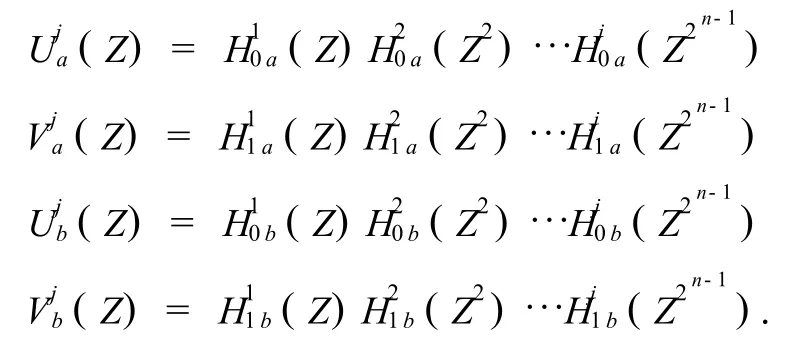
则一维信号S(Z)在第n层的DT-CWT分解结果为,

其中,(2j↓)表示以2j向下采样,下标a/b分别对应±,Cj和Dj分别为低频和高频系数.

通过对图像的行和列分别进行DT-CWT滤波,即对列滤波器的输出再进行行滤波器复共轭滤波,可把1-D DT-CWT扩展到2-D,则此时在第n层二维信号S(Z1,Z2)的DT-CWT分解结果为,

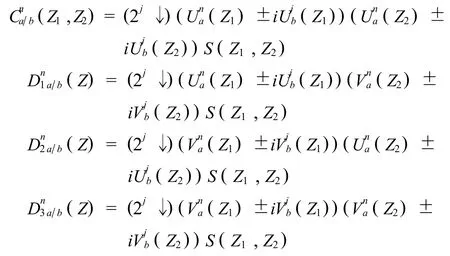
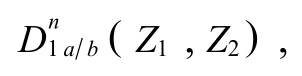
图2 (a)二维双树复小波变换的实部,(b)二维离散小波变换

图3 Lena图像的DT-CWT一级纹理分解的实部

2 奇异值分解

奇异值分解是一种有效的代数特征提取方法.由于奇异值特征在描述图像数值上比较稳定且有旋转不变、位移不变、比例不变性等重要性质[8],常作为图像分析中的一种有效的特征描述工具[9].

设矩阵C是一个N×M维的实矩阵,其秩为r,则存在正交矩阵U(N×N维),V(M×M维)和对角线矩阵Λ(N×M维)满足,

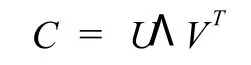
式中,Λ=diag(λ1,λ2,…,λr,0,0,…,0).λ1到λr是矩阵C的奇异值,也就是矩阵CC′的特征值.U和V分别为矩阵C的左右奇异值矩阵.

设,λ1≥λ2≥…λr＞0,令,∑=(λ1,λ2,…, λr).由于矩阵的奇异值具有与其行列位置的无关性,即当矩阵的行顺序发生交换时,奇异值仍将保持不变.由于特征矩阵满足平移和比例不变性,故这里∑就是具有3个不变性的图像的特征向量.

3 分类器及算法实现

3.1 BP神经网络学习算法

BP神经网络由大量神经元互联而成,其结构简单、算法成熟,且具有较强的适应和学习能力,利用BP神经网络进行模式分析是近年来在该领域研究的一个重点[10].BP算法是非循环多级网络的训练算法,其学习过程主要由正向传播和反向传播组成,输入值经过非线性变换从输入层经隐层单元逐层处理,并传向输出层,每一层神经元的状态将影响到下一层神经元状态,如果在输出层不能得到期望的输出,则转入反向传播,通过修改各神经元权值,从而使误差信号最小.

3.2 改进的BP算法

虽然BP算法是目前应用最为普遍的一种神经网络训练学习方法,但在实际应用中却出现了两个突出的问题:收敛速度慢与可能收敛到局部极小点.对此,国内外许多研究者做了大量的工作,比如:为了加快BP算法的收敛速度,可在标准BP算法的基础上采取动态调整确定学习步幅、自适应改变惯性系数等措施;为了克服局部极小,通过采用其他的优化方法如模拟退火法、遗传算法等来改进BP算法,以求能够找到全局最优解.

遗传算法(Genetic Algorithm,简称G A)采用启发式搜索技术寻找最优解,与传统优化方法相比,具有搜索效率高、鲁棒性好、对目标函数限制少、采用并行运算等特点[10].本文将遗传算法引入BP网络学习中,形成一种遗传BP算法(Genetic-Backpropagation Algorithm,简称G BPA).此算法将 G A的全局寻优能力与BP算法的指导搜索思想结合起来,既克服了寻优中的盲目性,又避免了收敛到局部极小点的情况的发生.遗传BP算法的具体步聚如下:

(1)首先凭经验确定BP神经网络各连接权值的实数范围,然后根据问题所要求的精度确定各权值的编码长度.

(2)在所获得的编码的解空间中,随机产生一组具有M个个体的初始种群,X=(X1,X2,…,Xm)T,种群中每个个体,Xi=(X1,X2,…,Xn),代表一个神经网络的初始权值分布,每个基因值表示一个神经网络的一个连接权值,个体的长度为神经网络权值的个数,则最后产生M组初始网络权值.

(3)用BP算法对这M组初始权值进行训练,如果经过训练后这M组权值中至少有一组满足精度要求,则算法转至步聚(7);否则转入步聚(4).

(4)依据经过训练的上述 M组网络权值,再随机产生一组具有R个个体的种群,同时生成R组新的权值,最终和经过训练的M组权值一起,构成完整的基因群体,共有M+R组权值.

(5)对这 M+R组权值进行选择(selection)、交叉(crossover)、变异(mutation)遗传操作.

(6)如果经过步聚(5)的操作已经至少得到一组符合精度要求的权值,则算法转至步聚(7);否则从经过遗传操作的和未经过遗传操作的这2＊(R+ M)组权值中选出M组较好的权值,返回步聚(3).

(7)取在整个遗传操作中得到的最优个体作为神经网络的初始权值,然后再利用BP算法对神经网络进行训练,求得最优解.

为了判断权值是否满足精度要求的标准,我们选用该组权值对应的网络的相对均方误差 Erms,即

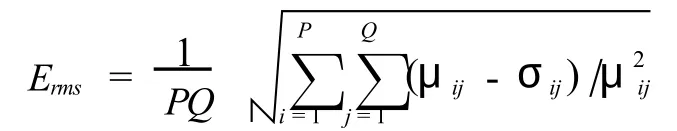
其中,P是训练样本数;Q是网络输出矢量的维数; μij是期望的输出值;σij是实际的输出值.

至此,给出本文所提出算法的整个步聚如下:

步聚1 对纹理图像进行预处理,通过高斯滤波对其进行平滑处理去除噪声.

步聚2 进行三级2D DT-CWT分解,每一级可获得6个细节子带的幅值图像,从而得到18幅子带图像,即18个矩阵.

步聚3 对第二步所获得的18个矩阵进行SVD分解,得到18个对角矩阵,∑1,∑2,…,∑18.令∑m=(λm1,λm2,λmr),m=1,2,…,18,则可以得到一个 m×r维的特征矢量,Iλ=(λ12,λ12,…,λ1r,λ21, λ22,…,λ2r,…,λ181,…,λ18r).

步聚5 设计BP网络分类器,并将特征矢量输入网络进行训练.

步聚6 对拟测试的纹理图像按照步聚1～4获得纹理特征,然后输入BP网络,最后得到分类结果.

4 实验结果与分析

为检验本文所提出算法的有效性,我们选用了Brodatz[11]纹理库中的纹理图像,部分实验纹理图像如图4示.另外,为验证几何不变性,人为地对某些图像进行了旋转和缩放等操作之后,放入纹理库中进行训练和测试.图4(a)为库中的原始图像,a1到a7是经过几何变换之后的图像,a1～a3分别为图a按照逆时针旋转20°、30°、60°的图像,a4是平移后的图像,a5～a7是放大倍数分别为4、10、20之后得到的图像,a8～a11是纹理库中图像.

图4 来自Brodatz的部分实验纹理图像

在对每幅纹理图像进行特征提取时,获得了m ×r维的特征矢量,如果直接输入神经网络进行训练,势必增加神经元的个数,造成训练速度放慢.由于通过SVD分解所获得的对角矩阵的奇异值是非零递减的,图像的能量主要集中在较大的几个奇异值上,因此对每幅图像的18个对角矩阵,我们只需取前面最大的4个奇异值即可.通过实验证明,这种取法是合理的,最后得到一个72维的特征矢量.

在实验中,我们选取了8类纹理图像,其中每类由15幅图像(其中有通过几何变换得到的图像)组成.从每类中任选10幅共80幅图像组成训练集,其余作为测试集.在建立BP网络时,输入层的神经单元数为72,与特征矢量的维数保持一致,输出层的单元数为8,即为图像类的个数.通过实验证明,隐层单元数为10能获得较好的分类效果.取神经网络的学习速度为0.04,最大迭代次数为1 000次,误差目标值为0.003;取遗传算法的初始种群大小为40,最大遗传代数为80,交叉概率为0.8,变异概率为0.01,初始权值的取值范围为-8～8.我们分别用BP算法和改进的BP算法对网络进行训练,并将所得到的分类结果与文献[12]中的SVM分类方法的结果进行比较,其数据如表1所示.

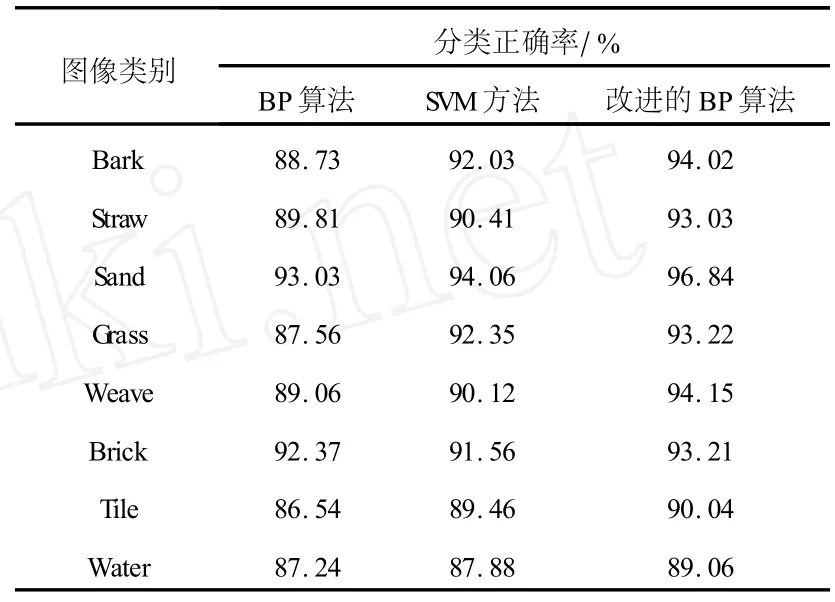
表1 不同算法的分类正确率

从表1中可以看出,SVM方类方法较BP算法的平均分类正确率高出1.69%,但却比改进的BP算法的平均分类正确率低2.04%.针对纹理图像的几何变换,本文算法更具鲁棒性,分类正确率优于文献[12]所述方法.

另外,我们也对8类纹理图像分别用Gabor滤波器、DWT进行纹理特征的提取,并与本文所用DTCWT提取的纹理特征进行了对比实验,其分类正确率如图5所示.

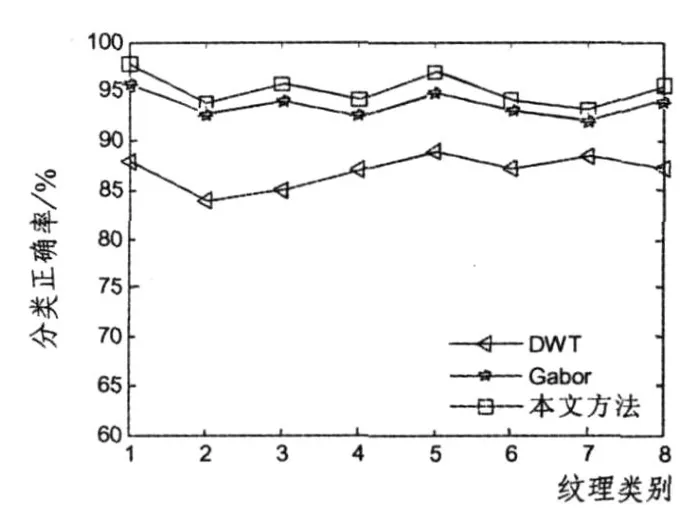
图5 三种纹理特征提取方法的分类正确率

从图5中可以看出,Gabor纹理特征和DT-CWT纹理特征较DWT的分类正确率高,并且使用DTCWT提取出的纹理特征的分类正确率较Gabor纹理特征平均高出2.25%.

5 结 论

为快速对纹理图像进行分类,本文提出了一种基于DT-CWT和SVD的纹理分类算法,该算法充分利用了DT-CWT具有近似平移不变性和较好方向选择性,且能对图像进行完全重构的特点,从图像中提取纹理特征,然后对纹理特征进行奇异值分解获得具有旋转和尺度不变性的特征向量,利用BP网络作为分类器,并用改进的BP算法(遗传BP算法)训练网络,使网络很快得到收敛,而找到全局最优解.初步的实验结果证明了本文所提算法的有效性,且本文算法稍加扩展还可以应用于其他的系统如图像检索中去.

[1]Randen T,Husoy J H.Filtering for Texture Classification:A Comparative Study[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(4):291-310.

[2]Mallat S G.A Wavelet Tour of Signal Processing[M].San Diego: Academic Press,1998.

[3]Wouwer G V,Scheunders D V.Statistical Texture Characterization from Discrete Wavelet Representations[J].IEEE Transactions on Image Process,1999,8(4):592-598.

[4]Dunn D,Higgins W E,Wadeley J.Texture Segmentation Using 2-D Gabor Elementary Functions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1994,16(2):130-149.

[5]K ingsbury N G.Dual-tree Complex Wavelet Transform:A New Efficient Tool for Image Restoration and Enhancement[C]//EUSIPCO98,Proc European Signal Processing Conference.London:IEEE Press,1998:319-332.

[6]练秋生,尚 燕,陈书贞,等.基于DT-CWT和SVM的纹理分类算法[J].光电工程,2007,34(4):109-113.

[7]Liu C C,Dai D Q.Face Recognition Using Dual-Tree Complex Wavelet Features[J].IEEE Transactions on Image Processing, 2009,18(11):2593-2599.

[8]Hong Z Q.Algebraic Feature Extraction of Image Recognition [J].Pattern Recognition,1991,24(3):211-219.

[9]王文胜,陈伏兵,杨静宇.一种基于奇异值分解的特征抽取方法[J].电子与信息学报,2005,27(2):294-297.

[10]G oldberg D.Genetic Algorithms in Search,Optimization and Machine Learn[M].London:Addison-Wesley Publishing Company Inc,1990.

[11]Brodatz P.Textures:A Photographic Album for Artists and Designers[M].New Y ork:Dover,1996:9-112.

[12]Mumtaz A,G ilani S A M,Jameel T.A Novel Texture Image Retrieval System Based on Dual Tree Complex Wavelet Transform and Support Vector Machines[C]//The2th International Conference on Emerging Technologies.Peshawar:Pakistan,2006: 108-114.