利用交换群研究群在集合上的作用的像集

高 茜,杨 凡,葛荣会

(成都理工大学信息管理学院,四川成都 610059)

0 引 言

从同态映射与同构映射是一种包含关系可知,同态映射的原像集与像集有很多性质并不像同构映射那样完全等价[1].而群在集合上的作用本质上仅是一个同态映射,而并不一定是同构映射.交换群是一类特殊群,群在集合上的作用是否能使得其原像集与像集是交换群的这一性质相互等价,是我们在本文中将讨论的问题.进一步考虑群在集合上的作用与其逆作用既有区别又有联系,故群在集合上的作用的像集是否为交换群,与群在集合上的该作用是否是其逆作用之间应存在某种联系,本文对此也进行了讨论.

1 预备知识

定义1[2]设α:G→H是群同态映射,则,

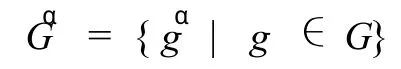
称为同态α的像集.

定义2[3]Hamilton四元数的单位,±1、±i、± j、±k,在乘法下组成一个8阶群,称为四元数群,记为Q8,且 Q8中元素的乘法满足,

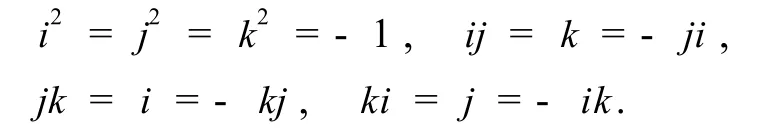
定义3[4]一个群,假如它的结合法还满足交换律,

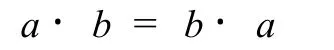
该群就称为交换群或Abel(阿贝尔)群,否则称为非交换群.

定义4[2]设Ω ={α,β,γ…}是一个非空集合,其元素称为点.SΩ表示Ω上的对称群.所谓群 G在Ω上的一个作用φ,是指 G到SΩ内的一个同态.即对每个元素x∈G,对应Ω上的一个变换φ(x):α |→αx,并且满足,

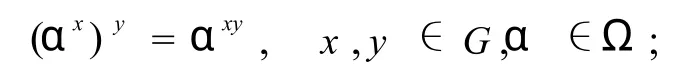
或者,

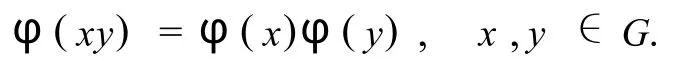
定义5[5]设Ω ={α,β,γ…}是一个非空集合,其元素称为点.SΩ表示Ω上的对称群.所谓群 G在Ω上的一个逆作用φ,是指G到SΩ内的一个逆同态[6].即对每个元素 x∈G,对应Ω上的一个变换φ(x):α|→αx,并且满足,

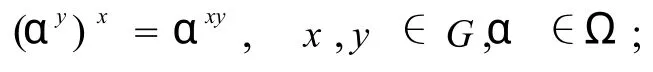
或者,

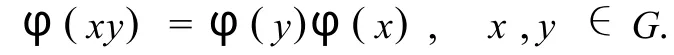
2 主要结论

下述命题均是在φ是群G在集合Ω上的一个作用的前提下进行讨论的.

命题1 如果群 G是交换群,则群 Gφ是交换群.

证明 ∀φ(x),φ(y)∈Gφ,有x,y∈G.由群G是交换群,有 xy=yx,则,φ(xy)=φ(yx).又由φ是群G在集合Ω上的一个作用可知,

通过搜索引擎的site语法对指定目标SNS进行信息检索，构造site：a.com b语句，此时返回a.com中所有包含b的网页。使用爬虫进一步通过正则匹配页数，构造循环，可以获取所有百度返回页面的跳转URL。为了可以获得所有信息的浏览权限，利用requests库构造含cookie包，进一步请求之前返回的URL列表。这是便进入的指定的SNS，通过编写爬虫获取并筛选泄露隐私的用户账号。

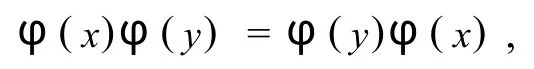
注意到φ(x),φ(y)的任意性,故Gφ是交换群.

命题2 如果群Gφ是交换群,则群G不一定是交换群.

对此命题可举反例进行说明.

群 Gφ是交换群,群 G可能出现以下两种情况:第一种,群 G是非交换群(见例1);第二种,群 G是交换群(见例2).

例1 取群G=Q8,集合Ω={1,2,3}.规定群Q8在 S3上的作用φ满足,

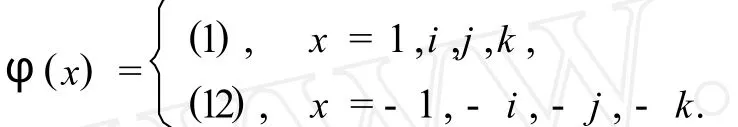
显然,群Gφ={(1),(12)}.这里,群Gφ={(1), (12)}是交换群,但群 Q8却是非交换群.

例2 取群G={±1,±i},集合Ω={1,2,3}.规定群 G={±1,±i}在S3上的作用φ满足,

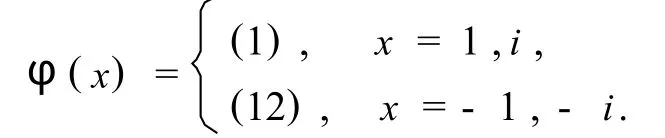
命题3 若Gφ群是交换群,则群在集合上的作用φ即为其逆作用.

证明 φ是群G在集合Ω上的作用,即对每个元素x∈G,对应Ω上的一个变换φ(x):α|→αx,并且满足,

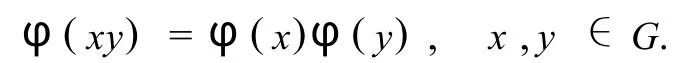
又 Gφ是交换群,有φ(x)φ(y)=φ(y)φ(x), φ(y),φ(x)∈Gφ,则,

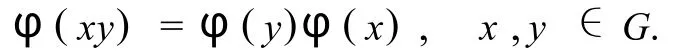
故对每个元素 x∈G,对应Ω上的一个变换φ(x):α|→αx,并且满足,

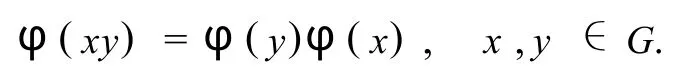
即,φ是群G在集合Ω上的一个逆作用.

命题4 若群Gφ是非交换群,则群在集合上的作用φ必不是其逆作用.

证明 采用反证法.设结论不真,则群在集合上的作用φ是其逆作用,此时有,

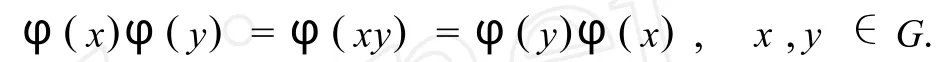
故群 Gφ是交换群,与题设矛盾.

结合命题3和命题4,可得出群 Gφ是交换群与群在集合上的作用φ即为其逆作用之间是充要条件.显然,当群Gφ是非交换群时,群在集合上的作用φ也不是其逆作用,在这种情况下,情况将变得复杂.如何利用已知的群在集合上的作用去找到它的逆作用,以及群 G除了是交换群外,还有哪些情况可以共同构成使得群Gφ是交换群的必要条件,是值得进一步研究的问题.

[1]熊全淹.近世代数[M].武汉:武汉大学出版社,2004.

[2]徐明曜.有限群导引(上)[M].北京:科学出版社,2007.

[3]王世民.Hamilton群[J].西北师范大学学报(自然科学版),1985,21(1):1-4.

[4]魏贵民.现代数学基础[M].北京:高等教育出版社,2007. [5]高 茜.群在集合上的逆作用[J].重庆文理学院学报(自然科学版),2009,28(5):15-17.

[6]任祯琴,张 良,郭继东.群上的逆同态[J].伊犁师范学院学报(自然科学版),2009,3(4):13-15.

[7]李世荣,史江涛,何宣丽.交换群和循环群的若干充分必要条件[J].广西科学,2006,13(1):1-3.

[8]刘 静.关于Abel群同态的扩张[J].山东大学学报(理学版),2010,45(6):39-42.