基于Matlab的直流电阻率三维数值模拟及可视化

彭 淼,熊 杰

(中国地质大学(北京) 地球物理与信息技术学院,北京 100083)

基于Matlab的直流电阻率三维数值模拟及可视化

彭 淼,熊 杰

(中国地质大学(北京) 地球物理与信息技术学院,北京 100083)

针对直流电阻率法的三维正演问题,采用积分方程法的数值解法,特别地,对板状体三维模型做了具体的网格剖分,在Matlab下编程实现了求解其电位分布的算法.根据电位分布分别采用中间梯度法,三极剖面法和联合剖面法计算了地面的视电阻率分布.结果表明,视电阻率异常图充分显示了积分方程求解的正确性.对于该结果,在Matlab中采用G UI编程生成了更为方便的人机交互式正演界面,该界面具有直观、高效的特点.关键词：Matlab;积分方程;直流电阻率法;三维正演;G UI

0 引 言

直流电阻率法是地球物理勘探中一种常用的方法.它是以岩矿石导电性差异为基础,通过观测、研究人工建立的地下稳定电流场的分布规律以达到找矿和解决其他地质问题为目的的一种电法勘探方法[1].研究直流电阻率三维正演问题是电法勘探中的一项重要任务,近30年来国内外已有不少学者对该问题采用有限单元法、有限差分法、积分方程法等数值模拟方法进行了算法研究,成果显著[2-4].

本文采用积分方程法进行直流电阻率的三维正演.对于该正演问题,周熙襄等[1]详细阐述了积分方程的近视求解方法,并对具体模型作了正演计算.他们实现该算法是用FORTRAN语言编写的,而本文采用可视化功能更为强大的Matlab来实现.笔者不仅最终成功实现了直流电阻率的积分方程法三维正演算法的高效计算,而且还采用G UI编程开发了正演用户界面,这使得方便、快捷的人机交互式正演成为可能.

1 积分方程及其求解方法

假设在无限大半空间的均匀介质中,存在一个三维地质体,它的电性与周围介质的电性不同.位于地面的一个电流源供给稳定电流 I,均匀介质的电阻率为ρ1,三维地质体的电阻率为ρ2,表面电荷密度为 q.根据基本的电场和电磁场定律及边界条件,可以导出如下积分方程：

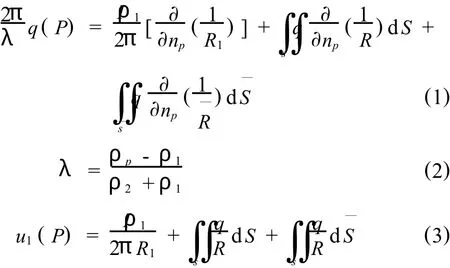
式(1)、(2)为电阻率突变界面积累电荷密度 q所满足的积分方程式.当外电源和电阻率分布给定时,求解式(1)、(2)即可得到 q的分布.通过已知的q分布求解式(3)便可以计算出空间任意点的电位.

对于上面的积分方程,要给出其解析解是很困难的,本文采用数值计算的近似解法,其具体步骤如下：

首先,将积分域离散化为有限个小面积的组合.然后,将每一个小面积用一个简单的平面近似代替.设小平面内的q为常数,这样,积分方程就变成了一组线性方程组：

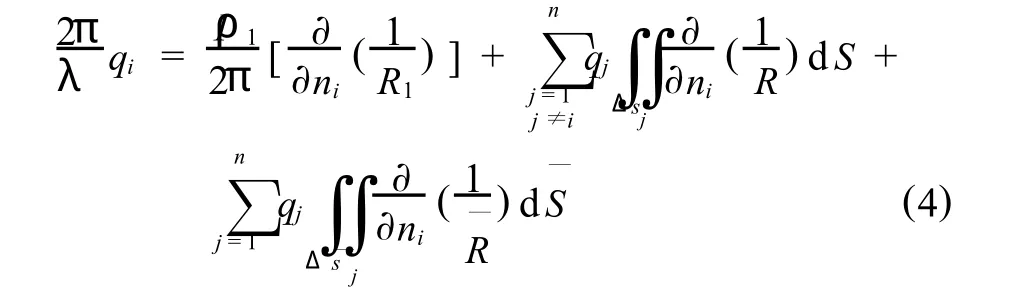
式中,qi(或qj)为第i个(或第j个)小平面内的积累电荷密度,它在该小平面内为一常数,Δsj(或Δs—j)为小面元的面积.

式(4)中,当i=1,2,…,n时,可以得到n个线性方程,组成一个 n阶线性方程组,其矩阵方程为,

其中,系数矩阵A的对角线元素为,

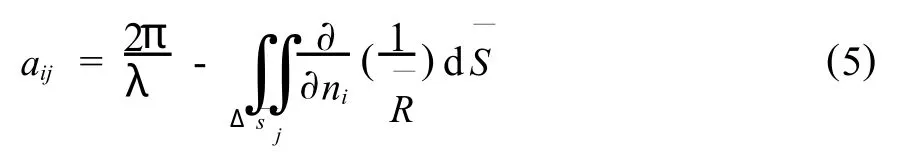
非对角线元素为,

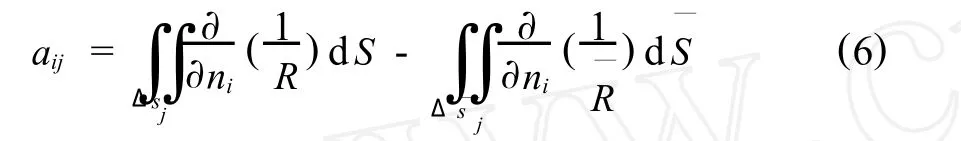
右端项为,

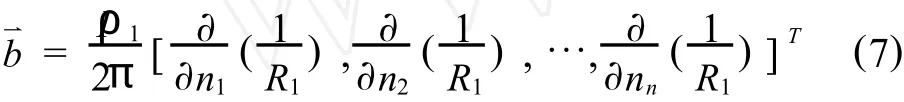
然后,对系数矩阵各元素中的面积分项进行计算,有以下近似表达式：

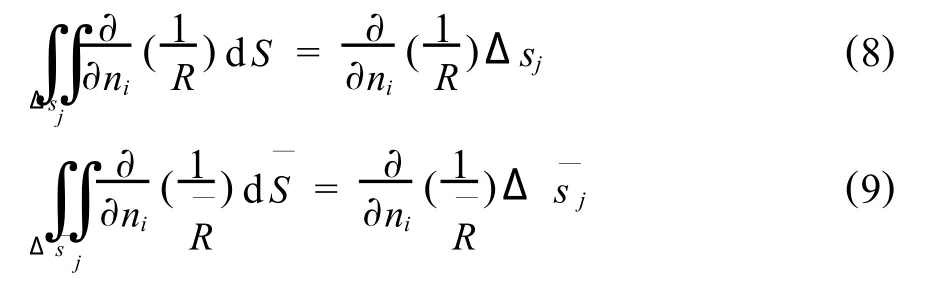
将式(3)～(9)联立起来求解,就可以得到q的分布,此即为积分方程(1)的数值近似解.

2 板状体三维模型

上述积分方程的数值近似求解方法适用于任意形体的三维模型计算.本文采用的是板状体三维模型(见图1).图1中上部的长方体代表虚源.

图1 板状体三维模型示意图及表面网格剖分

对于一个长、宽、高分别为A、B、C的板状体,本文采取以下方式划分表面的小面元：把长方体的每条棱划分成N段,其中 a=A/N,b=B/N,c= C/N,那么共出现3种不同的小面元,a×b,b×c和c×a,一共有6×N2个小面元.这样划分的优点是避免了奇异面元的讨论,从而能很方便地实现算法.

由于每一个划分得足够小的面元内的积累电荷密度 qi都可以视为常数,故对于式(4)、(5)、(6)中的积分项,可以采用下列近似公式求解：

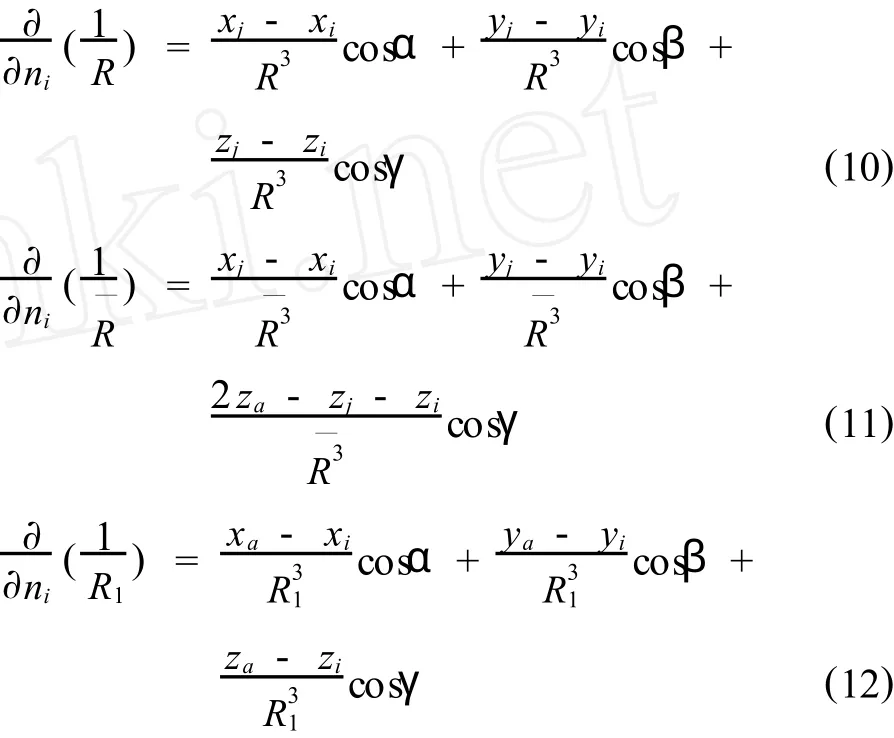
通过对板状体上顶面、底面、前侧面、后侧面、左侧面以及右侧面的分类讨论,计算系数矩阵和右端项,并求解线性方程组可得到q的分布,然后利用下式计算地表任意点的电位：

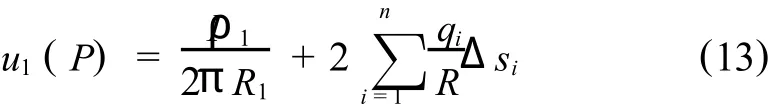
最后,本文在Matlab的编程环境中实现了计算地表电位分布的算法,并将程序模块保存于相应文件中.

3 视电阻率的计算及算例

为了检验程序的有效性和正确性,本文分别采用中间梯度法、三极剖面法以及联合剖面法计算得到了地表的视电阻率分布.计算时均采用以下公式：

对于三极剖面法和联合剖面法,其装置系数为,

而对于中间梯度法,除计算主测线上的视电阻率值外,还可计算在离开主测线上一定距离且与之平行的旁测线上的视电阻率值,其装置系数为：

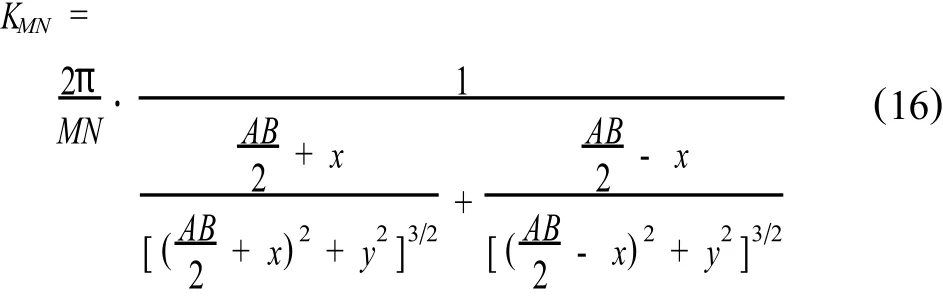
中间梯度法板状体三维模型正演主测线视电阻率对比如图2所示.

实线参数如下：顶部埋深为5 m的板状体：长B=20 m,宽A =10 m,高C=10 m;直流电源位于地面主测线,相距AB= 420 m;电流I=20 A;围岩电阻率ρ1=1 000Ωm;板状体电阻率ρ2=20Ωm;测量电极MN=2 m.其他曲线参数除长和围岩电阻率按图例改变外,其余不变.图2 中间梯度法板状体三维模型正演主测线视电阻率对比

从图2的对比可以看出,其视电阻率曲线完全符合理论解释,即：都在模型中点出现低阻异常极小值;都在远离模型的两侧接近围岩真实电阻率;靠近模型两侧都出现小的极大值.这说明正演结果是稳定可靠的.

由于三维正演可以得到地面任意位置的电位,根据该点电位可以计算地表视电阻率的分布.图3、图4和图5是分别采用中间梯度法,三极剖面法以及联合剖面法计算得到的地面视电阻率的分布图.这3张图都很直观地显示了板状体的大致位置.其中：图3中心的低阻异常与板状体中心位置吻合;图4和图5的对比也进一步说明了正演结果的正确性.

参数设置：顶部埋深为5 m的板状体,长B=20 m,宽A= 10 m,高C=10 m;电流I=20 A;围岩电阻率ρ1=1 000 Ωm;板状体电阻率ρ2=20Ωm;测量电极MN=2 m.图3 中间梯度法板状体三维模型正演地表视电阻率平面图

参数设置：顶部埋深为10 m的板状体,长B=10 m,宽A= 10 m,高C=6 m;AM=8 m;MN=2 m;电流I=20 A;围岩电阻率ρ1=500Ωm;板状体电阻率ρ2=50Ωm.图4 三极剖面法板状体三维模型正演地表视电阻率平面图

参数设置：顶部埋深为10 m的板状体,长B=10 m,宽A= 10 m,高C=6 m;AM=8 m;MN=2 m;电流I=20 A;围岩电阻率ρ1=500Ωm;板状体电阻率ρ2=50Ωm.图5 联合剖面法板状体三维模型正演地表视电阻率平面图

需要说明的是,以上图示结果的正演计算均采用6×10×10的网格剖分,与更为精细的6×15×15的网格剖分仅存在0.38%的平均误差,而以上图示的数值计算和成图的时间只需4～8 s(计算机的配置为：英特尔酷睿2双核E4500CPU,2 G内存).因此,该程序在Matlab平台上的运行是高效的.

4 GUI界面设计

对于上述正演模拟,我们通过修改模型参数可以获得若干种正演结果.但是,每次修改参数都需要在程序代码中进行,这样既费时又费事,给正演研究过程带来诸多不便.为解决这一问题,我们在Matlab平台上采用G UI编程设计了人机交互式正演界面.

人机交互式正演界面的右侧是参数输入面板和操作控制台,其中集成了中间梯度法、三极剖面法以及联合剖面法3种方法求解地表视电阻率.用户只需依次输入想要改变的参数值,然后左键单击正演模拟按钮便能完成从数值模拟到成图的所有过程.人机交互界面的左侧是成图区,包含了模型的三维立体图以及正演结果图.其中模型的三维立体图可以分二维和三维变换显示.采用G UI编程用户从正演开始到成图结束的等待时间只需4～8 s,且正演过程能够重复进行.图6显示了采用中间梯度法正演模拟完成后的用户界面.

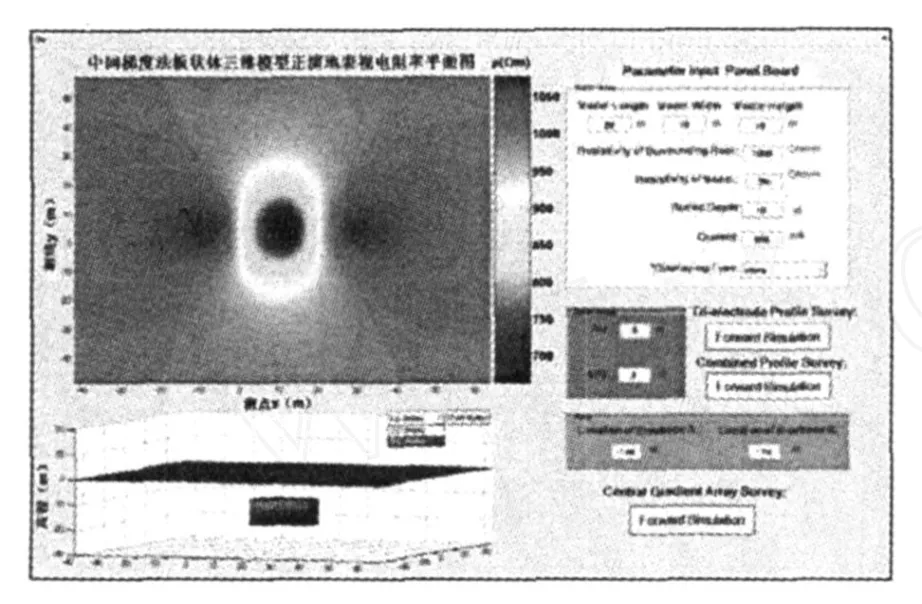
图6 中间梯度法板状体三维模型人机交互式正演界面图

5 结 语

本文利用经典的解三维问题的积分方程法进行数值模拟,目的不在于对该算法进行突破创新,而在于提出一种能在Matlab平台上解决电法正演问题的思路.同时,我们开发的人机交互式正演界面只是一个初步尝试,却已具备简洁、直观、快速等诸多优点,相信通过引入更多的正演程序模块以及G UI编程的进一步拓展,其能够发展成为功能更为强大的正演模拟系统.

[1]周熙襄,钟本善.电法勘探数值模拟技术[M].成都：四川科学技术出版社,1986.

[2]李金铭.地电场与电法勘探[M].北京：地质出版社,2004. [3]傅良魁.应用地球物理教程[M].北京：地质出版社,1991. [4]江玉乐,雷 宛.地球物理数据处理教程[M].北京：地质出版社,2006.

[5]顾观文.电阻率/激电测深二维人机交互正演模拟[J].物探化探计算技术,2007,29(S1)：89-105.

[6]李晓昌.在Matlab平台上实现可控源音频大地电磁反演数据三维可视化显示[J].物探化探计算技术,2007,29 (S1)：68-104

3-D Numerical Simulation and Visualization of DC Resistivity Based on Matlab

PENG Miao,XIONG Jie

(School of Geophysics and Information Technology,China University of Geosciences,Beijing 100083,China)

Integral equation method was used in this paper to solve the 3-Dforward problemof DC resistivity.Especially,specific gridding dissection was made on the 3-D tabular model and an algorithm for solving its potential distribution was realized by programming on Matlab.Central gradient array,tri-electrode profile and combined profile survey were utilized to calculate its apparent resistivity distribution on ground according to the potential distribution.The results indicate that this solution of the integral equation is correct according to apparent resistivity anomalyfigure.Besides,a human interface for more convenient forward stimulation was created by G UI programming on Matlab.This interface is intuitive and efficient.

Matlab;integral equation;DC resistivity;three-dimensional forward simulation;G UI

P631.3+25

：A

2010-07-25.

彭 淼(1963—),男,博士研究生,从事电法勘探技术研究.

1004-5422(2010)03-0213-04