自适应变异粒子群优化算法
2010-01-06黄继红苏守宝陈振伟
黄继红,苏守宝,马 艳,陈振伟
(皖西学院计算机科学技术系,安徽六安 237012)
自适应变异粒子群优化算法
黄继红,苏守宝,马 艳,陈振伟
(皖西学院计算机科学技术系,安徽六安 237012)
提出了一种自适应变异粒子群优化算法,该算法通过遗传变异提高种群多样性的方法使算法增强持续搜索能力,解决了PSO算法的早熟收敛问题。采用标准测试函数进行仿真实验,结果表明:提出的算法具有提高局部最优值的能力,且优化精度更高。
粒子群优化;遗传算法;变异;自适应性
粒子群优化算法:粒子群优化(Particle Swarm Optimization,PSO)算法是一种进化计算技术,由Eberhart博士和 Kennedy博士发明。算法源于对鸟群捕食的行为研究。
PSO算法着重强调种群的社会属性,通过模拟群体的社会行为实现对空间的搜索,与GA算法相比较,粒子群算法需要调节的参数不多,不需要对变量进行二进制编码,而且在迭代过程中不需要进行交叉、变异等遗传操作,而以粒子的速度参数进行路径搜索。由于粒子群算法中目标函数即为适应度函数,故省去了GA中从目标函数到适应度函数的转换。因此,粒子群算法在多数情况下能较遗传算法更快地收敛于全局最优解[1]。
PSO算法虽然具有收敛速度快、易实现、易理解并且仅有少量参数需要调整的优点,但也有自身的不足之处。对高维复杂问题,粒子群算法常出现早熟收敛,陷入局部极小。
针对基本PSO算法的不足,本文对粒子群算法的收敛性进行了研究,并根据遗传变异能增加种群多样性的特性给出了改进型算法,即自适应变异粒子群优化(Particle Swarm Optimization with Adaptive Mutation,AMPSO)算法。
1 AMPSO算法
1.1 基本粒子群算法
PSO算法是对鸟群捕食行为的研究,经过抽象,鸟被抽象为没有质量和体积的粒子(点),并延伸到n维空间,每个粒子分别由位置向量 Pi=(P1,P2,… Pn)和速度向量Vi=(V 1,V 2,…,Vn)表示,都有一个由目标函数确定的适应值(fitness value),并且知道自己到目前为止发现的最好位置(pbest)和现在的位置Pi.,这个可以看做粒子自己的飞行经验。另外,每个粒子还知道当前整个群体中所有粒子发现的最好位置(gbest),其中 gbest是pbest中的最好位置。把这个值可以看作粒子群体经验。每个粒子通过自己的经验和群体经验来决定下一步的运动行为[2]。
PSO算法首先对这群粒子初始化,并通过迭代找到最优解。在每一次迭代中粒子通过跟踪两个“极值”来更新自己。公式(1)、(2)为 PSO算法的标准公式。

其中,T为迭代次数vi、Pi、pbest、gbest如前定义;Rand()是介于(0,1)之间的随机数;C1、C2为学习因子,一般C1=C2=2.;ω为惯性因子;在每一维,粒子都有一个最大限速度Vmax(Vmax>0),如果某一维的速度超过设定的Vmax,则该维速度被限定为Vmax[3]。
1.2 AMPSO算法
针对基本粒子群优化算法的不足,一些学者对粒子群算法,以不同途径,作了各式各样的改进。本文是通过遗传变异算子来提高种群多样性的途径实现标准粒子群算法的改进。
遗传中的变异算子,一方面可以提高算法的局部搜索效果;另一方面可以使群体进化过程中丢失的等位基因信息得以恢复,以保持群体的个体差异性,防止发生早熟收敛。可以借鉴这一思想,来改善粒子群优化算法在搜索过程中可能出现的多样性丢失的情况。即对整个粒子群位置向量引入变异概率因子,以扩大对解空间的搜索范围,使算法能有效地进行全局搜索,从而增加了粒子收敛到全局最优解的概率。
但是过大的变异率在增加种群多样性的同时也将会导致群体发生混乱,使种群不能进行精确局部搜索,减缓算法的收敛速度。而过小的变异率,不能快速、有效地逃出局部极小点。所以“变异”的特性必须根据当前环境的变化而调整变异率因子的大小,从而增强变异的自适应性[2]。本文把这种改进的粒子群算法称为自适应变异粒子群优化算法(Particle Swarm Optimization with Adaptive Mutation,AMPSO)。
算法如下:
在粒子群算法迭代过程中,判断粒子群最优粒子位置是否在不断变化或变化很小,可通过设置一个粒子群最优位置连续不变化次数的阈值,当粒子群最优粒子位置连续不变化或变化极小的迭代次数大于阈值时,认为有集聚倾向,即出现早熟收敛。
如果有集聚倾向,对整个粒子群位置向量按随机变异概率因子发生变异。每一次迭代过程中,粒子更新完速度向量和位置向量后,判断是否集聚。若是,位置根据变异因子发生变异;若否,则正常循环迭代。
粒子结点位置向量变异公式如公式(3):

其中,pm为变异算子,Rand()取(0,1)之间的随机数,C为变异因子[4]。
2 AMPSO算法实现
自适应变异粒子群优化算化流程见图1。

图1 自适应变异粒子群优化算法流程
PSO算法中自适应变异代码实现过程:

其中,m为当前已迭代次数,Mmax为粒子群进化到Mmax代后发生变异,Nmax最优粒子适应度值稳定不变的代数阀值,popSize为粒子群规模,Pmax为位置向量每一维的最大值,P为粒子位置向量矩阵,N为每个粒子向量维数。
3 仿真实验与结果分析
为验证本文提出的自适应变异粒子群算法(AMPSO)性能,在MATLAB环境下做了实验仿真,并与基础粒子群算法及遗传算法(GA)进行比较。
在实验中,三种算法所用参数相同或相似,具体参数为:种群个数为50,迭代次数为500,运行100次,AMPSO算法的变异概率为0.8,最优值连续不变阈值为10。遗传算法采用实数编码。
并采用一下标准测试函数:


对于Rastrigin函数,当误差小于0.003时,找到最优解;Rosnebork函数在xi=l,(i=l,2,…n)处达到的全局极小值0;对于Schaffer’s f6函数,突破局部极大值点.09903,就算找到最优解:而Schaffer’s f7函数在 =0,(i=,1,2,…n)处达到全局极小值0。试验的结果如表l所示:

表1 三种算法仿真结果比较
由表1实验结果分析可知,AMPSO算法无论是在正确收敛的次数,还是在搜索到的最优值的平均值方面都要优于 PSO算法和 GA算法,例如对于Schaffer’s f6函数能够达到100%的正确收敛,而且精度也很高。AMPSO算法在收敛速度方面也有其优势。
三种算法对四个函数的优化曲线的比较如图2—图5所示:
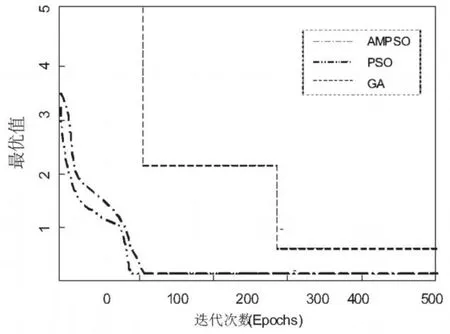
图2 函数Rastrigin优化比较

图3 函数Rosnebork优化比较

图4 函数Schaffer’s f6优化比较

图5 函数Schaffer’s f7优化比较
对图2—图5的分析可以发现:遗传算法收敛最慢,且能够达到的精度也是最低的;而基本PSO算法收敛的速度都是最快的,但是一旦陷入局部最优值后,PSO算法就无法再有突破,这正符合基本 PSO算法收敛速度快,但是易早熟的特点,AMPSO算法的收敛速度大体与基本PSO算法相当,但是有很强的突破局部最优值的能力,最终能够达到的优化精度也是最高的。这充分说明了AMPSO算法在函数优化方面的优势。
4 结论
自适应变异粒子群算法实际上是在标准粒子群优化算法的基础上,根据环境的变化,增加变异操作来提高算法跳出局部收敛的能力。仿真实验结果表明:该算法的收敛速度快,迭代次数较少,精确率高,其算法思想更接近于自然进化规律。
[1]A Banks,J Wincent,C Anyakoha.A Review of Particle Swarm Optimization.Part I:Background and Development [J].Nat Comput:An Int J,2008,6(4):467-484.
[2]肖晓丽,黄继红,刘志鹏.基于变异PSO的BP网络及入侵检测中的应用[J].计算机工程,2008,30(24):1030 -1033.
[3]苏守宝,汪继文,方杰.粒子群优化技术的研究与应用进展[J].计算机技术与发展,2007,17(5):249-253.
[4]P Asokan,J Jerald,S Arunachalam,et al.Application of A-daptive Genetic Algorithm and Particle Swarm Optimisation in scheduling of jobs and AS/RS in FMS[J].International Journal of Manufacturing Research,2008,3(4):393 -405.
Particle Swarm Optimization Algorithm with Adaptive Mutation
Huang Ji-hong,Su Shou-bao,Ma Yan,Chen Zhen-wei
(Department of Computer Science and Technology,West Anhui University,L u’an237012,China)
A particle swarm optimization algorithm with adaptive mutation(AMPSO)is presented in this paper.The algorithm of genetic variation through increased population diversity means to make the algorithm of continuing the search capabilities of the PSO algorithm to overcome the phenomenon of premature convergence.Adopting well-know n benchmark test functions Rosenbork function simulation experiments,it show s that the proposed algorithm has a strong breakthrough in the capacity of local optimal value and optimal precision.
particle swam optimization;genetic algorithm;mutation;adaptive
TP183
A
1009-9735(2010)02-0027-04
2009-10-20
安徽省自然科学基金项目(090412261X);安徽高校省级自然科学重点项目(KJ2007A 072,KJ2007A 087)。
黄继红(1977-),男,安徽六安人,硕士,研究方向:计算机网络与信息安全;苏守宝(1965-),男,博士,教授,研究方向:群智能与控制优化。
