从复合函数到不动点迭代的探讨

董 毅,李声锋

（蚌埠学院数学与物理系,安徽蚌埠 233030）

从复合函数到不动点迭代的探讨

董 毅,李声锋

（蚌埠学院数学与物理系,安徽蚌埠 233030）

复合函数是高等数学的重要内容之一,而不动点迭代是理工科学生要求掌握的一个基本概念。在高等数学中,通过对复合函数有关知识的教学,适时地引出不动点迭代的概念,并自然地对相关理论进行了一些探讨。

复合函数;不动点;迭代

1 引言

在高等数学中,复合函数是教学的重要内容之一[1]（P14-16）[2]（P22-25）。对其知识的掌握,不仅能加强对初等函数概念的理解,而且能更好地帮助对导数和积分的学习。在理论或工程技术实践中,不动点迭代常常是一个重要概念,要求理工科学生能够掌握并能灵活应用。笔者在高等数学课程的教学中讲解复合函数的有关知识时,适时地引出不动点迭代的有关知识。这样做不仅开拓了学生视野,同时夯实了对复合函数有关知识的理解,而且获得了较好的教学效果。

2 复合函数概念

复合函数是说明函数对应法则的某种表达方式的一个概念。利用对应关系传递的原则,将两个或多个函数通过中间变量的“桥梁”作用,产生新的函数,这一过程就是函数的复合。利用这一概念,一方面可以由几个函数产生新的函数,另一方面也可以把函数“分解”成几个简单函数。比如:

例1函数z=u和u=x（x-2）复合产生新的函数z=x（x-2）。在此复合过程中,要注意确定复合函数定义域。这里的复合函数要求x（x-2）≥0,即得到复合函数的定义域为x∈（-∞,0]∪[2,+∞）。

例2函数z=arccosu和u=x2+3就不能复合成一个复合函数。因为对于u=x2+3的定义域R中任意x对应的u值,都不能使得函数z=arccosu有意义。

例3函数z=sin3（x+1）可以“分解”为z=u3、u=sinv和v=x+1三个简单函数。

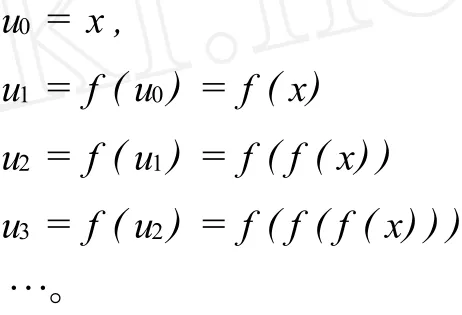
3 从复合函数到不动点迭代

有了复合函数的概念之后,我们可以考虑同一个函数的复合过程。比如,给出简单函数u=f（x）,对任意k∈N,令

上面过程产生序列{uk},k=0,1,2,…。容易看出,序列{uk}满足

复合关系,这一关系又称为递推关系或者迭代关系。这样我们就自然地得到了迭代的概念,即

定义1由一个初始值u0=x出发,按照公式（1）进行计算得到序列{uk},这一过程称之为迭代。

例4设函数f（x）=2x,则k次迭代得到uk=2k x。

公式（1）的迭代思想,在工程技术上或者理论上都有很重要的应用。比如在计算机的程序设计中,递归调用（也即迭代）是常见程序设计之一。在利用数学工具研究社会现象和自然现象,或解决工程技术等问题时,很多问题可以归结为非线性方程的求根,而迭代思想是求解方程的一种重要方法[3]（P18-23）[4]（P50-55）。设非线性方程F（x）=0,将其换成等价形式（简单的一种方法是x=x-F（x））

定义2设x＊是方程F（x）=0的一个根,则x＊也满足等式（2）,即x＊=f（x＊）,反之亦然。则称x＊是函数f（x）的一个不动点。

于是,求方程F（x）=0的根就等价地化为求函数f（x）的不动点。

定义3设x＊是方程F（x）=0的一个根。选择靠近x＊的初始近似值x0,按照迭代格式xk+1=f （xk）进行计算得到序列{xk},k=0,1,2,…,这一过程称之为不动点迭代。

现在的问题是不动点迭代产生的迭代序列{xk}是否收敛。如果序列不收敛,则不能得到方程F（x）=0的根,但是对这一问题的进一步研究,可以导致混沌学的产生,这里不再赘述;如果序列收敛,设收敛到x＊,显然x＊就是f（x）的不动点,即方程F（x）=0的根。下面给出在[a,b]区间上函数f（x）的不动点存在且唯一的一个充分条件。

定理1设f（x）在[a,b]上连续,且对任意x∈[a,b]有a≤f（x）≤b成立,则f（x）在[a,b]上一定存在不动点。进一步,如果f′（x）在（a,b）上连续,且存在常数0＜L＜1,使得对任意x∈（a,b）,有

则f（x）在[a,b]上具有唯一的不动点。

证明若f（a）=a或f（b）=b,显然f（x）在[a, b]存在不动点。因为a≤f（x）≤b,不妨设f（a）＞a与f（b）＜b。作辅助函数

显然h（x）在[a,b]上连续,且满足

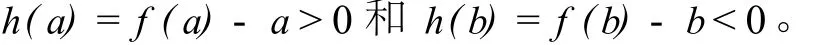
由连续函数性质,一定存在x＊∈（a,b）使得h （x＊）=0,即f（x＊）=x＊,x＊就是f（x）的不动点。

进一步,设f′（x）在（a,b）上连续,且存在常数0＜L＜1使得|f′（x）|≤L,下证不动点是唯一的。假设f（x）在[a,b]有两个不同的不动点和则由微分中值定理,有

其中ξ∈（a,b）。从而引出矛盾。故f（x）在[a,b]上不动点是唯一的。

至此,可以给出压缩映射的概念以及不加证明地给出著名的Banach不动点定理[5]（P275-288）。

定义4设f:D⊂X→Y是一个映射。若存在常数L∈（0,1）,对任意x,y∈D,使得

其中‖x-y‖表示点x∈D与点y∈D之间的距离,则称f为压缩映射。

4 举例

例5利用不动点迭代求方程F1（x）=x2-2= 0的一个正根。

5 总结

在高等数学教学过程中,引入复合函数有关知识之后,可以自然地获得不动点迭代的概念,并对相关理论进行一些探讨。这样做不仅可以增强学生对理论的理解、而且能够开拓学生视野。但从复合函数到不动点迭代的教学和探讨中,诸如哪些类型的函数进行复合会产生周期现象?不动点迭代的初始点如何选择?迭代收敛的速度是多少?这些问题会继续引起我们的思考和研究。

[1]同济大学应用数学系.高等数学（第五版）[M].北京:高等教育出版社,2005.

[2]刘玉琏,傅沛仁,林玎,等.数学分析讲义（上）（第四版） [M].北京:高等教育出版社,2007.

[3]林成森.数值计算方法[M.北京:科学出版社,2001.

[4]R.L.Burden,J.D.Faires.Numerical Analysis（7th Ed.） [M].Calif.:Brooks/Cole Publishing Company,2001.

[5]童裕孙.泛函分析教程[M].上海:复旦大学出版社,2003.

Discussions about Function of Functions to Fixed-point Iteration

DONG Yi,LI Sheng-feng

（Department of Mathematics&Physics,Bengbu College,Bengbu233030,China）

Function of functions is one of important contents of advanced mathematics,while fixed-point iteration,a basic concept, must be mastered by science and engineering college students.The concept of fixed-point iteration is presented in good time and corresponding theories are discussed after teaching some know ledge about function of functions in the advanced mathematics courses.

function of functions;fixed-point;iteration

O13

A

1009-9735（2010）02-0004-03

2010-03-12

安徽省教育厅自然研究重点项目（KJ2010A 237）;安徽省高校优秀青年人才基金项目（2010SQRL118）。

董毅（1957-）,男,安徽芜湖人,蚌埠学院教授,研究方向:经典调换分析;李声锋（1976-）,男,安徽怀宁人,讲师,在读博士生,研究方向:应用逼近论。