空间二次曲线射影重建计算方法研究

张政武

（陕西理工学院机械工程学院，陕西 汉中 723003）

计算机视觉的基本目的之一就是通过分析景物的一幅或多幅图像来揭示景物的本质特征。由于在投影过程中，三维景物的空间关系、物理性质以及表面的物理特性在二维图像中综合为图像点的灰度值，因此，在得到二维图像的过程中丢失了景物的深度信息，正是由于要恢复这种丢失的深度信息便组成了计算机视觉研究的核心问题——从景物图像或序列图像恢复三维景物的形状、位置、运动等物理特征。

将二次曲线作为一个重要的基本要素来实现对三维场景的理解和识别是计算机视觉研究的一个重要的领域。近几年来，研究人员在这方面做了大量的工作，在围绕着二次曲线计算方法的研究方面取得了不少的成绩[1-6]。文献[1]通过对多幅图像中二次曲线上多个点的检测来求解二次曲线；文献[2]中通过对二次曲线上不同直线的检测来实现对二次曲线的恢复；文献[3]利用几何代数来表示二次曲线，通过求解两个不同点上线束的对应直线交点推导出二次曲线的几何积的表达形式；文献[4]、[5]是将一条二次曲线表示为P5射影空间中的一个点或者一个称为二次曲线矢量的六维矢量，然后通过一个6×6的射影变换矩阵推导出了从一个给定的二次曲线基变换为点基的线性算法和两幅图像对应的约束条件，实现了对物体的识别；文献[6]提出一种二次曲线的整体表示法，即给出了空间二次曲线和平面二次曲线的坐标表示法，该坐标是由不全为零的9个数构成的有序数组，建立了基于动态灰度图像和基于序列灰度图像的二次曲线光流的概念。上述方法,总的来说是利用点、直线坐标或是利用矢量运算来对二次曲线进行检测和识别，在实际情况中，由于图像数据存在噪声，通常需要利用迭代法以求解多元方程组的最优解，这就存在迭代法不收敛或收敛到一个局部而非全局的最优解的可能性。本文从实际计算的角度出发，将一条二次曲线表示成一个空间锥面和一个平面的交线，利用两个二次曲面的基曲线推导出二次曲线重建的对应条件，在此基础上，给出了空间二次曲线射影重建的计算方法，最后通过实验验证表明该算法实用、可靠。

1 空间二次曲线的射影重建

1.1 空间二次曲线

射影空间中点和平面互为对偶，因此平面二次曲线的空间对偶就是锥面，同时二次曲线是一 个秩为3的二次包络[7]。设锥面为T0=x Qx （Q是 4× 4的对称矩阵），空间平面为π = pTx =0， 当用平面坐标代替点坐标时，二次曲线的平面方程能够表示成一个空间锥面和一个平面的交线

其中 平面 u=( u1, u2, u3,u4)T是变平面。

1.2 空间二次曲线的射影重建

设双目立体视觉中两个摄像机的投影矩阵分别为P 和P′，射影重建是指确定这对射影矩阵P 和P′之间的射影变换，因此就要在射影空间中研究二次曲线重建的内部特征。

假设给定两幅图像中的一对对应二次曲线

对空间二次曲线进行射影重建就是要寻找空间中的一条二次曲线，该二次曲线分别被投影为C 和C′。由上述分析知道，空间一条二次曲线能够表示成一个空间锥面和一个平面的交线，因此对于空间二次曲面的射影重建问题就是要根据该二次曲线的图像来确定空间锥面和该平面的方程。

定理1设摄像机的投影矩阵分别为P 、P′，则连接摄像机中心O、O′和图像中对应的 二次曲线C 和C′的锥面方程Q 和Q′分别是

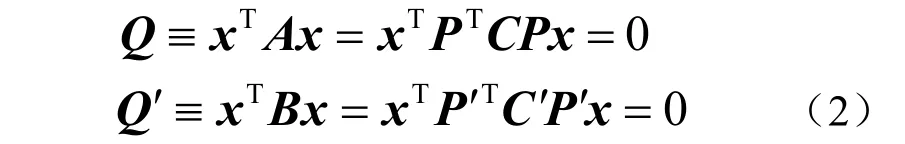
证 明将对应于两个摄像机的投影方程分别代入二次曲线的二次型方程便可得到式(2)。式(2)表示如果空间点x 的投影位于图像二次曲线C （或C′）上，则x 满足式(2)，而且任何位于由O 和C 组成的锥面（或O′和C′组成的锥面）上的点的投影都位于C （或C′）上，因此 式(2)分别为Q 和Q′的锥面方程。

考虑二次曲面束 Q + λQ ′=0，对于每一个λ 的值，方程 Q + λQ ′=0表示一个二次曲面，该曲面通过Q 和Q′所有的公共点。该曲面束中的所有二次曲面的公共点组成一条曲线，该曲线是Q 和Q′交线，并且这条曲线就是该曲面束的 基曲线。两个二次曲面的基曲线一般是一条四次曲线。在本文中，重建约束就是限定这对对应的锥面在空间的交线是一条二次曲线。

由于空间的这条二次曲线是基曲线的一部分，因此束的基曲线就被分为两部分，其中的一部分就是空间的这条二次曲线，同时另外一部分也是一条二次曲线。由于一对平面可以被看作秩为2 的退化的二次曲面，这对退化的二次曲面就组成了一对属于二次曲面束中的一对平面。所以，从两个图像中重建空间二次曲线就等同于寻 找一个λ，使得λ 矩阵 C (λ ) = A+λB的秩为2，此时， xTAx =0和 xTBx =0就是对应于空间二 次曲线的锥面。

1.3 射影重建的对应条件

命题1 对于一对对应二次曲线存在两个独立的多项式条件。

证 明一个4×4 的对称矩阵有10－1＝9个自由度，这样一个矩阵束就有9－1＝8 个自由度；同时，一个秩为2 的4 阶对称矩阵有6 个自由度，于是对于一对对应二次曲线就有8－6＝2个独立条件。

现在推导这两个多项式条件。

考虑λ 矩阵 C (λ ) = A+λB的特征多项式

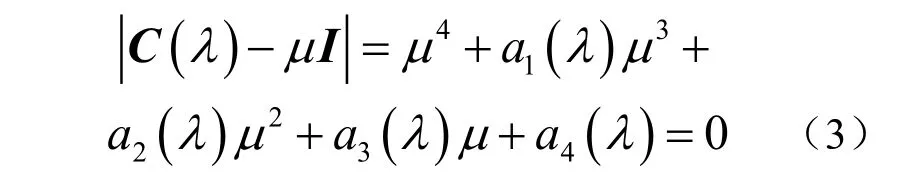
由于 ( )λC 是一个4×4 的是对称矩阵，要使 得它的秩为2，必须有两个不同的非零特征值和两个零特征值，因此对应条件应满足

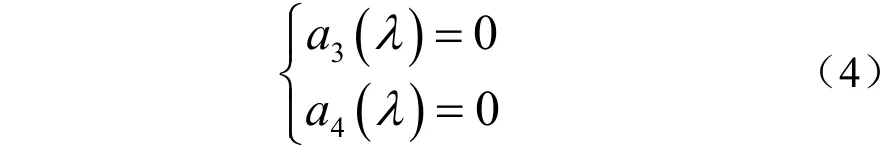
根据定义， a4( λ )是 C (λ )的行列式，这样a4( λ )就是矩阵束 A + λB的特征多项式，并且

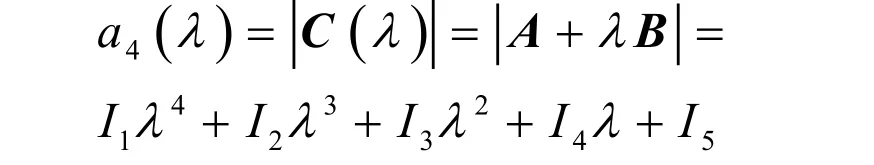
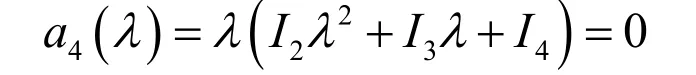
一般情况下， a4( λ )= 0有四个根，每一个 根是束中的一个特征值，并且对应于束中一个矩阵，其中两个特征值分别是 0=λ 和 ∞=λ ，它们分别对应于矩阵A 和B，其余两个特征值是下面二次方程的两个根。

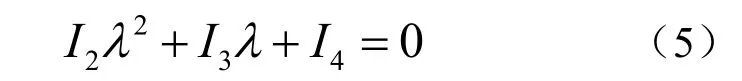
为了在束中有一个秩为2 的矩阵，则必须至少有一个二重特征值，因此式（5）必须有两个相等的根，即

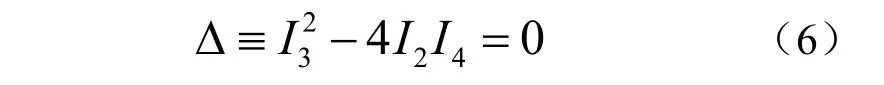
这就是第一个对应条件。

当 a4(λ )= 0的条件被确定之后，下面推导a3( λ )= 0的对应条件， a3( λ )是λ 的一个三次多项式，它可以写为

其中ij 是由矩阵A、B 个元素组成的多项式。

第二个对应条件通过将 a3( λ )、a4(λ )两个 方程联立起来求解λ，再利用 0=Δ 则很容易得到下面的第二个对应条件

因此，一对对应二次曲线的两个多项式的对应条件分别是式（6）和式（7）。

1.4 射影重建的计算方法

1.4.1 退化的二次曲面

因为方程（5）有两个相等的根，所以两个相等的特征值可直接求得，其中

而退化的二次曲面的矩阵 BAC λ+= 。

1.4.2 求解平面对

利用式（7）将矩阵 ( )λC 的特征多项式（3），可以化简为

其中两个非零特征值1μ 和2μ 是下面二次方程的根

因为C 是一个实对称矩阵，因此存在一个变换矩阵T ，可以将矩阵C 转化成一个对角矩阵

相应地将 x = Tx′代入 x′Tdiag ( μ1, μ2,0,0) x′ =0 中，二次曲面 xTCx =0变换为

显然，为了得到实平面，必须使

设 21,vv 分别是矩阵C 的特征值 21,μμ 对应的特征向量，则平面对≡x = 0, i =1,2在原始坐标系下的方程为

1.4.3 计算步骤

（1） 选择对应的二次曲线对

第一步 对于每一对二次曲线 iC 和 jC′，组成 锥 面 A = PTCiP 和 B = P ′TCiP ′，计 算I2, I3,I4和 Δi,j；

第二步 在两幅图像所有可能的二次曲线 对中选择 ji,Δ 绝对值最小的像对作为可能对应的 二次曲线对；

（2） 射影重建

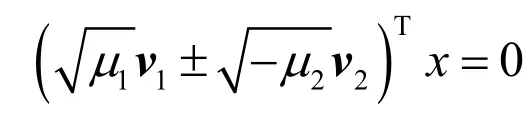
2 实验验证

在本文实验中，使用双目成像获得杯子和盘子的两幅图像，如图1 所示。

实验中的物体共有三条二次曲线，分别是杯子的杯口圆、盘子的外圆和内圆。首先对原始图像进行边缘检测和二次曲线的匹配，匹配后的二次曲线见图2。

图1 实验中的原始图像

图2 图像中的三条二次曲线的匹配

对于两幅图像中的每一对二次曲线计算Δ，计算结果见表1。

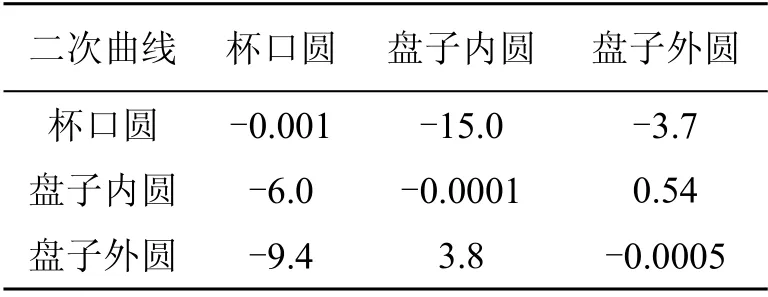
表1 计算两幅图像中的每一对二次曲线Δ

空间二次曲线重建结果见表2。

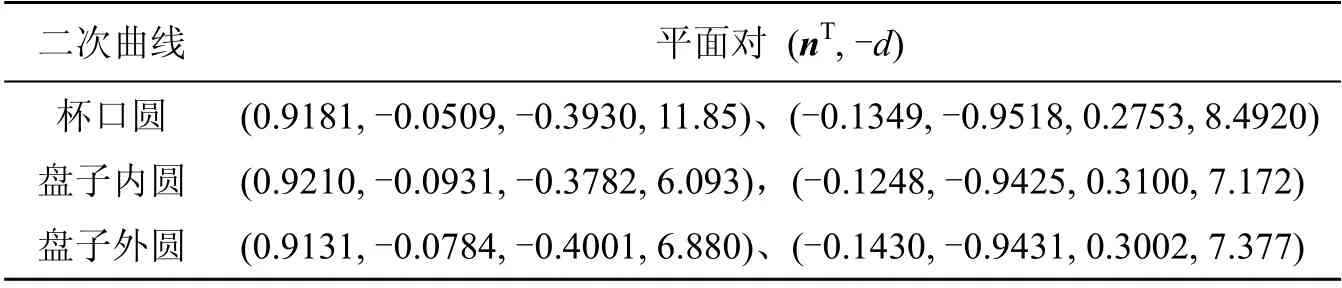
表2 空间二次曲线的重建

利用本文中的计算方法求出了空间二次曲线所在的平面对，而实际杯口圆、盘子内圆、盘子外圆所在的平面是计算结果中平面对中的第一个平面，具体判断还要利用其它条件，在此不再深入讨论。

通过对实验结果的分析可知，杯口圆和盘子外圆高度差是4.97cm，盘子外圆与内圆的高度差是0.787cm；实际通过测量，杯口圆、盘子外圆、盘子内圆距地面的高度分别是8.5cm、3.0cm、2.3cm，也就是说杯口圆和盘子外圆实际高度差是5cm，盘子外圆与内圆的实际高度差是0.7cm，所以计算结果和实际相符。

3 结 论

[1] Luong Q T, Faugeras O D. Self-calibration of a moving camera from point correspondences and fundamental matrices [J]. International Journal of Computer Vision, 1997, 22(3)： 261-289.

[2] Cordelia Schmid, Andrew Zisserman. The geometry and matching of lines and curves over multiple views [J]. International Journal of Computer Vision, 2000, 40(3)： 199-233.

[3] Lasenby J, Fitzgerald W J, Lasenby A N, et al. New geometric methods for computer vision： an application to structure and motion estimation [J]. International Journal of Computer Vision, 1998, 26(3)： 191-213.

[4] Carsten Rother, Stefan Carlsson. Linear multi view reconstruction and camera recovery using a reference plane [J]. International Journal of Computer Vision, 2002, 49(2/3)： 117-141.

[5] Yi Ma. A differential geometric approach to multiple view geometry in spaces of constant curvature [J]. International Journal of Computer Vision, 2004, 58(1)： 37-53.

[6] 储 珺, 高满屯, 陈 震. 从序列图像计算二次曲线的光流[J]. 工程图学学报, 2002, 23(2)： 82-88.

[7] 钟 集, 唐素兰, 叶木秀. 高等几何[M]. 武汉： 武汉大学出版社, 2005. 167-179.