考虑物理特征的避障路径生成算法

罗月童， 王晓静， 瞿德清， 季 浩， 刘晓平

（合肥工业大学计算机与信息学院VCC研究室，安徽 合肥 230009）

路径生成算法是仿真、游戏等领域的重要研究内容，避障路径生成算法是其重要组成部分。文献[1]的算法（如图1 所示）是早期研究工作的一个代表，它首先依据障碍物的凸包确定路径上的关键点，然后用直线依次连接关键点构成避障路径。这种算法不仅所生成的路径不真实，而且它没有考虑运动物体固有的物理属性，如车辆的尺寸、速度、转弯半径等。

本文以车辆为对象，考虑车辆的自身尺寸、速度、转弯、半径等物理属性，提出并实现了一种基于物理模型的避障路径生成算法。

图1 利用直线和障碍物凸包得到路径

1 问题分析

避障路径生成可分为两大步骤：首先按某种规则确定一组关键点，然后采用某种插值算法将所有关键点连接生成一条路径。路径插值算法很多，如文献[1]中线性插值算法、文献[2]中的基于Hermite 样条曲线的路径生成算法。因为，三次参数样条曲线可以经过每一个给定的型值点（路径关键点），给定端点约束条件，便可生成一条C2连续的曲线，且具有几何不变性及局部性等特 点[3-6]，本文基本采用三次参数样条曲线拟合避障路径。因此，问题的关键是确定避障路径的关键点，本文的方法考虑以下因素：

· 障 碍 物 本文仅考虑障碍物的尺寸和形状属性；

· 运动车辆 本文考虑车辆尺寸属性和转弯半径属性；

· 原有路径 为了保证避障路径和原路径之间的G1连续性，本文方法在确定避障路径关键点时需要考虑原有路径的属性。

2 避障路径生成算法

避障路径生成过程如图2 所示，首先需要根据某些条件来确定路径关键点；对于给定的n 个关键点，只要知道各关键点处的空间坐标和边界条件，就可以计算得出各点处的切向量[5]，进而得到各Hermite 曲线段的边界条件，最终插值得到整个样条曲线，即生成路径。

图2 避障算法流程

2.1 确定路径关键点

作为算法的基础，考虑到车辆的尺寸和障碍物尺寸等因素，本文提出了外扩凸包的概念：设车辆的宽度为w，由障碍物凸包的各顶点，分别沿各自两条邻边的外角平分线方向向外扩展k 的距离(k＞w)，所形成的新的凸包多边形，即为外扩凸包，其中k 为外扩系数。本文首先生成障碍物的外扩凸包，然后基于外扩凸包的顶点确定路径关键点。

如图3 所示，假设障碍物存在于原路径L1上 pa、 pb之间。因为，避障路径只能位于原路径的同一侧，因此在生成一条避障路径时，只需考虑位于原路径一侧的外扩凸包顶点，现将位于L1的某一侧的顶点记为 p1… pn。

如果将 p1… pn全作为路径关键点，则生成的路径如图3 中路径L2，过于弯曲，不符合实际。本文按下述方法对 p1… pn进行挑选，使得所生成路径如L3所示，更加自然逼真。

以 pa点为原点，以原路径L1在 pa的切向量方向为x 轴正向建立局部坐标系。设原路径L1的曲线方程为 f ( x,y)=0，分别从 pa, pb向障碍物外扩凸包的各顶点引切线，可得切线斜率kia和 kib, 其中1≤i ≤ n 。显然，无论凸包形状如何，都会存在这样的两个点 ps和pt，它们在原路径曲线的同一侧， ps先于或等于 pt且斜率ksa, ktb的绝对值分别为最大。即满足下面条件：

（1） s ≤ t；

（2） f ( xs,ys)⋅ f(xt,yt)＞0；

将 ps、 pt两点选入控制点集，若它们之间存在其它点 pj,s ≤ j ≤ t，由凸包性可知，其一定在 ts pp 连线的外侧（远离障碍物的一侧），则 加入控制点集，直到控制点集为最大。依次以这些控制点为关键点，可以生成一条样条曲线路径。

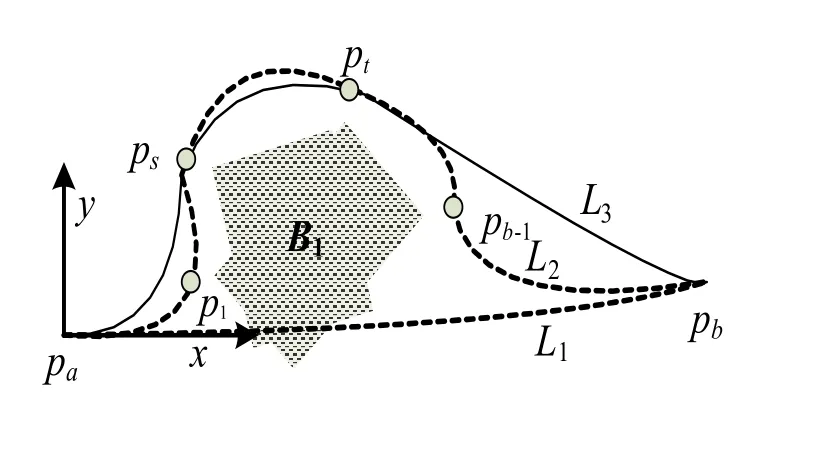
图3 路径关键点的选择

2.2 生成候选路径

为了保证与原路径的G1连续，本文以新路径与原路径连接点处的切向量 p'a、 p'b作为边界条件，可以得到矩阵表达式[5]

从而得到各Hermite 曲线段的端点约束，即得到样条曲线路径。

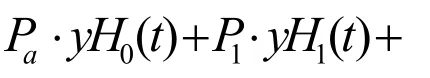
三次Bézier 曲线需要4 个控制点，因为三次参数样条曲线具有几何不变性和局部性，本文用如下方法来确定控制点（如图4 所示）：

图4 第一段曲线的改进

（1） 局部坐标系的建立同2.1；

（3） 依次以 Pa、 A1、 A2、Ps为控制点，形成控制多边形，则生成的Bézier 曲线不会超出控制多边形的区域。

由Bézier 曲线的端点性质可知， Pa、 Ps两点处的切向量方向不会发生变化，故可以保证路径的G1连续。bp 点可用同样方法处理。

2.3 确定避障路径

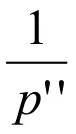
该算法未考虑避障路径上存在障碍物的情况，针对该情况，可以将新障碍物的外扩凸包顶点加入到预选顶点中来，然后再应用该算法，找出避障路径。

3 实验和应用

本算法在某军的三维战场仿真决策系统中得到应用，如图5 所示。图中原路径C1上存在障碍物，C2为避障路径，仿真效果良好。

4 总结与展望

本算法在基于物理模型的基础上，利用三次参数样条曲线生成避障路径，可以保证新生成路径本身的C2连续性和与原路径的G1连续；在计算插值点三维坐标时，只关心车辆的x 和y 坐标，至于车辆的高度信息（z 坐标值），可以在具体的应用中实时获取地面信息，保证车辆随时紧贴地面运动即可；障碍物位于pa, pb中点位置附近时，避障路径生成效果最好，所以本算法与合适的障碍物检测算法配合能达到较好的仿真效果。

[1] 吴风光, 丛 爽. 自动避障中的一种路径生成、选择与实现[C]//自动化理论、技术与应用. 2002： 63-68.

[2] 刘晓平, 曹 力, 张 静. 物体运动路线多样化模拟[J]. 工程图学学报, 2007, 28(3)： 39-43.

[3] 包 晔. 样条插值在运动模拟中的应用[J]. 杭州师范学院学报(自然科学版), 2004, 3(5)： 373-377.

[4] 赖舜男, 吴学礼, 汪国平. G2三次Hermite 样条曲线形状的交互修改[J]. 计算机应用研究, 2004, (10)： 106-109.

[5] 唐泽圣, 周嘉玉, 李新友. 计算机图形学基础[M]. 北京： 清华大学出版社, 1995. 78-87.

[6] 银红霞, 杜四春, 蔡力军. 计算机图形学[M]. 北京：中国水利水电出版社, 2005. 130-159.