创新推理中的物元网络表示法
2010-01-01唐益明刘晓平
唐益明, 刘晓平
(合肥工业大学计算机与信息学院可视化与协同计算(VCC)研究室,安徽 合肥 230009)
在当今激烈的市场竞争中,各个厂家谁能获得更具创新性的产品,谁就能在市场竞争中发展壮大,因此创新推理是制造业在市场竞争中取胜的关键。就产品设计的过程而言,产品设计划分为需求分析、概念设计、详细设计几个阶段,其中集中体现创新推理的阶段是概念设计阶段[1]。研究表明,一个产品的概念设计已决定了从设计到生产该产品所有费用的75%[2]。当前,如何在产品概念设计阶段快速地产生有竞争力的新概念,实现快速的创新推理是设计领域的前沿课题,又是工业界希望尽快运用的成果[3]。
Pahl,Beitz于1984年在经典著作《Engineering Design》一书中指出概念设计的主要过程是:建立功能的结构,并将功能分解为子功能的组合,寻求恰当的设计原理分别去满足这些子功能,然后选择合适的满足总功能的原理组合,最后进行评价选择得到较好的设计概念[4]。其中,拟定功能的结构、进行功能分解、子功能求解与组合等事实上都涉及到功能模型的建立(即功能表示)与创新推理问题[5-6]。如果在前期阶段功能表示不合理,不仅不能准确恰当地表达设计需求,而且难以进行有效地创新推理,甚至可能直接导致概念设计的失败。因此,如何建立恰当的功能模型,并在此基础上进行创新推理就成为了当前概念设计中的关键问题。本文在分析人工智能的知识表示方法、相关改进的功能表示方法、物元表示法等方法的基础上,将语义网络法的思想引入到物元表示法中,提出一种新的功能模型——物元网络,在此基础上提出物元网络法及其创新推理机制,并通过与物元表示法和语义网络法的对比,表明物元网络法能更有效地进行功能表示与创新推理。
1 相关工作
由于创新推理本身属于人工智能领域,因此在功能表示问题上,可考虑利用人工智能领域的知识表示方法,常用的有语义网络表示法、框架法、谓词法、产生式法等。由创新推理的特点,在设计中主要使用的是语义网络法和框架表示法这两种结构化的表示方法[7]。但是,语义网络法、框架表示法本身存在固有的不足,而且这些方法不是专用于创新推理的方法,导致无论是与创新推理的衔接,还是直接进行创新推理,都存在着不足。
传统的知识表示方法在表示功能模型方面存在缺点,不能满足人们进行创新推理的要求,国内外的学者都在改进功能表示方法方面开展了一定的工作。悉尼大学的Qian通过对功能―行为―结构的表达[8],进行产品的拓扑结构设计,并由交互方式在领域内产生新的拓扑方案;美国密西根大学的Chiou等提出了将机构归纳分类[9],构建机构矩阵,实现机构拓扑设计自动化的方法;东京大学的Umeda等以人的认知模型为基础,采用功能―行为―状态的表达方法[10],将功能的分解转化为行为描述的分解,使之符合人的思维活动,此行为描述模型以人的设计思维活动为立足点,有利于功能模型的创新推理。虽然,改进的功能表示方法在解决功能和载体的对应问题上有了一定的进展,但就其概念而言,主要从概念的内涵来表示功能模型,而忽略或隐含概念外延的表示。因此,在处理主要涉及内涵的领域,如诊断与识别时,表现不错,但用于同时需要考虑内涵与外延的领域,如产品设计与企业经营等,就表现得力不从心。
可拓学[11-12]是一门针对创新推理的科学,研究解决矛盾问题的规律和方法,它以物元理论与可拓逻辑为支柱,试图把人们解决问题的过程形式化,从而建立起相应的数学模型, 并在这个基础上发展新的计算方法和技术。可拓学中的知识是用物元来进行表示的,在文献[7]中利用物元表示法进行创新推理,发现与语义网络法、框架法相比,在创新解的数量上有较大程度的提升。但是,进一步研究,发现其推理效率较低。而概念设计本身涉及的数据量往往较大,并且创新的主要难点在于冲突的检测、定位与消解,而求解所得到的庞大的解空间使得设计者很难迅速发现并定位冲突所在,更难以消解冲突[6]。因此,物元表示法推理效率的低下导致难以满足功能模型创新推理的需求,如何提升其推理效率就成了不可回避的问题。
考察物元表示法,发现虽然物元之间有相等、蕴涵、相关和无关等关系,但只能通过物元的可拓性来对某一个具体的物元进行变换得到与其他的物元的相互关系,物元表示法的结构性差是导致推理效率低下的关键因素。而语义网络法是面向知识结构性的,而且在展现设计变量之间的关系、启发设计思维方面拥有独特的优势,因此这里将物元表示法和语义网络法进行结合,提出物元网络表示法。
2 物元网络表示法
2.1 物元网络法的定义
定义1 物元:给定事物的名称N ,它关于特征c 的量值v,以有序三元组( , , )N c v 作为描述事物的基本元,简称物元,记为R。一个事物有多个特征,如果事物N 以n 个特征 c1, … , cn和相 应 的 量 值 v1, … , vn描 述, 则 表 示 为R = [ R1, … , Rn]T(其中 AT表示矩阵A 的转置), 这 时 称R 为n 维 物 元, 简 记 为R = ( N , C, V )。并称 Ri=( N , ci, vi)( i = 1,2,… ,n)为R 的分物元。物元全体构成的集合记为ℜ。
对于物元之间的关系,可定义2 个算子。具体表示如下:
定义2 可拓变换算子集合 Ω = {ϕth,ϕch, ϕvl,ϕex,ϕcj,ϕre, …}(集合内元素依次分别表示:同物,同征,同值,可扩,共轭,相关等),若 R1,R2∈ℜ, ∃ϕ ∈Ω,使得 ϕ( R1)= R2,则记 R1├ΩR2。
语义网络表示法中的关系主要有实例,泛化,聚集,属性4种。其中,聚集和属性可用物元表示的三元组表示,实例和泛化如用三元组表示则不太方便,可直接用语义网络中的弧表示之间的关系。因此有:
定义3 语义网络算子集合 Σ = {ϕin,ϕge} (集合内元素依次分别表示:实例,泛化),若R1, R2∈ℜ, ∃ϕ ∈Σ,使得 ϕ( R1)= R2,则记
R1├ΣR2。
可拓变换算子基于可拓学理论,籍此可对物元进行可拓变换。通过对物元的三元组变量进行变换,可以找出与原物元结点相关的其它结点。而语义网络算子则是建立物元的实例与类、类与类结点之间的关系。如果单纯地应用物元方法,则需要建立专门的三元组来表示这类关系,但通过使用语义网络的弧,不仅简化了物元的个数,还显示出物元之间存在的结构关系,使得物元之间的相互关系更加清晰。根据上面物元的定义和相关算子的定义,可以得到一种新的功能模型——物元网络,定义如下:
定义4 定义物元网络为 G = (V , E ,φ),其中:① V (G ) ={R1, … , Rn}⊆ℜ, V ( G)≠∅;② E( G ) = {e1,… , em} ,其中 ei∈Σ ∪Ω ,(i =1,… , m); ③ φ( G ):E →V × V,其中φ ( e) =< R1,R2>当且仅当 R1├ΣR2或 R1├ΩR2,且e 为以 R1为起点、 R2为终点的有向边。(其中e ∈ E,R1, R2∈ V)。称用物元网络进行表示的方法为物元网络表示法,简称物元网络法。
2.2 物元网络法的创新推理
由定义4 可知:物元结点之间的变换主要是通过可拓变换算子和语义网络算子进行的。语义网络变换主要是显示功能模型的物元之间结构关系,而对物元进行扩展主要依靠的是可拓变换(即基于可拓变换算子的变换)。

定理1 设ℜ 有限,则存在一个确定的最小自然数m 满足: Wh( R ) = Wm( R)。
证 明由于ℜ 有限,则 W1( R ), W2( R ),…均有限,且 W1( R ) ⊂ W2( R)⊂…,并且均满足Wi( R )⊂ℜ( i= 1,2,…)。必定存在自然数m 满足 Wm+1( R) = Wm( R),且 Wm( R ) − Wm−1( R)≠∅。事实上, 如果任意自然数k 均满足Wk( R ) − Wk−1( R)≠∅,则随着k 的不断增大,必然存在k 使 Wk( R )不包含于ℜ,出现矛盾。由定义5:Wm+j( R ) = Wm( R)( j= 1,2,…),则Wh( R) =nl→im+∞Wn( R ) = Wm( R)(m 显然最小)。
证毕。
定理2 Wn( R) =∪R′∈W1(R)Wn−1( R′)( n≥2)。
证 明Wn( R ) =∪R′∈Wn−1(R)W1( R′),而由定义5 易知:∪R′∈Wn−1(R)W1( R′ )=∪R′∈Wn−2(R)W2( R′), 则 Wn( R ) =∪R′∈Wn−2(R)W2( R′),因此类推可得:Wn( R ) =∪R′∈W1(R)Wn−1( R′)。证毕。
推论1 Wn( R ) =∪R′∈Wn−1(R)W1( R′)= ∪R′∈Wn−2(R)W2( R′ )= …=∪R′∈W1(R)Wn−1( R′)。
功能物元R的全创新空间 ( )Wh R 一般很大, 对于所研究的某个领域或某种目的来说,可能并不需要全创新空间上的所有信息,因此需要考虑其受到限制的情形。
定义6 设 R = ( N , C ,V )为物元,设其事物、 特征和量值的全体集合依次为{ N },{C } ,{V },分别定义 L ( N ), L (C ), L (V )为事物、特征和量值的限制,其中 L ( N ) ⊂ { N},L( C ) ⊂ {C },L (V ) ⊂ {V }。记 L =( L ( N ), L ( C), L (V )),称R 在限制L 下可得到的全创新空间为R 的L −受限全创新空间 W hL( R )。
以下定理3 是显然的:
定理3 W hL(R ) = WhLN( R ) ∩ WhLC( R)∩ WhLV( R ),其中 LN=( L ( N ),{ C },{V }),LC=({N }, L(C ),{V }), LV=({N } ,{C } , L( V ))。
这样在设计过程中,使得相关功能模型信息 的求解空间从原先的R 扩展到了 ( )Wh R ,从而 扩大了求解空间的范围,为设计者提供了更多的与设计问题相关的信息,辅助设计者获得更多的求解思路,从而更加有利于设计者获得创新的设计解。
3 实验及理论分析
为了进行知识表示方式的比较,这里依然采用文献[7]中的菜谱原型系统的知识库,对其分别 就语义网络法、物元表示法、物元网络法进行了实验对比。首先对一定数量的菜谱采用不同的知识表示方法,建立数据库。每道菜由主料、佐料、烹饪方法和口味4 个关键字组成。然后,建立了关于菜谱的创新推理的一个原型系统。当用户提出某种口味要求后,系统首先根据匹配找出符合要求的已有菜谱。然后,根据正向推理方法,利用分解和组合,对数据库中相关口味的菜谱进行推理,提出新的主料、佐料、烹饪方法和口味的组合,从而产生新的菜谱。
(1) 数据库大小
从表1 可以看到语义网络法所要用的表单数量最多,而物元法所用的表单数量最少,这是因为,物元法只需要存储各种不同的物元,而物元间的相互关系则蕴含在物元的各属性间。而语义网络法不仅要表示各种节点的信息,还要表示各节点之间的关系,所以所用表单数量也就最多。物元网络法由于是在物元表示法的基础上添加了实例与泛化的关系,所以表单数比物元法要多,但添加表单的数量还是要远远少于语义网络法的表单数。

表1 数据库比较表
由于物元法和物元网络法的本质是一样的,所以相对存储空间基本相同,但由于物元网络法添加了物元之间的可拓关系和语义关系,所以就记录条数而言,物元网络法与语义网络法较单纯的物元法要多。
(2) 数据结论的比较
基于不同的知识表示方法的数据库,在相同的推理机制下,选择相同的口味,通过推理所得到的结果差别也是比较大的,如图1 所示。
由于是创新推理,所以希望在固定的数据库中,通过相同的推理方法,得到的结果越多越好。结果越多,说明推理中发现的隐含知识就越多,从而得到的可用的创新结果的几率也就越大。由图1 可知,从所得到的结果的数量上来看,物元表示法和物元网络法的结果数基本相同,但较语义网络法所得到的结果要多。从具体得到的结果看,后两种方法的结果也是相同的,而语义网络法得到的结果是后两种的子集。造成这种方法的原因是:物元网络法只是将物元法中的实例和泛化关系以弧的形式进行了表示,使得功能模型的结构关系更加明显,但从本质上来说后两种方法是相同的,从而使得他们的结果的数量和具体内容都比较相似。而物元表示法和物元网络法在推理过程中,可有效的搜索到一些隐含的知识,就相当于无形中扩大了数据库中的存储数量,从而所得到的结果要多于语义网络法,且结果中也包含了第一种方法的结果。
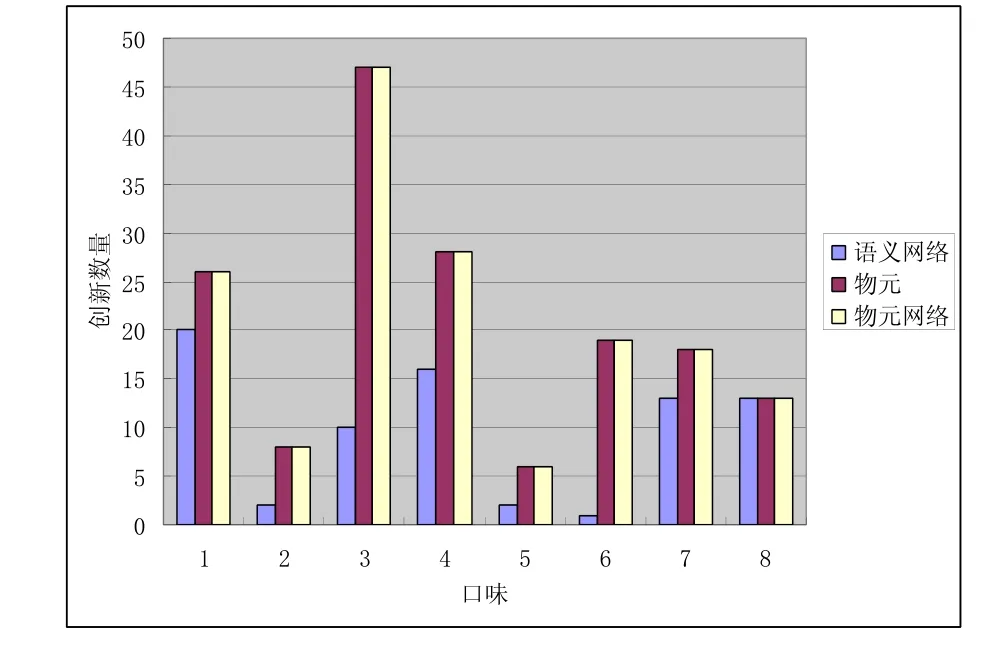
图1 推理结果数量比较
(3) 数据库的可扩充性比较
数据库好坏的一个重要的指标是数据库的可扩充性。语义网络知识表示的定义就决定了基于语义网络法的数据库扩充的复杂性。如要进行知识的扩充,需要对输入项进行分析,画出其关系的网络结构图,然后对数据库中所有与新知识有关的知识进行修改,这样将大大增加数据库的维护成本,尤其对于大型的数据库,这将是一个巨大的工程。但物元表示法和物元网络法相对于语义网络法要简单许多,只要根据特征值,就可以将知识方便地添加到数据库中,非常有利于数据库的扩充。
(4) 运行时间比较
通过具体的统计,可以得到运用不同的表示方法在具体的推理过程中所花费时间的比较,如图2 所示。
从图2 中,可以看出,物元法和物元网络法较语义网络法所用的时间多,这是因为语义网络法不能对推理过程中的信息进行扩展,所以相对的推理所花时间是最少的。而物元网络法比单纯的物元法要多出物元之间的一些结构化的信息,而不需要单纯地凭借属性及属性值的相互关系进行推理,所以所花的时间较其要少。但由所得的结论和所花的时间的比值,可以得到不同知识表示方法的推理效率如图3 所示,一般来说物元网络法所获得单个结论所花时间是最少的,即物元网络法的推理效率是最高的。
由上面的分析及具体的实验数据,总结起来如表2。可以发现,物元网络法综合了物元表示法和语义网络两者的优点,既具备了一定的结构性,还保证了一定的联想性,在基于功能的概念设计过程中,能够很好的对功能模型进行表示,同时可以利于设计者更加方便地寻找类似的信息,具有更好的效果。

图2 运行时间比较图
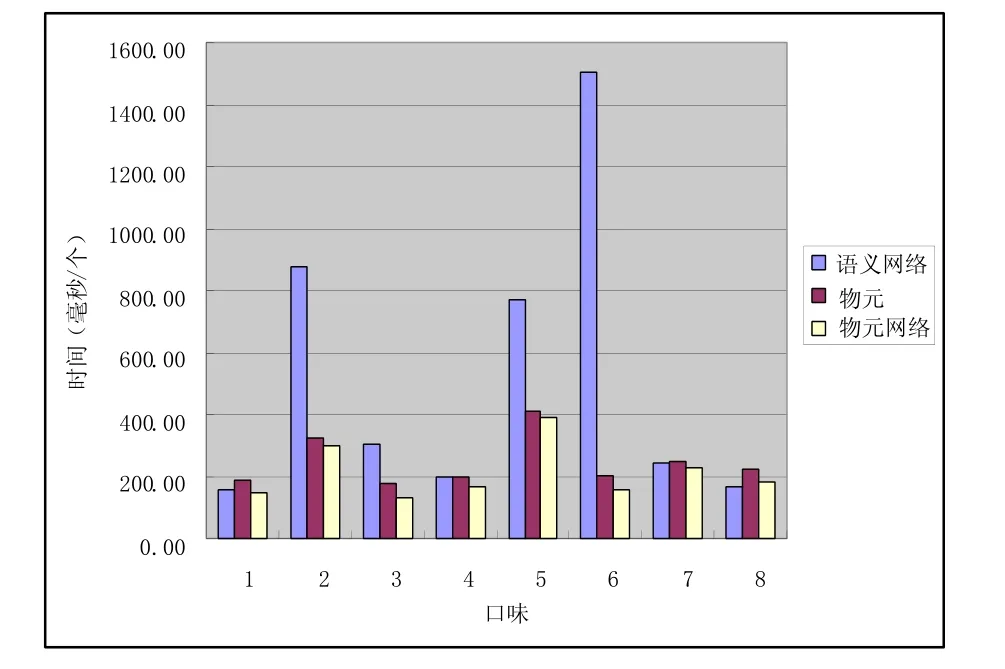
图3 推理效率图

表2 总体比较
4 总结与展望
物元网络法是结合了语义网络法和物元法之后形成的一种新的知识表示方法,其特点主要有:
(1) 物元网络法以物元为节点,以语义网络中的实例和泛化为弧。这样不仅克服了语义网络法中节点信息混乱的缺点,还使得物元之间的关系形成了结构化,从而使得关系更加清晰;
(2) 物元网络法通过可拓变换算子,可以对节点信息进行扩展。从而使得设计者在设计过程中可以得到节点启发性信息的驱动;
(3) 物元网络法是一种可以区别产品的“与”“或”信息的面向对象的知识表示方法。但它比传统的面向对象的知识表示方法的表示能力更强,刻画了产品间丰富的天然联系;
(4) 物元网络法可利用可拓学的创新思维过程,包括矛盾模型化和矛盾解决的过程。
物元网络法有较丰富的推理。除了网络中本身的推理外,还可以通过物元的可拓性,增加推理的元素。同时,由于结点是一个个的物元,可以通过可拓学的推理规则,来进行推理。由此可见,物元网络法较单纯的语义网络法或者物元法,在功能模型的表示方法和创新推理途径上都得到了增强。
[1] Tang Yiming, Liu Xiaoping. Task partition for function tree according to innovative functional reasoning [C]//Proceedings of the 2008 12th International Conference on Computer Supported Cooperative Work in Design (CSCWD'2008). Xi’an, China, IEEE Press, 2008: 189-195.
[2] Hsu W, Liu B. Conceptual design: issues and challenges [J]. Computer-Aided Design, 2000, 32(14): 849-850.
[3] 檀润华, 王庆禹, 苑彩云, 等. 发明问题解决理论:TRIZ——TRIZ 过程、工具及发展趋势[J]. 机械设计, 2001, (7): 7-12.
[4] Pahl G, Beitz W. Engineering design [M]. London: The Design Council, 1984. 57.
[5] Amaresh Chakrabarti, Thomas P Bligh. A scheme for functional reasoning in conceptual design [J]. Design Studies, 2001, 22(6): 493-517.
[6] 刘晓平, 唐益明, 秦 晋, 等. 概念设计中基于扩展功能矩阵的功能求解方法[J]. 计算机辅助设计与图形学学报, 2007, 19(12): 1610-1617.
[7] 刘晓平, 秦 晋. 创新设计中的物元的知识表示方法[J]. 工程图学学报, 2006, 27(6): 31-35.
[8] Qian L, Gero J S. Function-behavior-structure paths and their role in analogy-based design [J]. Artificial Intelligence in Engineering Design, Analysis and Manufacturing, 1996, 10(4): 289-312.
[9] Shean-Juinn Chiou, Sridhar Kota. Automated conceptual design of mechanisms [J]. Mechanism and Machine Theory, 1999, 34: 467-495.
[10] Umeda Y, Ishii M, Yoshioka M, et al. Supporting conceptual design base on the function-behavior-state modeler [J]. Artificial Inteligence for Engineering Design, Analysis and Manufacturing, 1996, 10(4): 275-288.
[11] 刘晓平, 李书杰, 秦 晋. 基于可拓学的产品功能创新模型[J]. 工程图学学报, 2007, 28(4): 12-16.
[12] Liu Xiaoping, Qin Jin, Tang Yiming. An innovative function-tree building method based on similarity theory and extension theory [C]//Proceeding of CAID&CD’06, Hangzhou, China, 2006: 199-204.
