运用“几何画板”进行数学实验

黄勇彬

“几何画板”能迅速准确地画出各种图形和各类函数的图像，能方便地让图形运动、变化、拆分、转换，能用参数控制曲线……这些功能改变了研究数学只用纸和笔的传统方式。它丰富和发展了“数学实验”的内涵，为数学实验教学的开展提供了有效的手段和良好的工具。特别是利用“几何画板”做实验，可使我们从起始的混乱中观察、捉摸有规则的结构，这是数学灵感和数学发现的源泉，也是数学研究的有效方法。下面阐述利用“几何画板”来进行数学实验的意义。

一、运用“几何画板”进行数学实验是开展探究式教学的需要

在探究式教学中，对复杂而抽象的图象、图形进行研究，如果只靠传统的笔、纸是很难开展的，而利用“几何画板”设计数学实验能够帮助学生在动态中观察、探索、发现数学规律和结论，丰富探究的内涵。

例一：“函数y=A sin(ωx+ψ)的图象”一课。通过观察计算机给出的动态变化图象知道，对于给定的三角函数关系式，x取某个区间的值时，图象就被确定在某个位置，从而找出函数表达式所对应的函数图象。教师事先用“几何画板”等软件制作好课件，上课时学生上机实验。

这一节课的教学设计可分为几个环节。第一个环节是让学生观察函数y=A sin(x)的图象，通过改变A，观察函数图象的变化，记录纵坐标的变化。第二个环节是让学生观察函数y=sin(ωx)的图象，通过改变ω，观察函数图象的变化，记录横坐标的变化。第三个环节是让学生观察函数y=sin(x+ψ)的图象，通过改变ψ，观察函数图象的变化，记录图象的平移变化。第四个环节是让学生通过小组讨论，利用计算机得出函数y=A sin(ωx+ψ)的图象，总结变化规律。学生基于对实验现象的观察提出猜想，小组代表作口头回答，学生发表意见，老师给予评价，从而成功完成“函数y=A sin(ωx+ψ)的图象”一节的教学。

实验使学生实现从“听数学”到“做数学”的转变，学生作为研究者，参与包括发现、探索在内的获得知识的全过程。

二、利用“几何画板”进行数学实验，有助于学生理解与掌握数学结论

运用“几何画板”的动态数据更新与动态图形变换功能，可使实验者能直观地看到数学结论的形成过程，从而能促进对其理解和掌握。

例二：对数函数的图象和性质教学。传统教学由于受手段限制，对函数y=log_ax的图象随着底数。的变化而变化，只能用特例来说明。通常都是通过比较y=log₂x、y=log₃x、y=log_1/2x、y=log_1/3的图象总结出一般结论，学生会有点以偏代全的感觉。学生对为什么要把底数a分为01两种情加以讨论不一定理解，学习过程比较被动。为解决这个问题，可使用“几何画板”做这样的实验研究：

先引导学生用“几何画板”作出以动点A的纵坐标作为底数的函数y=log_ax的图象，通过拖动点A，改变底数a，观察函数y=log_ax的图象随着底数的改变而变化。在此过程中，学生可清楚地看到底数。如何影响并决定着函数y=log_az的性质。由于函数的图象随着a在01这两个区间自然聚集，学生可以清楚地看到a=1是一条分界线，而对函数的定义域、值域、单调性、特殊点(1，0)等更是一目了然。还可以把点A拖到x轴上方和x轴下方，让底数a为零和负数，观察图象如何变化。

实验充分地向学生展示了“为什么要求底数a>0且a≠1”和“过点(1，0)为什么要作为性质之一”等，让学生理解了有关数学结论的形成。

三、利用“几何画板”进行数学实验。能激发创造意识和创新欲望

亚里士多德说过：“思维从对问题的惊讶开始。”使用“几何画板”做实验，可以创设一些传统教学手段难以模拟的问题情境，使学生产生这种“惊讶”，在教学内容和学生求知心理之间创造一种“不协调”，从而激发学生的好奇心，增强他们的求知欲。

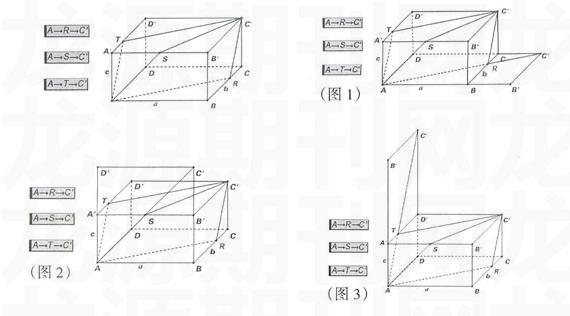
例三：问题“有一个长为a，宽为6，高为c的房子(a>b>c)，一只蚂蚁要从地面的角落A爬到对面天花板的角落c'，选择怎样的路线能使得爬行距离最短?”

由于A点到c点的空间路线要经过几个平面，每个平面的路线又有不确定性，从而增加了问题的复杂性，致使学生思路受阻。(如下图)

用“几何画板”设计出长、宽、高三个方向的展开图，让学生分别计算蚂蚁按路线A→R→C(图1)、路线A→s→c(图2)、路线A→T→C(图3)爬行时的最短距离是多少，从而得出从A到c的最短距离方案。

利用“几何画板”开展数学实验的意义，不仅在于使学生掌握必要的数学知识，更重要的是在于提高学生学习数学的积极性和数学应用意识，培养了学生独立思考的学习品质和探索精神，提高了学生分析和解决问题的能力。